tailieuviet.vn giới thiệu Giải bài tập Toán 9 Bài 1: Căn bậc hai chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9
a) 9; b) 49; c) 0,25; d) 2.
Phương pháp giải:
+ Căn bậc hai của một số a không âm là số x sao cho x2=a.
+ Số dương a có đúng hai căn bậc hai là hai số đối nhau là a và −a.
Lời giải:
+ Căn bậc hai của số 9 là 3 và −3 (vì 32=9 và (−3)2=9)
+ Căn bậc hai của số 49 là 23 và −23 (vì (23)2=49 và (−23)2=49)
+ Căn bậc hai của số 0,25 là 0,5 và −0,5 ( vì 0,52=0,25 và (−0,5)2=0,25)
+ Căn bậc hai của số 2 là 2 và −2 (vì (2)2=2 và (−2)2=2)
Trả lời câu hỏi 2 trang 5 SGK Toán 9 Tập 1: Tìm căn bậc hai số học của mỗi số sau:
a) 49
b) 64
c) 81
d) 1.21
Phương pháp giải:
Ta sử dụng: Nếu {x≥0x2=a thì x=a.
Lời giải:
a) 49=7 vì 7≥0 và 72 = 49
b) 64=8 vì 8≥0 và 82 = 64
c) 81=9 vì 9≥0 và 92 = 81
d) 1,21=1,1 vì 1,1≥0 và 1,12 = 1,21
a) 64
b) 81
c) 1.21
Phương pháp giải:
Căn bậc hai của số a không âm là a và −a
Lời giải:
a) Căn bậc hai của số 64 là 8 và −8
b) Căn bậc hai của số 81 là 9 và −9
c) Căn bậc hai của số 1,21 là 1,1 và −1,1
a) 4 và 15
b) 11 và 3.
Phương pháp giải:
Sử dụng với hai số a;b không âm ta có a<b⇔a<b
Lời giải:
a) Vì 16 > 15 nên 16>15. Vậy 4 > 15
b) Vì 11 > 9 nên 11>9. Vậy 11 > 3
a) x>1
b) x<3
a) Phương pháp giải:
Sử dụng với hai số a;b không âm ta có a>b⇔a>b rồi kết hợp với x không âm để kết luận.
Lời giải:
x>1⇔x>1⇔x>1
Kết hợp với x≥0 ta có x>1 thỏa mãn đề bài.
b) Phương pháp giải:
Sử dụng với hai số a;b không âm ta có a<b⇔a<b rồi kết hợp với x không âm để kết luận.
Lời giải:
x<3⇔x<9⇔x<9
Kết hợp điều kiện x≥0 ta có 0≤x<9
Bài tập ( trang 6-7 ) SGK Toán 9
121; 144; 169; 225; 256; 324; 361; 400.
Phương pháp giải:
+) Căn bậc hai số học của a là a với a>0.
+) Số dương a có đúng hai căn bậc hai là hai số đối nhau: Số dương kí hiệu là a và số âm kí hiệu là −a.
Lời giải:
Ta có:
+ 121 có căn bậc hai số học là 11 (vì 11>0 và 112=121 )
⇒121 có hai căn bậc hai là 11 và −11.
+ 144 có căn bậc hai số học là 12 (vì 12>0 và 122=144 )
⇒144 có hai căn bậc hai là 12 và −12.
+ 169 có căn bậc hai số học là 13 (vì 13>0 và 132=169 )
⇒169 có hai căn bậc hai là 13 và −13.
+ 225 có căn bậc hai số học là 15 (vì 15>0 và 152=225 )
⇒225 có hai căn bậc hai là 15 và −15.
+ 256 có căn bậc hai số học là 16 (vì 16>0 và 162=256 )
⇒256 có hai căn bậc hai là 16 và −16.
+ 324 có căn bậc hai số học là 18 (vì 18>0 và 182=324 )
⇒324 có hai căn bậc hai là 18 và −18.
+ 361 có căn bậc hai số học là 19 (vì 19>0 và 192=361 )
⇒361 có hai căn bậc hai là 19 và −19.
+ 400 có căn bậc hai số học là 20 (vì 20>0 và 202=400 )
⇒400 có hai căn bậc hai là 20 và −20.
Bài 2 trang 6 SGK Toán 9 Tập 1: So sánh
a) 2 và 3
b) 6 và 41
c) 7 và 47
Phương pháp giải:
+) Sử dụng định lí so sánh hai căn bậc hai số học: Với hai số a và b không âm ta có:
a<b⇔a<b
Lời giải :
a) Ta có: 2=4
Vì 4>3⇔4>3⇔2>3.
Vậy 2>3.
b) Ta có: 6=36
Vì 36<41⇔36<41⇔6<41
Vậy 6<41.
c) Ta có: 7=49
Vì 49>47⇔49>47⇔7>47.
Vậy 7>47.
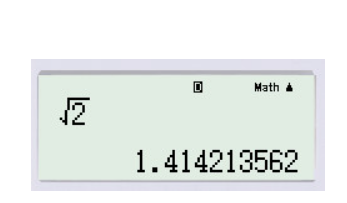
Bài 3 trang 6 SGK Toán 9 Tập 1 :Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau (làm tròn đến chữ số thập phân thứ 3):
a) x2=2
Phương pháp giải:
+) x2=a⇔x=±a, (a≥0 ).
+) Sử dụng quy tắc làm tròn số:
Nếu chữ số đầu tiên bỏ đi nhỏ hơn 5 thì ta giữ nguyên các chữ số còn lại.
Nếu chữ số đầu tiên bỏ đi lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào chữ số cuối cùng của bộ phận còn lại.
Lời giải:
a) Ta có: x2=2⇔x=±2
Bấm máy tính ta được:
x≈±1,414
b) Ta có: x2=3⇔x=±3
Tính bằng máy tính ta được:
x≈±1,732
c) Ta có: x2=3,5⇔x=±3,5
Tính bằng máy tính ta được:
x≈±1,871
d) Ta có: x2=4,12⇔x=±4,12
Tính bằng máy tính ta được:
x≈±2,030
Bài 4 trang 7 SGK Toán 9 Tập 1: Tìm số x không âm, biết:
a) x=15
b) 2x=14
c) x<2
b) Vì x≥0 nên
2x=14⇔x=7
⇔(x)2=72 ⇔x=49
Vậy x=49
c) x<2⇔x<2
Kết hợp với x≥0 ta có 0≤x<2
Vậy 0≤x<2
d) Với x≥0 ta có 2x<4 ⇔2x<16
⇔2x<16 ⇔x<8
Kết hợp điều kiện x≥0 ta có: 0≤x<8
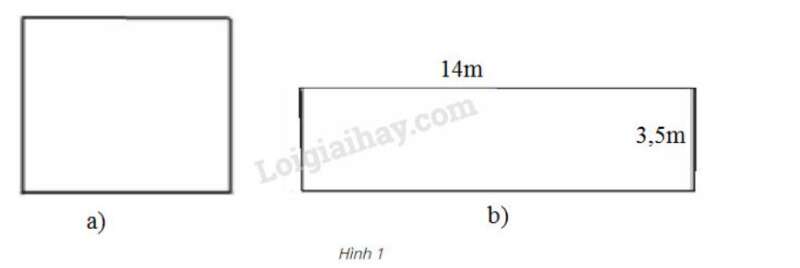
Bài 5 trang 7 SGK Toán 9 Tập 1:Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của một hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.
Phương pháp giải:
– Công thức tính diện tích hình vuông cạnh a là S=a2.
– Công thức tính diện tích hình chữ nhật có chiều dài và chiều rộng lần lượt là a;b là S=a.b
Lời giải:
Gọi x (m) là độ dài hình vuông, x>0 .
Diện tích của hình vuông là: x2(m2)
Diện tích của hình chữ nhật là: 3,5.14=49 m2.
Theo đề bài, diện tích của hình vuông bằng diện tích của hình chữ nhật, nên ta có:
x2=49⇔x=±49⇔x=±7.
Vì x>0 nên x=7.
Vậy độ dài cạnh hình vuông là 7m.
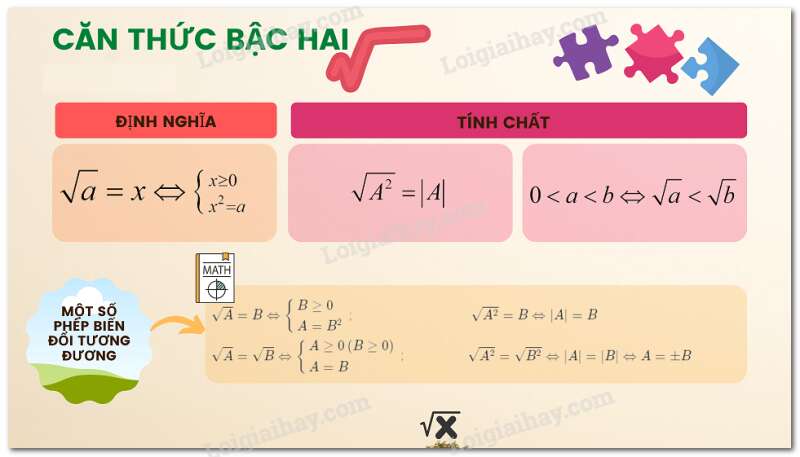
1. Căn thức bậc hai
Căn bậc hai số học
Số dương a có đúng hai căn bậc hai là: a và −a
Với số dương a, số a được gọi là căn bậc hai số học của a.
Số 0 cũng được gọi là căn bậc hai số học của 0.
+) a=x⇔{x≥0x2=a
+) So sánh hai căn bậc hai số học:
Với hai số a,b không âm ta có a<b⇔a<b.
Căn thức bậc hai
Với A là một biểu thức đại số, người ta gọi A là căn thức bậc hai của A. Khi đó, A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
A xác định hay có nghĩa khi A lấy giá trị không âm.
Chú ý.:
Với a≥0, ta có:
+ Nếu x=a thì {x≥0x2=a
+ Nếu {x≥0x2=a thì x=a.
Ta viết x=a⇔{x≥0x2=a
2. So sánh các căn bậc hai số học
ĐỊNH LÍ:
Với hai số a;b không âm ta có a<b⇔a<b
Ví dụ: So sánh 3 và 7
Ta có: 3=9 mà 9>7 suy ra 9>7 hay 3>7
Hằng đẳng thức A2=|A|
Với mọi số a, ta có a2=|a|.
Một cách tổng quát, với A là một biểu thức ta có
A2=|A| nghĩa là
A2=A nếu A≥0 và A2=−A nếu A<0.
3. Một số dạng toán thường gặp
Dạng 1: Tìm căn bậc hai số học và so sánh hai căn bậc hai.
Phương pháp:
Sử dụng kiến thức với hai số a,b không âm ta có a<b⇔a<b.
Dạng 2: Tính giá trị của biểu thức chứa căn bậc hai
Phương pháp:
Sử dụng hằng đẳng thức A2=|A|={AkhiA≥0−AkhiA<0
Dạng 3: Rút gọn biểu thức chứa căn bậc hai
Phương pháp:
– Đưa các biểu thức dưới dấu căn về hằng đẳng thức (thông thường là (a+b)2=a2+2ab+b2, (a−b)2=a2−2ab+b2)
– Sử dụng hằng đẳng thức A2=|A|={AkhiA≥0−AkhiA<0
Dạng 4: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa
Phương pháp:
Sử dụng kiến thức biểu thức A có nghĩa khi và chỉ khi A≥0.
Dạng 5: Giải phương trình chứa căn bậc hai
Phương pháp:
Ta chú ý một số phép biến đổi tương đương liên quan đến căn thức bậc hai sau đây:
A=B⇔{B≥0A=B2 ; A2=B⇔|A|=B
A=B⇔{A≥0(B≥0)A=B ; A2=B2⇔|A|=|B|⇔A=±B
