SBT Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn | Giải SBT Toán lớp 9 

Sử dụng kiến thức: Cho đường thẳng a và đường tròn (O) với d là khoảng cách từ O đến đường thẳng a

+) Nếu d=R thì đường thẳng a và đường tròn (O) tiếp xúc nhau.

+) Nếu d>R thì đường thẳng a và đường tròn (O) không giao nhau.

Lời giải:

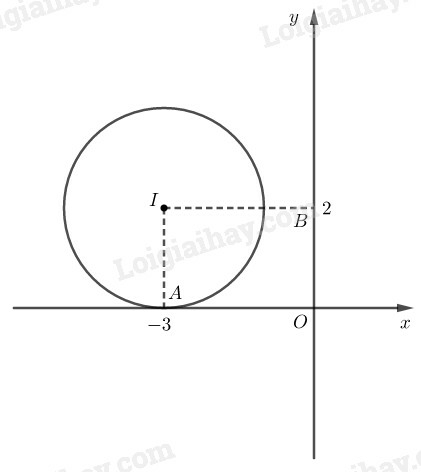
Kẻ IA⊥Ox

Ta có: IA=2=R

Suy ra đường tròn (I) tiếp xúc với trục hành.

Kẻ IB⊥Oy

Ta có: IB=3>R

Suy ra đường tròn và trục tung không có điểm chung.

Sử dụng kiến thức:

+) Tập hợp tất cả những điểm cách đều đường thẳng b một khoảng h cho trước là hai đường thẳng song song với đường thẳng b và các b một khoảng h.

Lời giải:

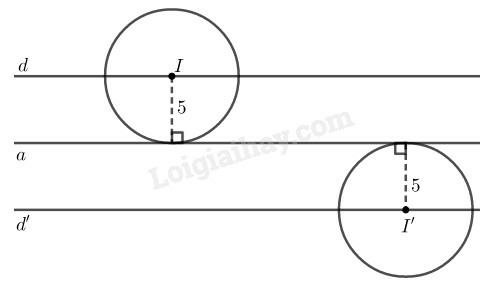
Vì đường tròn tâm I bán kính 5cm tiếp xúc với đường thẳng a nên khoảng cách từ I đến a là 5cm.

Vậy I nằm trên hai đường thẳng d và d′ song song với a, cách a một khoảng bằng 5cm.

a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy.

b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.

Phương pháp giải:

Sử dụng kiến thức: 

Cho đường thẳng a và đường tròn (O) với d là khoảng cách từ O đến đường thẳng a.

+) Nếu d<R thì đường thẳng a và đường tròn (O) cắt nhau.

Sử dụng định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải:

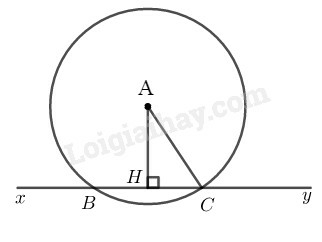
a) Kẻ AH⊥xy

Ta có: AH=12cm

Bán kính đường tròn tâm I là 13cm nên R=13cm.

Mà   AH=d=12cm

Nên suy ra  d<R

Vậy (A;13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C.

b) Áp dụng định lí Py-ta-go vào tam giác vuông AHC, ta có:

AC2=AH2+HC2

Suy ra: HC2=AC2−AH2=132−122=25⇒HC=5(cm)

Xét đường tròn tâm A có AH⊥BC tại H nên H là trung điểm của BC (đường kính vuông góc với dây thì đi qua trung điểm của dây đó)

Suy ra  BC=2.HC=2.5=10(cm)

Sử dụng định nghĩa, tính chất đường trung bình của tam giác: 

+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Lời giải:

Trong tam giác ACD, ta có:

+) B là trung điểm của AC(gt)

+) O là trung điểm của CD

Nên OB là đường trung bình của ∆ACD.

Suy ra: OB=12AD ( tính chất đường trung bình của tam giác)

Vậy AD=2.OB=2.2=4(cm).

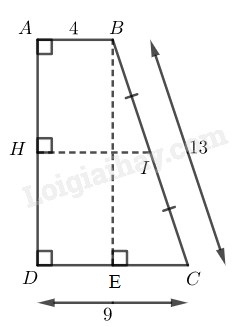
a) Tính độ dài AD. 

b) Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính là BC.

Phương pháp giải:

Sử dung kiến thức:

+) Tứ giác có ba góc vuông là hình chữ nhật.

+) Sử dụng định lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.

+) Nếu d=R thì đường thẳng a và đường tròn (O) tiếp xúc nhau (với d là khoảng cách từ O đến đường thẳng a)

Lời giải:

a) Kẻ BE⊥CD tại E

Suy ra tứ giác ABED là hình hình chữ nhật (vì có ba góc vuông A^=D^=E^=900)

Suy ra AD=BE, DE=AB=4(cm)

Suy ra: CE=CD–DE=9–4=5(cm)

Áp dụng định lí Py-ta-go vào tam giác vuông BCE ta có:

BC2=BE2+CE2

Suy ra: BE2=BC2−CE2=132−52=144

             BE=12(cm)

 Vậy:  AD=12(cm)

b) Gọi I là trung điểm của BC

Ta có: IB=IC=12BC=12.13=6,5(cm)  (1)

Kẻ IH⊥AD.

Xét hình thang ABCD ta có: IH//AB//CD (cùng vuông góc với AD), mà I là trung điểm BC nên H là trung điểm AD.

Khi đó HI là đường trung bình của hình thang ABCD.

Ta có: HI=AB+CD2=4+92=6,5(cm)  (2)

Từ (1) và (2) suy ra: IH=IB=12BC

Vậy đường tròn (I;BC2) tiếp xúc với đường thẳng AD.

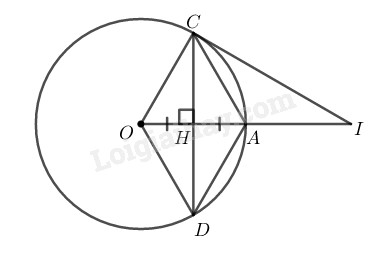
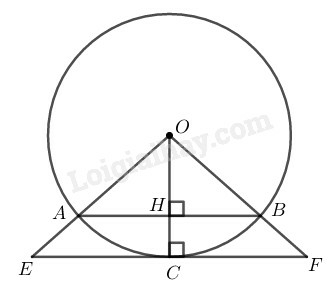
a) Tứ giác OCAD là hình gì ? Vì sao?

b) Kẻ tiếp tuyến đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Tính độ dài CI biết OA=R.

Phương pháp giải:

Sử dụng kiến thức:  

+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

+) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi. 

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

Lời giải:

a) Gọi H là giao điểm của OA và CD

Vì CD là đường trung trực của OA nên:

    CD⊥OA và HA=HO

Xét đường tròn (O) có CD⊥OA tại H nên H là trung điểm của dây CD hay HC=HD (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Vì tứ giác ACOD có hai đường chéo CD và OA cắt nhau tại trung điểm H của mỗi đường nên nó là hình bình hành.

Đồng thời CD⊥OA nên ACOD là hình thoi.

b) Vì ACOD là hình thoi nên AC=OC

Mà OC=OA(=R) nên OA=OC=AC, suy ra tam giác OAC đều.

Suy ra: COA^=60∘ hay COI^=60∘

Mà CI⊥OC (tính chất tiếp tuyến)

Trong tam giác vuông OCI, ta có:

CI=OC.tan⁡COI^=R.tan⁡60∘=R3.

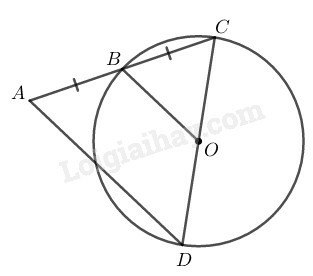
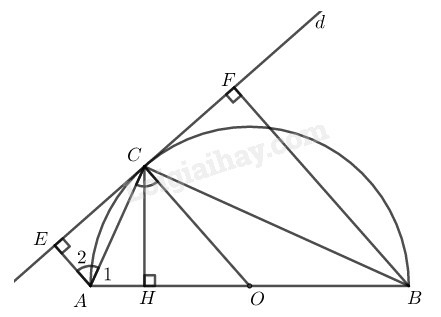
a) CE=CF;

b) AC là tia phân giác của góc BAE;

c)  CH2=AE.BF. 

Phương pháp giải:

Sử dụng kiến thức:

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông lên cạnh huyền.

Lời giải:

a) Ta có: OC⊥d ( tính chất tiếp tuyến)

AE⊥d(gt)

BF⊥d(gt)

Suy ra:  OC//AE//BF(∗)

Mà  OA=OB(=R)

Suy ra: CE=CF (tính chất đường thẳng song cách đều)

b) Ta có: AE//OC (theo (∗))

Suy ra:  OCA^=EAC^ ( hai góc so le trong)      (1)

Ta có: OA=OC(=R)

Suy ra: ∆OAC cân tại O ⇒OCA^=OAC^  (2)

Từ (1) và (2) suy ra: EAC^=OAC^

Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE.

c) Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên ACB^=90∘

Tam giác ABC vuông tại C có CH⊥AB.

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:

CH2=HA.HB(3)

Xét hai tam giác ACH và ACE, ta có:

+) AEC^=AHC^=90∘

+) CH=CE (tính chất đường phân giác)

+) AC chung

Suy ra:   ∆ACH=∆ACE (cạnh huyền, cạnh góc vuông)

Suy ra:   AH=AE(4)

Xét hai tam giác BCH và BEF, ta có:

+) BHC^=BFC^=90∘

+) CH=CF(=CE)

+) BC chung

Suy ra: ∆BCH=∆BCF (cạnh huyền, cạnh góc vuông)

Suy ra:       BH=BF(5)

Từ (3), (4) và (5) suy ra: CH2=AE.BF

Bài tập bổ sung (trang 163 SBT Toán 9)

(A) Đường vuông góc với AB tại A ;

(B)  Đường vuông góc với AB tại B ;

(C)  Hai đường thẳng song song với AB và cách AB một khoảng 1cm;

(D) Hai đường thẳng song song với AB và cách AB một khoảng 2cm.

Hãy chọn phương án đúng

Phương pháp giải:

Sử dụng kiến thức: Nếu đường thẳng a và đường tròn (O) tiếp xúc với nhau thì d=R, với d là khoảng cách từ  tâm đường tròn đến đường thẳng a.

Lời giải:

Vì AB tiếp xúc với đường tròn (O) nên khoảng cách từ O đến đường thẳng AB bằng bán kính là 2:2=1cm 

Do đó  điểm O nằm trên hai đường thẳng song song với AB và cách AB một khoảng 1cm.

Chọn (C).

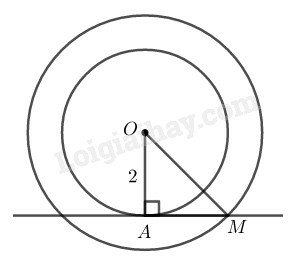
Lời giải:

Vì AM là tiếp tuyến của đường tròn (O) nên AM⊥OA.

Lại có AM=OA=2cm nên ΔOAM là tam giác vuông cân tại A

Theo định lý Pytago ta có: OM2=OA2+AM2=22+22=8

⇒OM=22.

Do điểm O cố định nên điểm M chuyển động trên đường tròn (O;22cm).

Sử dụng kiến thức:

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Sử dụng định lý Ta-lét. 

Lời giải:

Gọi C  là tiếp điểm của EF với đường tròn (O), H là giao điểm của OC và AB. Ta có

OC⊥EF (tính chất tiếp tuyến) và AB//EF (gt) nên OC⊥AB tại H.

Xét đường tròn (O) có OC⊥AB tại H nên H là trung điểm của AB (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy)

Suy ra HB=AB2=12cm 

Xét tam giác OHB vuông tại H, theo định lý Pytago ta có:

OB2=OH2+HB2

 ⇒OH2=OB2−HB2

⇔OH2=152−122=81

 ⇒OH=9cm.

Vì AH//EC nên OHOC=OAOE (định lý Ta-lét)

Vì AB//EF nên ABEF=OHOC (hệ quả định lý Ta-lét)

Suy ra OHOC=ABEF ,

tức là 915=24EF.

⇒EF=24.159=40cm