tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 9: Độ dài đường tròn, cung tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 9: Độ dài đường tròn, cung tròn
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức:
Lời giải:
Gọi phần bán kính tăng thêm của đường tròn bán kính R là a, phần bán kính tăng thêm của đường tròn bán kính r là b. Khi bán kính mỗi đường tròn tăng thêm 1m, ta có:
2π(R+a)=2πR+1⇒2πa=1⇒a=12π(m)
2π(r+b)=2πr+1⇒2πb=1⇒b=12π(m)
Vậy bán kính mỗi đường tròn đều tăng thêm 12π(m).
a) Một lục giác đều có cạnh là 4cm;
b) Một hình vuông có cạnh là 4cm;
c) Một tam giác đều có cạnh là 6cm.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR.
+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
Lời giải:
a)
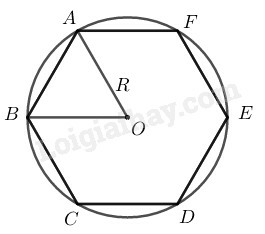
Cạnh lục giác đều nội tiếp trong đường tròn (O;R) bằng bán kính R. Vì cạnh lục giác đều là 4cm ⇒R=4cm.
C=2πR=2.π.4=8π(cm)
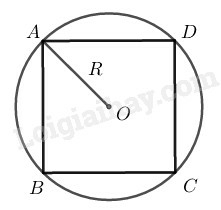
b)
Đường tròn ngoại tiếp hình vuông có đường kính là đường chéo của hình vuông.
Độ dài đường chéo hình vuông có cạnh bằng 4(cm) là AC=AB2+BC2=42(cm) (định lý Pytago)
Bán kính của đường tròn ngoại tiếp hình vuông:
R=422=22
C=2πR=2.π.22=4π2(cm)
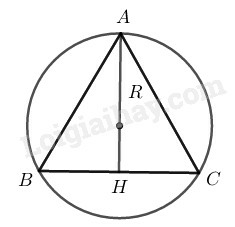
c)
Vì tam giác đều nên giao điểm 3 đường trung trực cũng là giao điểm 3 đường cao, 3 đường trung tuyến nên bán kính của đường tròn ngoại tiếp bằng 23 đường cao của tam giác đều.
Xét tam giác vuông AHB, ta có:
AH=AB.sinB^=6.sin60∘=6.32=33
Bán kính R=23AH=23.33=23(cm)
C=2πR=2π.23=43π(cm).
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR
Lời giải:
Gọi bán kính trái đất là R
Ta có: 2πR=40000(km)
⇒R=400002π≈400006,28≈6369(km)
Ta sử dụng kiến thức:
+) Số đo của nửa đường tròn bằng 180o.
+) Trong đường tròn R, độ dài l của một cung n∘ được tính theo công thức: l=πRn180.
Lời giải:
Ta có cung 180∘ (một nửa đường tròn lớn) có độ dài bằng 20000km.
Độ dài của cung 56∘ là: l=20000.56180≈6222 (km)
Vậy Mát – xcơ – va cách xích đạo khoảng 6222km.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Trong đường tròn R, độ dài l của một cung n∘ được tính theo công thức: l=πRn180.
Lời giải:
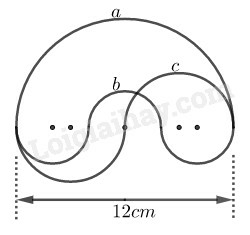
Đường cong a là nửa đường tròn đường kính 12cm
Đường cong a có độ dài l1=12π.12=6π (cm)
Đường cong b gồm 3 nửa đường tròn có đường kính là 4 cm
Đường cong b có độ dài l2=3.12π.4=6π (cm)
Đường cong c gồm hai nửa đường tròn đường kính 6cm.
Đường cong c có độ dài l3=2.12π.6=6π (cm)
Vậy 3 đường cong có độ dài bằng nhau.
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR. Nếu gọi d là đường kính đường tròn (d=2R) thì C=πd.
Lời giải:
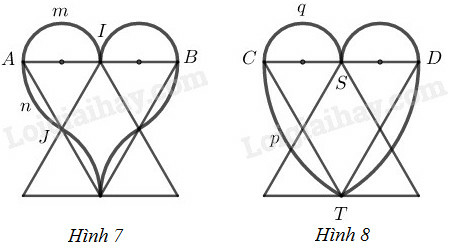
Hình 7 có 2 nửa đường tròn đường kính 4cm và có 4 cung có độ dài là 16 đường tròn bán kính 4cm
AmI⏜ là nửa đường tròn đường kính 4cm, gọi độ dài cung này là l1, có 2 cung như thế.
l1=12π.4=2π (cm)
AnJ⏜ là cung 16 đường tròn bán kính 4cm (trên hình 7 có 4 cung bằng nhau (vì 4 đường tròn đó có cùng bán kính))
Gọi AnJ⏜ có độ dài l2
l2=16.2π.4=43π (cm)
Chu vi hình 7 là: 2.l1+4.l2=2π.2+43π.4=283π (cm)
Hình 8 có hai nửa đường tròn đường kính 4cm và hai cung 16 đường tròn bán kính 8cm
Cung CpS⏜ là nửa đường tròn đường kính 4cm có độ dài l1
l1=12.π.4=2π (cm)
Cung CqT⏜ là 16 đường tròn bán kính 8cm có độ dài l2
l2=16.2π.8=83π (cm)
Chu vi hình 8 bằng: 2.l1+2.l2=2.2π+2.83π=283π (cm)
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR
Lời giải:
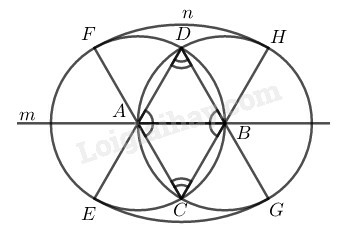
Cách vẽ:
– Vẽ đoạn thẳng AB=3 cm
– Vẽ đường tròn tâm A bán kính 3cm
– Vẽ đường tròn tâm B bán kính 3cm
Đường tròn (A) và đường tròn (B) cắt nhau tại C và D.
– Vẽ cung tròn tâm C bán kính 6cm cắt đường tròn (A) và (B) tại F và H
– Vẽ cũng tròn tâm D bán kính 6cm cắt đường tròn (A) và (B) tại E và G.
Tính chu vi:
Theo cách vẽ, ta có ∆ABD đều, ∆ACD đều.
⇒CAD^=CBD^=1200
FmE⏜ = HG⏜; FnH⏜ = EG⏜
Cung FmE⏜ bằng 13 đường tròn đường kính 3cm nên có độ dài là:
l1=13.2π.3=2π (cm)
Cung FnH⏜ bằng 16 đường tròn bán kính 6cm nên có độ dài là:
l2=16.2π.6=2π (cm)
Chu vi quả trứng bằng:
2l1+2l2=2.2π+2.2π=8π(cm)
Ta sử dụng kiến thức: Trong đường tròn R, độ dài l của một cung n∘ được tính theo công thức: l=πRn180.
Lời giải:
Đổi 36∘45′=147∘4
l=πR.n180 ⇒l=πR.1474180=49240πR
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Trong giác cân, đường cao ứng với cạnh đáy cũng là đường trung tuyến ứng với cạnh đáy.
+) Trong một đường tròn, góc nội tiếp (nhỏ hơn hoặc bằng 90∘) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
+) Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR
Lời giải:
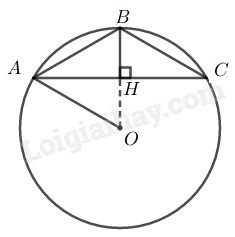
Vẽ đường tròn (O) ngoại tiếp tam giác ABC
∆ABC cân có B^=120∘ nên ∆ABC cân tại B
⇒A^=C^=180∘−120∘2=300
Kẻ BH⊥AC⇒AH=HC=12AC=3 (cm)
Trong tam giác vuông BHA ta có BHA^=900 có:
AB=AHcosA=3cos300=332=23(cm)
Xét đường tròn (O) có: C^=12AOB^ (hệ quả góc nội tiếp)
⇒AOB^=2C^=2.300=600
OA=OB (bán kính)
Suy ra ∆AOB đều nên OA=OB=23(cm)
Độ dài đường tròn ngoại tiếp ∆ABC
C=2πR=2π.23=4π3 (cm)
a) Theo quy tắc đó thì số π được lấy gần đúng là bao nhiêu?
b) Hãy áp dụng quy tắc trên để tính đường kính của một thân cây gần tròn bằng cách dùng dây quấn quanh thân cây.
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR. Nếu gọi d là đường kính đường tròn (d=2R) thì C=πd.
Lời giải:
a) Gọi C là độ dài đường tròn, d là đường kính ⇒π=Cd
Theo quy tắc trên ta tìm được đường kính d như sau:
Lấy C chia làm 8 phần, bỏ đi 3 và phần còn lại chia 2.
Ta có: d=(C8−38C):2
=58C:2=5C16
π=Cd=C5C16=165=3,2
b) Lấy dây quấn quanh thân cây được độ dài đường tròn là C.
Suy ra đường kính thân cây là 516C
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR
Lời giải:
Quãng đường đi của Trái Đất trong một năm là:
2πR=2.3,14.150000000 km
Quãng đường đi của Trái Đất trong 1 ngày là:
2.3,14.150000000365≈2580822
≈2580000km
Bài tập bổ sung (trang 111 SBT Toán 9)
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR
Lời giải:
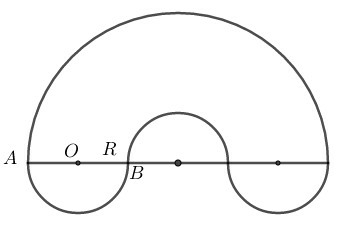
Hình đó gồm một nửa đường tròn bán kính 3R và 3 nửa đường tròn bán kính R
Chu vi của hình đó là:
l=12.2π.3R+3.12.2π.R=6πR
Phương pháp giải:
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Trong đường tròn R, độ dài l của một cung n∘ được tính theo công thức: l=πRn180.
Lời giải:
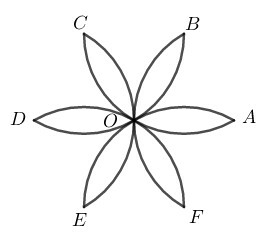
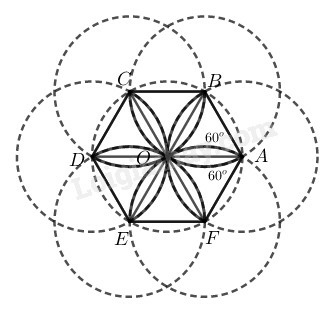
Hình vẽ có 6 cung tròn bằng nhau có bán kính bằng R
BOF⏜ của đường tròn (A;R)
AOC⏜ của đường tròn (B;R)
BOD⏜ của đường tròn (C;R)
COE⏜ của đường tròn (D;R)
DOF⏜ của đường tròn (E;R)
EOA⏜ của đường tròn (F;R)
Vì ABCDEF là lục giác đều nội tiếp đường tròn tâm O (theo cách vẽ hình cánh hoa) nên AB=BC=CD=DE=EF
Từ đó suy ra các tam giác OAB, OBC, OCD, ODE, OEF, OFA bằng nhau (c-c-c)
Nên: AOB^=BOC^=COD^=DOE^=EOF^=FOA^=36006=600
Vì OA=OB và AOB^=600 nên ∆AOB đều, tương tự ta có ∆AOF đều nên BAF^=120∘
⇒sđBOF⏜=120∘
l=πR.120180=2πR3
Chu vi cánh hoa: 2πR3.6=4πR
