tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 2: Tỉ số lượng giác của góc nhọn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 2: Tỉ số lượng giác của góc nhọn
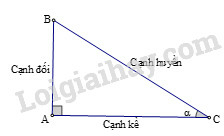
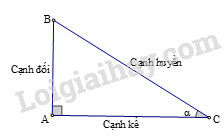
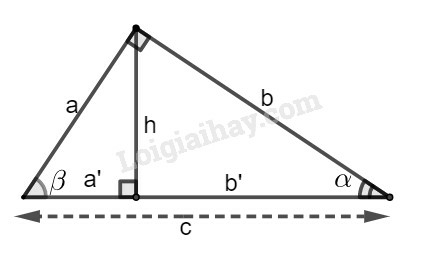
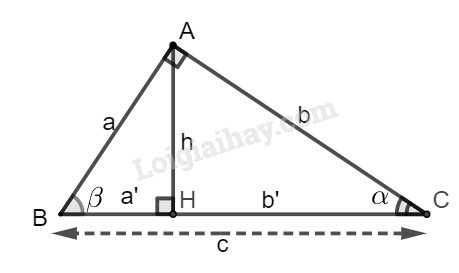
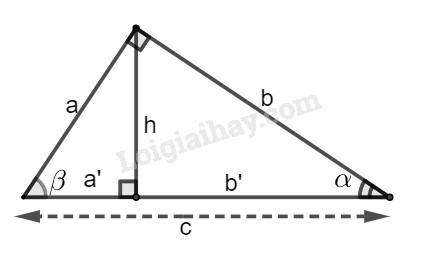
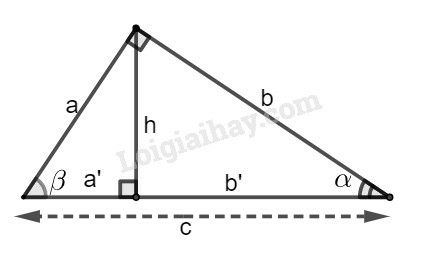
Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:
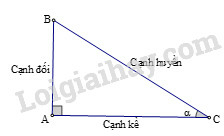
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
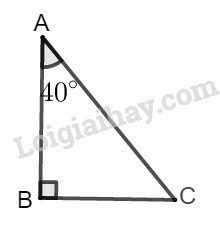
Vẽ tam giác ABC vuông tại B có B^=900,A^=400
Đặt AB=c,AC=b,BC=a.
Ta có:
sin40∘=sinA^=BCAC=ab
cos400=cosA^=ABAC=cb
tg400=tgA^=BCAB=ac
cotg40∘=cotgA^=ABBC=ca
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:
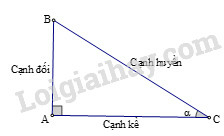
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
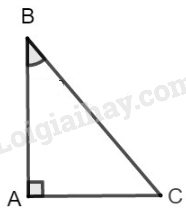
Tam giác ABC có A^=90∘.
Ta có: sinB^=ACBC;sinC^=ABBC
Suy ra: sinB^sinC^=ACBCABBC=ACBC.BCAB=ACAB.
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
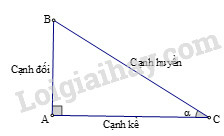
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
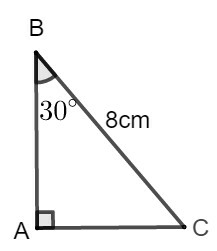
Giả sử tam giác ABC có A^=90∘,B^=30∘,BC=8cm.
Ta có: cosB^=ABBC
Suy ra: AB=BC.cosB^=8.cos30∘=8.0,866≈6,928(cm)
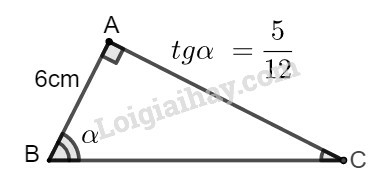
Biết tgα=512. Hãy tính:
a) Cạnh AC;
b) Cạnh BC.
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
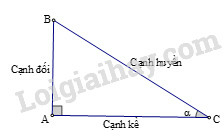
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Định lí Pytago vào tam giác ABC vuông tại A: AB2+AC2=BC2.
Lời giải:
Giả sử tam giác ABC có A^=90∘,B^=α.
a) Ta có: tanα=tanB^=ACAB
Suy ra: AC=AB.tanB^=AB.tanα=6.512=2,5(cm)
b) Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+(2,5)2=42,25
Suy ra: BC=42,25=6,5(cm).
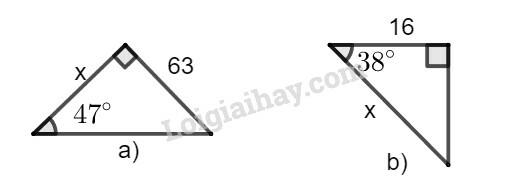
Bài 25 trang 107 SBT Toán 9 tập 1: Tìm giá trị x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình 10, biết rằng:
tg47∘≈1,072;cos38∘≈0,788.
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
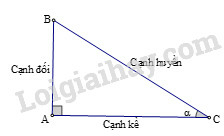
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
a) Hình a
Ta có: tan47∘=63x. Suy ra: x=63tan47∘≈631,072≈58,769
b) Hình b
Ta có: cos38∘=16x. Suy ra: x=16cos38∘≈160,788≈20,305
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
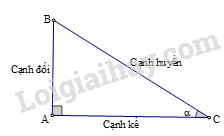
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Định lí Pytago vào tam giác ABC vuông tại A: AB2+AC2=BC2.
Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia và tan góc này bằng cotan góc kia.
Lời giải:
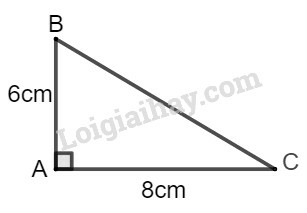
Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+82=100
Suy ra: BC=10(cm)
Ta có:
sinB^=ACBC=810=0,8
cosB^=ABBC=610=0,6
tanB^=ACAB=86=43
cotB^=ABAC=68=34
Vì tam giác ABC vuông tại A nên B^+C^=900
Suy ra:
sinC^=cosB^=0,6
cosC^=sinB^=0,8
tanC^=cotB^=34
cotC^=tanB^=43
Bài 27 trang 107 SBT Toán 9 tập 1: Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB,sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng:
a) AB=13; BH=5.
b) BH=3; CH=4.
Phương pháp giải:
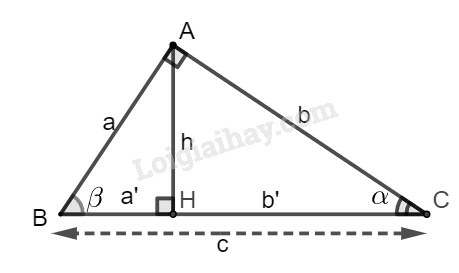
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+) AC2=CH.BC hay b2=ab′
+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
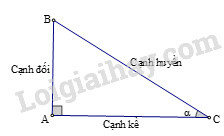
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
a) Xét tam giác vuông ABH, ta có: cosB^=BHAB=513
Tam giác ABC vuông tại A nên: B^+C^=90∘
Suy ra: sinC^=cosB^=513≈0,3864.
Áp dụng định lí Pytago, ta có:
AB2=AH2+BH2⇒AH2=AB2−BH2=132−52=144
Suy ra: AH=12
Ta có: sinB=AHAB=1213≈0,9231
b) Ta có:
BC=BH+HC=3+4=7
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2=BH.BC⇒AB=BH.BC=3.7=21
AC2=CH.BC⇒AC=CH.BC=4.7=28=27
Suy ra: sinB^=ACBC=277≈0,7559
sinC^=ABBC=217≈0,6547
sin75∘,cos53∘,sin47∘20′,tg62∘,cotg82∘45′.
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Với hai góc α,β sao cho α+β=90∘
Ta có: sinα=cosβ; sinβ=cosα;tanα=cotβ; tanβ=cotα.
Lời giải:
Vì 75∘+15∘=90∘ nên sin75∘=cos15∘
Vì 53∘+37∘=90∘ nên cos53∘=sin37∘
Vì 47∘20′+42∘40′=90∘ nên sin47∘20′=cos42∘40′
Vì 62∘+28∘=90∘ nên tg62∘=cot28∘
Vì 82∘45′+7∘15′=90∘ nên cot82∘45′=tg7∘15′
a) sin32∘cos58∘;
b) tg76∘−cotg14∘.
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Với hai góc α,β sao cho α+β=90∘
Ta có: sinα=cosβ; sinβ=cosα;tanα=cotβ; tanβ=cotα.
Lời giải:
a)
Ta có: 32∘+58∘=90∘
Suy ra: sin32∘=cos58∘. Vậy sin32∘cos58∘=cos58∘cos58∘=1.
b)
Ta có: 76∘+14∘=90∘
Suy ra: tg76∘=cotg14∘.
Vậy tg76∘−cotg14∘=cotg14∘−cotg14∘=0.
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:
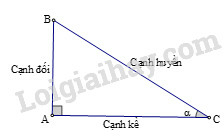
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
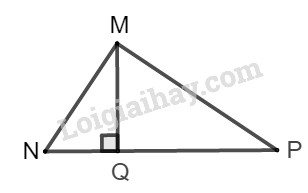
Tam giác MNQ vuông tại Q nên ta có:
cotgN^=NQMQ=3MQ
Tam giác MPQ vuông tại Q nên ta có:
cotgP^=PQMQ=6MQ
Ta có: 6MQ>3MQ nên cotgP^>cotgN^
cotgP^cotgN^=6MQ3MQ = 6MQ.MQ3 = 63=2
Vậy cotgP^=2cotgN^.
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:
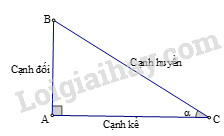
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
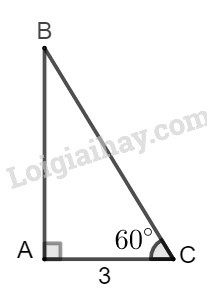
Giả sử tam giác ABC có A^=90∘,C^=60∘,AC=3.
Ta có: cosC^=ACBC
⇒BC=ACcosC^=ACcos60∘=312=6
sin60∘=sinC^=ABBC
Suy ra: AB=BC.sin60∘=6.32=33.
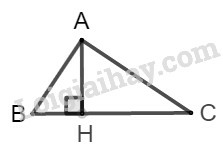
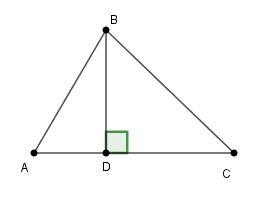
a) Tính diện tích tam giác ABD;
b) Tính AC, dùng các thông tin dưới đây nếu cần:
sinC=35,cosC=45,tgC=34.
Phương pháp giải:
Sử dụng: Công thức tính diện tích tam giác ABC vuông tại A và có đường cao AH là S=12AB.AC=12AH.BC.
Sử dụng tỉ số lượng giác của góc nhọn để tính toán.
Lời giải:
a) Vì tam giác ABD vuông tại D nên ta có:
SΔABD=12.BD.AD=12.6.5=15 (đvdt)
b) Xét tam giác BCD vuông, theo định nghĩa tỉ số lượng giác của góc nhọn ta có: tanC^=BDDC
Theo giả thiết: tanC^=34
Suy ra: BDDC=34⇒DC=43BD=4.63=8
Suy ra: AC=AD+DC=5+8=13.
a sử dụng các kiến thức sau:
sin2α+cos2β=1
tgα=sinαcosα;cotgα=cosαsinα
tgα.cotgα=1.
Lời giải:
Ta có: sin2α+cos2α=1
Suy ra: sin2α=1−cos2α=1−(0,8)2=1−0,64=0,36
Vì sinα>0 nên sinα=0,36=0,6
Suy ra: tanα=sinαcosα=0,60,8=34=0,75
cotα=1tanα=10,75≈1,3333
a) tgα=13
b) cotgα=34.
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
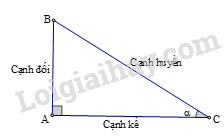
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
a)
Vì tgα=13 nên có thể coi α là góc nhọn của một tam giác vuông có các cạnh góc vuông là 1 và 3.
Suy ra cạnh huyền của tam giác vuông là: 12+32=10≈3,1623
Vậy: sinα=13,1623≈0,3162; cosα=33,1623≈0,9487
b)
Vì cotgα=34 nên có thể coi α là góc nhọn của một tam giác vuông có các cạnh góc vuông là 3 và 4.
Suy ra cạnh huyền của tam giác vuông là: 32+42=25=5
Vậy: sinα=45=0,8; cosα=35=0,6
a) sinα=0,25;
b) cosα=0,75 ;
c) tgα=1;
d) cotgα=2.
Phương pháp giải:
Dựng góc vuông xOy.
– Vận dụng định nghĩa của các tỉ số lượng giác để nhận ra góc α.
– Trên tia Ox dựng đường thẳng OA=m, trên tia Oy dựng đường thẳng OB=n (dựng tùy theo tỉ số lượng giác cosα;sinα dựng đường tròn tâm A bán kính n; với tỉ số lượng giác tgα;cotgα dựng cạnh OB=n).
– Nối đoạn AB.
– Chứng minh cách dựng.
Lời giải:
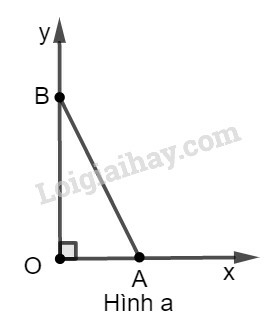
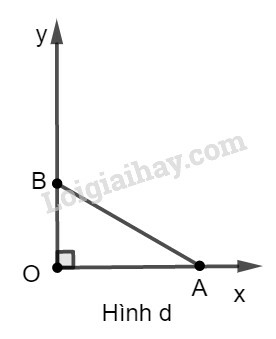
a)
* Cách dựng: hình a
− Dựng góc vuông xOy.
− Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài.
− Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B.
− Nối AB ta được OBA^=α cần dựng.
* Chứng minh: Ta có: sinα=sinOBA^=OAAB=14=0,25
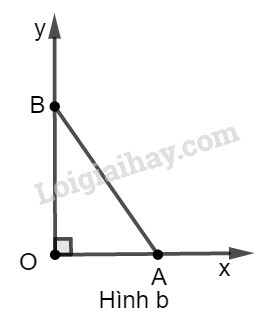
b)
* Cách dựng:hình b:
− Dựng góc vuông xOy.
− Trên tia Ox dựng đoạn OA bằng 3 đơn vị dài.
− Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B.
− Nối AB ta được OAB^=α cần dựng.
* Chứng minh: Ta có: cosOAB^=OAAB=34=0,75
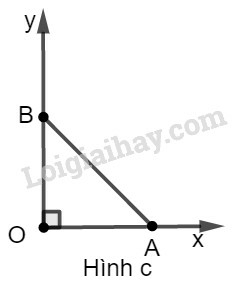
c)
* Cách dựng: hình c
− Dựng góc vuông xOy
− Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài
− Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài
− Nối AB ta được OAB^=α cần dựng
* Chứng minh: Ta có: tgα=tgOAB^=OBOA=11=1
d)
* Cách dựng: hình d
− Dựng góc vuông xOy
− Trên tia Ox dựng đoạn OA bằng 2 đơn vị dài
− Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài
− Nối AB ta được OAB^=α cần dựng
* Chứng minh:
Ta có: cotgα=sinOAB^=OAOB=21=2
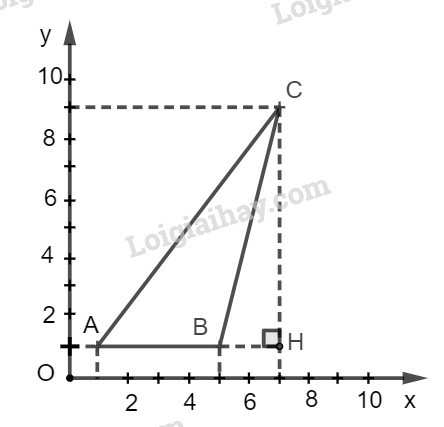
Hãy tính:
a) Giá trị của tgBAC^ (làm tròn đến chữ số thập phân thứ tư);
b) Độ dài của cạnh AC.
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
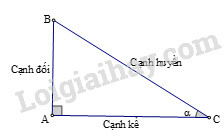
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Định lý Pytago vào tam giác ABC vuông tại A.
AB2+AC2=BC2
Lời giải:
a) Vì tam giác ACH vuông tại H nên ta có:
tgHAC^=CHAH=9−17−1=86≈1,3333
Mà A,B,H thẳng hàng nên suy ra:
tgBAC^=tgHAC^≈1,3333
b) Áp dụng định lí Pytago vào tam giác vuông ACH, ta có:
AC2=CH2+AH2
Suy ra: AC=CH2+AH2=82+62=100=10
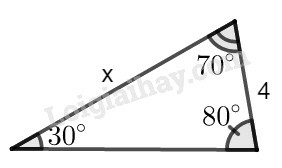
Phương pháp giải:
Sử dụng: sinα=ABBC
Lời giải:
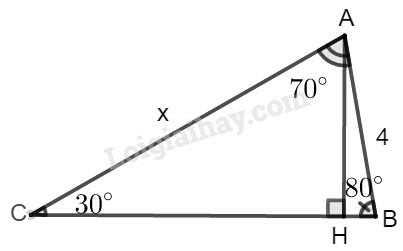
Gọi tên như hình vẽ. Kẻ chiều cao AH
Xét tam giác ACH ta có:
sin300=AHAC⇒AH=x.sin30∘ (1)
Xét tam giác ABH ta có:
sin800=AHAB⇒AH=4.sin80∘ (2)
Từ (1) và (2) : x.sin30∘=4.sin80∘
Phương pháp giải:
Sử dụng: sinα=ABBC
Lời giải:
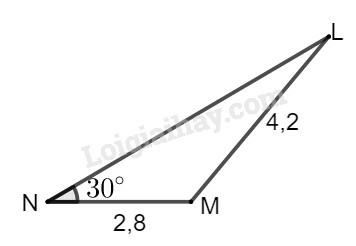
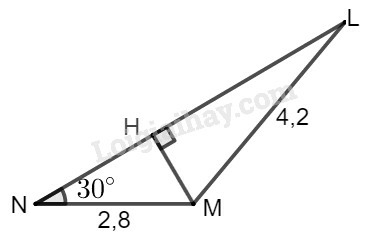
Kẻ MH⊥NL
Xét tam giác vuông NMH ta có: sin30∘=MHMN⇒MH=sin30∘.MN=sin30∘.2,8=1,4
Xét tam giác vuông LMH ta có: sinL=MHML=1,44,2=13≈0,3333.
Bài tập bổ sung (trang 109 SBT Toán 9)
(A) sinα=ab;
(B) sinα=bc;
(C) sinα=b′b;
(D) sinα=hb.
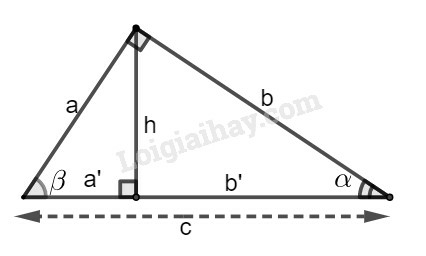
Phương pháp giải:
Sử dụng: sinα=ABBC (hình vẽ)
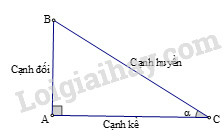
Lời giải:
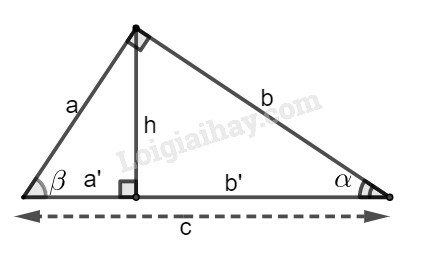
Đặt tên hình như hình dưới đây:
Xét tam giác vuông AHC:
sinα=AHAC=hb.
Vậy chọn đáp án (D).
(A) cosα=ab; (B) cosα=ac;
(C) cosα=bc; (D) cosα=bb′.
Lời giải:
Xét tam giác vuông ABC:
cosα=ACBC=bc.
Vậy chọn đáp án (C).
(A) tgα=ba; (B) tgα=bc ;
(C) tgα=bh; (D) tgα=hb′.
Lời giải:
Xét tam giác vuông AHC:
tgα=AHHC=hb′.
Vậy chọn đáp án (D).
(A) cotgα=ba; (B) cotgα=bc;
(C) cotgα=ac; (D) cotgα=hb.
Lời giải:
Xét tam giác vuông ABC:
cotgα=ACAB=ba.
Vậy chọn đáp án (A).
(A) sinα=sinβ;
(B) sinα=cosβ;
(C) sinα=tgβ;
(D) sinα=cotgβ.
Phương pháp giải:
Với hai góc α,β sao cho α+β=90∘
Ta có: sinα=cosβ; sinβ=cosα;tanα=cotβ; tanβ=cotα.
Lời giải:
Đặt tên hình như hình dưới đây (sử dụng cho các bài 2.5 đến 2.8):
Xét tam giác ABC vuông tại A, ta có:
α+β=90∘
Vậy α,β là hai góc phụ nhau:
sinα=cosβ.
Vậy đáp án đúng là (B).
(A) cosα=cosβ;
(B) cosα=tgβ;
(C) cosα=cotgβ;
(D) cosα=sinβ
Phương pháp giải:
Với hai góc α,β sao cho α+β=90∘
Ta có: sinα=cosβ; sinβ=cosα;tanα=cotβ; tanβ=cotα.
Lời giải:
Xét tam giác vuông ABC ta có:
α+β=90∘
Vậy α,β là hai góc phụ nhau:
cosα=sinβ.
Vậy đáp án đúng là (D).
(A) tgα=tgβ;
(B) tgα=cotgβ;
(C) tgα=sinβ;
(D) tgα=cosβ.
Phương pháp giải:
Với hai góc α,β sao cho α+β=90∘
Ta có: sinα=cosβ; sinβ=cosα;tanα=cotβ; tanβ=cotα.
Lời giải:
Xét tam giác ABC ta có:
α+β=90∘
Vậy α,β là hai góc phụ nhau:
tgα=cotgβ.
Vậy đáp án đúng là (B).
(A) cotgα=tgβ;
(B) cotgα=cotgβ;
(C) cotgα=cosβ;
(D) cotgα=sinβ.
Phương pháp giải:
Với hai góc α,β sao cho α+β=90∘
Ta có: sinα=cosβ; sinβ=cosα;tanα=cotβ; tanβ=cotα.
Lời giải:
Xét tam giác ABC ta có:
α+β=90∘
Vậy α,β là hai góc phụ nhau:
cotgα=tgβ.
Vậy đáp án đúng là (A).
