tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 1: Hàm số bậc hai y=ax^2 (a ≠ 0) chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 1: Hàm số bậc hai y=ax^2 (a ≠ 0)
a) Biểu diễn diện tích toàn phần S (tức là tổng diện tích của sáu mặt) của hình lập phương qua x.
b) Tính các giá trị của S ứng với các giá trị của x cho trong bảng dưới đây rồi điền vào các ô trống.
|
x |
13 | 12 |
1 |
32 |
2 |
3 |
|
S |
|
|
|
|
|
|
c) Nhận xét sự tăng, giảm của khi tăng.
d) Khi S giảm đi 16 lần thì cạnh x tăng hay giảm bao nhiêu lần
e) Tính cạnh của hình lập phương: khi S=272cm2; khi S=5cm2
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích hình vuông bằng bình phương độ dài cạnh.
Lời giải:
a)
Hình lập phương 6 mặt đều là hình vuông, diện tích mỗi mặt bằng x2
Diện tích toàn phần: S=6×2.
b)
|
x |
13 | 12 |
1 |
32 |
2 |
3 |
|
S |
23 |
32 |
6 |
272 |
24 |
54 |
c)
Khi giá trị của x tăng thì giá trị của S tăng.
d)
Khi S giảm đi 16 lần, gọi giá trị của S sau khi giảm là S′ và cạnh hình lập phương sau khi giảm S là x′.
Ta có: S′=6x′2 (1)
S′=S16=6×216=6.×216=6.(x4)2(2)
Từ (1) và (2) suy ra: x′2=(x4)2⇒x′=x4
Vậy cạnh của hình vuông giảm đi 4 lần.
e)
Khi S=272(cm2)
Ta có: 6×2=272⇒x2=272:6=94
Vì x>0 suy ra: x=32(cm)
Khi S=5cm2
⇒6×2=5
⇔x2=56
⇔x=56 (vì x>0)
⇒x=1630(cm).
a) Lập bảng tính các giá trị của y ứng với các giá trị của x lần lượt bằng: −2;−1;−13;0;13;1;2
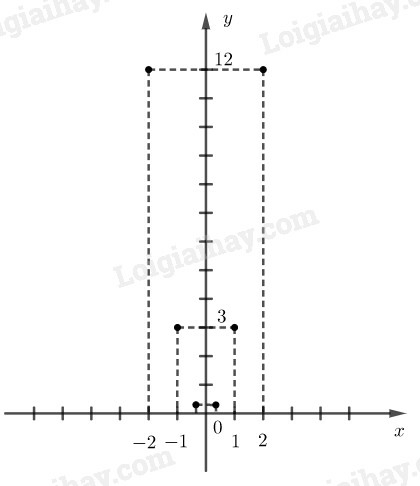
b) Trên mặt phẳng tọa độ xác định các điểm mà hoành độ là giá trị của x còn tung độ là giá trị tương ứng của y đã tìm ở câu a, (chẳng hạn, điểm A(−13;13)
Phương pháp giải:
Ta thay từng giá trị của x vào hàm số ta tính được giá trị y tương ứng.
Lời giải:
a)
|
x |
−2 |
−1 |
−13 |
0 |
13 |
1 |
2 |
| y=3×2 |
12 |
3 |
13 |
0 |
13 |
3 |
12 |
b)
Hình vẽ sau.
a) Lập bảng tính các giá trị của y ứng với các giá trị của x lần lượt bằng: −2;−1;−13;0;13;1;2
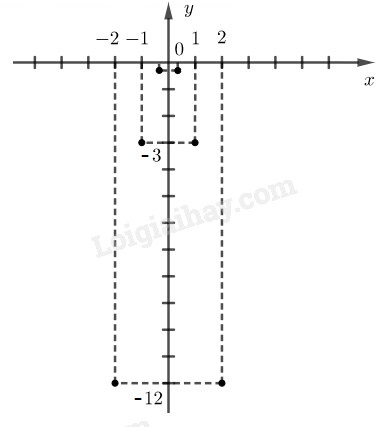
b) Trên mặt phẳng tọa độ xác định các điểm mà hoành độ là giá trị của x còn tung độ là giá trị tương ứng của y đã tìm ở câu a, (chẳng hạn, điểm A(−13;−13))
Phương pháp giải:
Ta thay từng giá trị của x vào hàm số ta tính được giá trị y tương ứng.
Lời giải:
a)
|
x |
−2 |
−1 |
−13 |
0 |
13 |
1 |
2 |
| y=−3×2 |
−12 |
−3 |
−13 |
0 |
−13 |
−3 |
−12 |
b)
Hình vẽ sau.
a) Hãy tính f(1),f(2),f(3) rồi sắp xếp ba giá trị này theo thứ tự từ lớn đến bé.
b) Tính f(−3),f(−2),f(−1) rồi sắp xếp ba số này theo thứ tự từ bé đến lớn.
c) Phát biểu nhận xét của em về sự đồng biến hay nghịch biến của hàm số này khi x>0; khi x<0.
Phương pháp giải:
Thay từng giá trị của x vào rồi ta tính được giá trị y tương ứng.
Lời giải:
a)
f(1)=−1,5.12=−1,5f(2)=−1,5.22=−6f(3)=−1,5.32=−13,5
Ta có: f(1)>f(2)>f(3)
b)
f(−3)=−1,5.(−3)2=−13,5
f(−2)=−1,5.(−2)2=−6f(−1)=−1,5.(−1)2=−1,5
Ta có: f(−3)<f(−2)<f(−1)
c)
Hàm số y=f(x)=−1,5×2 có hệ số a=−1,5<0
Hàm số đồng biến khi x<0, nghịch biến khi x>0
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
0 |
0,24 |
1 |
|
4 |
|
|
a) Biết rằng chỉ có một lần đo không cẩn thận, hãy xác định hệ số a và đố em biết lần đo nào không cẩn thận.
b) Có một thời điểm dừng hòn bi lại nhưng quên không tính thời gian, tuy nhiên đo được đoạn đường đi được của hòn bi (kể từ điểm xuất phát đến điểm dừng) là 6,25m. Đố em biết lần ấy hòn bi đã lăn bao lâu?
c) Hãy điền tiếp vào các ô trống còn lại ở bảng trên.
Phương pháp giải:
Từ công thức hàm số ta rút hệ số a theo y và t, rồi từ đó lập tỉ số giữa y và t mỗi lần đo. Từ đó sẽ tìm được lần đo sai và tìm được hệ số a.
Lời giải:
a)
Ta có: y=at2⇒a=yt2(t≠0)
Ta có: 122=442=14≠0,241 nên a=14. Vậy lần đo đầu tiên sai.
b)
Ta có đoạn đường viên bi lăn y=6,25m. Ta có:
6,25=14t2⇒t=4.6,25=25=5 (giây)
c)
Ta điền thêm các ô trống như sau:
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
0 |
0,24 |
1 |
94 |
4 |
254 |
9 |
a) Hãy điền các số thích hợp vào bảng sau:
|
I (A) |
1 |
2 |
3 |
4 |
|
Q (calo) |
|
|
|
|
b) Hỏi cường độ của dòng điện là bao nhiêu thì nhiệt lượng tỏa ra bằng 60 calo?
Phương pháp giải:
Từ dữ kiện đề bài cho ta rút ra hàm số Q theo I. Rồi ta thay từng giá trị của I ta tìm được giá trị Q tương ứng.
Lời giải:
a)
Q=0,24.RI2t
Dòng điện chạy qua dây dẫn có điện trở 10Ω trong thời gian 1 giây.
Ta có: Q=2,4I2. Ta có kết quả bảng sau:
|
I(A) |
1 |
2 |
3 |
4 |
|
Q (calo) |
2,4 |
9,6 |
21,6 |
38,4 |
b)
Q=60 calo suy ra: 60=0,24.10.I2.1
⇒I2=602,4=25
⇒I=25=5(A)
Bài tập bổ sung (trang 48 SBT Toán 9)
a) Tính thể tích V(x) theo x.
b) Giả sử chiều cao của bể không đổi, hãy tính Nhận xét khi tăng lên lần, lần thì thể tích tương ứng của bể tăng lên mấy lần
Phương pháp giải:
Sử dụng công thức tính thể tích khối hộp: Diện tích đáy nhân với chiều cao.
Chiều cao không thay đổi nên theo câu a ta có: V(x)=2×2.
Lời giải:
a)
Hình hộp chữ nhật đáy hình vuông cạnh x(m) cao 2m.
Thể tích của hộp: V(x)=2×2
b)
V(1)=2.12=2V(2)=2.22=8V(3)=2.32=18
Khi cạnh đáy tăng hai lần thì thể tích tăng 4 lần, cạnh đáy tăng lên 3 lần thì thể tích tăng lên 9 lần.
Phương pháp giải:
Sử dụng kiến thức:
+) Giá trị đối của x là −x.
+) (−a)2=a2.
Lời giải:
Hàm số y=f(x)=ax2(a≠0)
Ta có giá trị đối của x là –x
Nên f(x)=ax2;f(−x)=a(−x)2=ax2
⇒f(x)=f(−x)
Vậy với hai giá trị đối nhau của x thì giá trị tương ứng của hàm số bằng nhau.
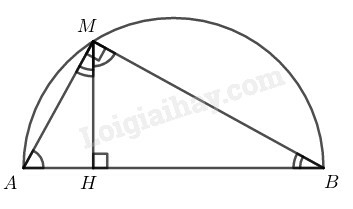
a) Chứng minh rằng hai tam giác AHM và MHB đồng dạng.
b) Chứng minh rằng AH.BH=MH2.
c) Khi M chuyển động thì x thay đổi, do đó tích AH.BH cũng thay đổi theo. Kí hiệu tích AH.BH bởi P(x). Hỏi P(x) có phải là mộhàt m số của biến số x hay không? Viết công thức biểu thị hàm số này.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Nếu hai tam giác đồng dạng ta suy ra được các cạnh tương ứng tỉ lệ.
+) Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x, ta luôn xác địnhđược chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x.
Lời giải:
a) ∆AMB nội tiếp trong đường tròn có AB là đường kính nên AMB^=90∘
Suy ra: MAB^+MBA^=90∘ (1)
∆AMH vuông tại H.
MAH^+HMA^=90∘
hay MAB^+HMA^=90∘ (2)
Từ (1) và (2) suy ra: MBA^=HMA^
hay MBH^=HMA^
Xét ∆AHM và ∆MHB:
AHM^=MHB^=90∘
MBH^=HMA^
Suy ra: ∆AHM đồng dạng ∆MHB(g.g)
b) ∆AHM đồng dạng ∆MHB (theo câu a)
Suy ra MHHA=HBHM⇒HA.HB=HM2
c) Ta có: HA.HB=HM2 (theo câu b)
Suy ra P(x)=x2
Với mỗi giá trị của x ta có một giá trị xác định của P(x).
Vậy P(x)=x2 là một hàm số.
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)