tailieuviet.vn giới thiệu Giải bài tập Toán 9 Bài 4: Liên hệ giữa phép chia và phép khai phương chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Liên hệ giữa phép nhân và phép khai phương 9.
Giải bài tập Toán 9 Bài 4: Liên hệ giữa phép chia và phép khai phương
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 16 SGK Toán 9 Tập 1:Tính và so sánh: 1625 và 1625
Phương pháp giải:
Tính từng biểu thức rồi so sánh.
Lời giải:
Ta có:
+) 1625=(45)2=45
+) 1625=45
⇒1625=1625
Trả lời câu hỏi 2 trang 17 SGK Toán 9 Tập 1:Tính
a) 225256
b) 0,0196
Phương pháp giải:
Sử dụng công thức khai phương 1 thương:
Với a≥0;b>0 ta có ab=ab
Trả lời câu hỏi 3 trang 18 SGK Toán 9 Tập 1:Tính:
Phương pháp giải:
Sử dụng công thức:
Với a≥0;b>0 ta có ab=ab
a) 999111=999111=9=3
b) 52117=52117=49=23
Trả lời câu hỏi 4 trang 18 SGK Toán 9 Tập 1:Rút gọn
a) 2a2b450 b) 2ab2162 với a≥0.
Sử dụng các công thức AB=AB(A≥0;B>0); AB=A.B;A2=|A|; A2=|A|.
Lời giải:
a) Ta có 2a2b450=a2b425=a2b425=a2.b45=a2.(b2)25=|a|b25
b) Ta có 2ab2162=2ab2162=ab281=ab281=a.b29=|b|a9
Bài tập ( trang 18, 19, 20 SGK Toán 9 )
Bài 28 trang 18 SGK Toán 9 Tập 1 :Tính:
a) 289225; b) 21425;
c) 0,259 ; d) 8,11,6.
Phương pháp giải:
+) Sử dụng định lí: Với số a không âm và số b dương, ta có:
ab=ab.
+) Cách đổi hỗn số dương ra phân số:
abc=a.b+cc, với c≠0.
Lời giải:
a) Ta có:
289225=289225=172152=1715.
b) Ta có:
21425=2.25+1425=50+1425
=6425=6425=8252=85.
c) Ta có:
0,259=0,259=0,5232=0,53
=0,5.13=12.13=16.
d) Ta có:
8,11,6=81.0,116.0,1=8116=8116=9242=94.
Bài 29 trang 19 SGK Toán 9 Tập 1: Tính:
a) 218
b) 15735
c) 12500500
d) 6523.35
Phương pháp giải:
Sử dụng các công thức sau:
ab=ab, với a≥0, b>0.
(a.b)m=am.bm, với m∈N.
Lời giải:
a) 218=218=2.12.9=19=(13)2=13.
b) 15735=15735=15.115.49=149=(17)2
=17.
c) 12500500=12500500=500.25500
=25=52=5.
d) 6523.35=6523.35=(2.3)523.35=25.3523.35
=2523=23.2223=22=2
Bài 30 trang 19 SGK Toán 9 Tập 1:Rút gọn các biểu thức sau:
a)yx.x2y4 với x>0, y≠0;
Phương pháp giải:
+) ab=ab, với a≥0, b>0.
+) a2=|a|.
+) |a|=a, nếu a≥0.
|a|=−a, nếu a<0.
+) am.n=am.an, với m, n∈N.
Lời giải:
a) Ta có:
yx.x2y4=yx.x2y4
=yx.x2(y2)2=yx.|x||y2|
Vì x>0 nên |x|=x.
Vì y≠0 nên y2>0⇒|y2|=y2.
⇒yx.|x||y2|=yx.xy2=yx.xy.y=1y.
Vậy yx.x2y4=1y.
b)
2y2.x44y2=2y2.x44y2=2y2.(x2)222.y2
=2y2.(x2)2(2y)2=2y2.|x2||2y|
Vì x2≥0⇒|x2|=x2.
Vì y<0 nên 2y<0⇒|2y|=−2y
⇒2y2.|x2||2y|=2y2.x2−2y=2y2.x2−2y
=x2.y.2y−2y=−x2y.
Vậy 2y2.x44y2=−x2y.
c) Ta có:
5xy.25x2y6=5xy.25x2y6=5xy.52.×2(y3)2
=5xy.(5x)2(y3)2=5xy.|5x||y3|
Vì x<0 nên |5x|=−5x
Vì y>0⇒y3>0⇒|y3|=y3.
⇒5xy.|5x||y3|=5xy.−5xy3=5xy.(−5x)y3
=[5.(−5)].(x.x).yy2.y=−25x2y2
Vậy 5xy.25x2y6=−25x2y2.
d) Ta có:
0,2x3y3.16x4y8=0,2x3y3.16x4y8
=0,2x3y342(x2)2.(y4)2
=0,2x3y3.42(x2)2.(y4)2=0,2x3y3.4|x2|.|y4|.
Vì x≠0, y≠0 nên x2>0 và y4>0
⇒|x2|=x2 và |y4|=y4.
⇒0,2x3y3.4|x2|.|y4|=0,2x3y3.4x2y4
=0,2x3y3.4x2y4
=0,8xy.
Vậy 0,2x3y3.16x4y8=0,8xy.
Tính cụ thể từng kết quả rồi so sánh
Lời giải:
a) Ta có:
+) 25−16=9=32=3.
+) 25−16=52−42=5−4=1.
Vì 3>1⇔25−16>25−16.
Vậy 25−16>25−16
b) Chứng minh rằng: với a>b>0 thì a−b<a−b
Phương pháp giải:
+) Định lí so sánh hai căn bậc hai số học của hai số không âm:
a<b⇔a<b.
+) a2=a, với a≥0.
+) Sử dụng kết quả bài 26 trang 16 SGK toán 9 tập 1: Với hai số dương a,b ta có: a+b<a+b
Lời giải:
Bài ra cho a>b>0 nên a,b và a−b đều xác định và dương.
Ta sẽ so sánh a với a−b+b
Theo kết quả bài 26 trang 16 SGK toán 9 tập 1, với hai số dương a−b và b, ta sẽ có:
a−b+b>a−b+b
Suy ra:
a−b+b>a⇔a−b>a−b
Vậy a−b<a−b với a>b>0.
Cách khác 1:
Với a>b>0 ta có {a>ba−b>0⇒{a−b>0a−b>0
Xét a−b<a−b , bình phương hai vế ta được (a−b)2<(a−b)2⇔(a)2−2.a.b+(b)2<a−b
⇔a−2ab+b<a−b⇔2b−2ab<0
⇔2b(b−a)<0 luôn đúng vì {b>0b−a<0(do0<b<a)
Vậy a−b<a−b với a>b>0.
Cách khác 2:
Bài ra cho a>b>0 nên a,b và a−b đều xác định và dương.
Ta sẽ so sánh a với a−b+b
Ta có a−b+b là số dương và
(a−b+b)2=a−b+2b(a−b)+b=a+2b(a−b)
Rõ ràng 2b(a−b)>0 nên (a−b+b)2>a (1)
Ta có a là số không âm và (a)2=a (2)
Từ (1) và (2) suy ra
(a−b+b)2>(a)2 (3)
Từ (3) theo định lí so sánh các căn bậc hai số học, ta suy ra
(a−b+b)2>(a)2
Hay |a−b+b|>|a|
Hay a−b+b>a
Từ kết quả a<a−b+b, ta có a−b<a−b
Bài 32 trang 19 SGK Toán 9 Tập 1 :Tính
a) 1916.549.0,01
b) 1,44.1,21−1,44.0,4
c) 1652−1242164
d) 1492−7624572−3842
Phương pháp giải:
+ Sử dụng công thức đổi hỗn số ra phân số:
abc=a.c+bc.
+ a2=a , với a≥0.
+ ab=ab, với a≥0, b>0.
+ ab=a.b, với a, b≥0.
Lời giải:
Ta có:
1916.549.0,01=1.16+916.5.9+49.1100
=16+916.45+49.1100
=2516.499.1100
=2516.499.1100
=2516.499.1100
=5242.7232.1102
=54.73.110=5.7.14.3.10=35120=724.
b) Ta có
1,44.1,21−1,44.0,4=1,44(1,21−0,4)
=1,44.0,81
=1,44.0,81
=1,22.0,92
=1,2.0,9=1,08.
c) Ta có:
1652−1242164=(165−124)(165+124)164
=41.28941.4 =2894
=2894 =17222 =172.
d) Ta có:
1492−7624572−3842 =(149−76)(149+76)(457−384)(457+384)
=73.22573.841 =225841
=152292=(1529)2=1529.
Bài 33 trang 19 SGK Toán 9 Tập 1 :Giải phương trình
a) 2.x−50=0
b) 3.x+3=12+27
c) 3.x2−12=0
d)x25−20=0
Phương pháp giải:
Sử dụng các công thức
+ AB=A.B(A;B≥0)
+ AB=AB (với A≥0;B>0)
+ A2=|A|={AkhiA≥0−AkhiA<0
Lời giải:
a) 2.x−50=0
⇔2x=50
⇔x=502
⇔x=502
⇔x=25
⇔x=52
⇔x=5.
Vậy x=5.
b)
3.x+3=12+27
⇔3.x=12+27−3
⇔3.x=4.3+9.3−3
⇔3.x=4.3+9.3−3
⇔3.x=22.3+32.3−3
⇔3.x=23+33−3
⇔3.x=(2+3−1).3
⇔3.x=43
⇔x=4.
Vậy x=4.
c)
3×2−12=0
⇔3×2=12
⇔3×2=4.3
⇔3×2=4.3
⇔x2=4
⇔x2=22
⇔x2=2
⇔x2=2
⇔|x|=2
⇔x=±2.
Vậy x=±2.
d)
x25−20=0
⇔x25=20
⇔x2=20.5
⇔x2=20.5
⇔x2=100
⇔x2=102
⇔x2=10
⇔x2=10
⇔|x|=10
⇔x=±10.
Vậy x=±10.
Bài 34 trang 19 SGK Toán 9 Tập 1:Rút gọn các biểu thức sau:
a) ab2.3a2b4 với a<0, b≠0
b) 27(a−3)248 với a>3
c) 9+12a+4a2b2 với a≥−1,5 và b<0.
d) (a−b).ab(a−b)2 với a<b<0
Phương pháp giải:
Sử dụng các công thức:
+ ab=ab với a≥0;b>0
+ A2=|A|={AkhiA≥0−AkhiA<0
Lời giải:
a) Ta có:
ab2.3a2b4=ab2.3a2b4 =ab2.3a2.b4
=ab2.3a2.(b2)2 =ab2.3|a|.|b2|
=ab2.3−ab2=−3.
(Vì a<0 nên |a|=−a và b≠0 nên b2>0⇒|b2|=b2).
b) Ta có:
27(a−3)248=2748.(a−3)2 =2748.(a−3)2
=9.316.3.(a−3)2 =916.(a−3)2
=3242.(a−3)2 =3242.(a−3)2
=34|a−3|=34(a−3).
( Vì a>3 nên a−3>0⇒|a−3|=a−3)
c) Ta có:
9+12a+4a2b2=32+2.3.2a+22.a2b2
=32+2.3.2a+(2a)2b2=(3+2a)2b2
=(3+2a)2b2=|3+2a||b|
Vì a≥−1,5⇒a+1,5>0
⇔2(a+1,5)>0
⇔2a+3>0
⇔3+2a>0
⇒|3+2a|=3+2a
Vì b<0⇒|b|=−b
Do đó: |3+2a||b|=3+2a−b=−3+2ab.
Vậy 9+12a+4a2b2=−3+2ab.
d) Ta có:
(a−b).ab(a−b)2=(a−b).ab(a−b)2
=(a−b).ab|a−b|
=(a−b).ab−(a−b)=−ab.
(Vì a<b<0 nên a−b<0⇒|a−b|=−(a−b) và ab>0).
Bài 35 trang 20 SGK Toán 9 Tập 1 :Tìm x, biết:
a) (x−3)2=9
b) 4×2+4x+1=6
Phương pháp giải:
Sử dụng hằng đẳng thức A2=|A| đưa phương trình về dạng |A|=m(m≥0)⇔[A=mA=−m
Lời giải:
Ta có:
(x−3)2=9⇔|x−3|=9
⇔[x−3=9x−3=−9⇔[x=9+3x=−9+3
⇔[x=12x=−6
Vậy phương trình đã cho có hai nghiệm: x=12 và x=−6.
b) Ta có:
4×2+4x+1=6⇔22×2+4x+1=6
⇔(2x)2+2.2x+12=6
⇔(2x+1)2=6
⇔|2x+1|=6
⇔[2x+1=62x+1=−6⇔[2x=6−12x=−6−1⇔[2x=52x=−7⇔[x=52x=−72
Vậy phương trình có 2 nghiệm x=52 và x=−72.
Bài 36 trang 20 SGK Toán 9 Tập 1: Mỗi khẳng định sau đúng hay sai ? Vì sao ?
a) 0,01=0,0001;
b) −0,5=−0,25;
c) 39<7 và 39>6;
d) (4−13).2x<3(4−13)⇔2x<3.
+ A xác định (hay có nghĩa) khi A≥0.
+) Sử dụng định lí so sánh hai căn bậc hai:
a<b⇔a<b, với a, b≥0.
+ a.c>b.c⇔a>b , với c>0.
Lời giải:
a) Đúng. Vì 0,0001=0,012=0,01
Vì VP=0,0001=0,012=0,01=VT.
b) Sai.
Vì vế phải không có nghĩa do số âm không có căn bậc hai.
c) Đúng.0,0001=0,012=0,01
Vì: 36<39<49 ⇔36<39<49
⇔62<39<72
⇔6<39<7
Hay 39>6 và 39<7.
d) Đúng.
Xét bất phương trình đề cho:
(4−13).2x<3.(4−13) (1)
Ta có:
16>13⇔16>13
⇔42>13
⇔4>13
⇔4−13>0
Chia cả hai vế của bất đẳng thức (1) cho số dương (4−13), ta được:
(4−13).2x(4−13)<3.(4−13)(4−13)
⇔2x<3.
Vậy phép biến đổi tương đương trong câu d là đúng.
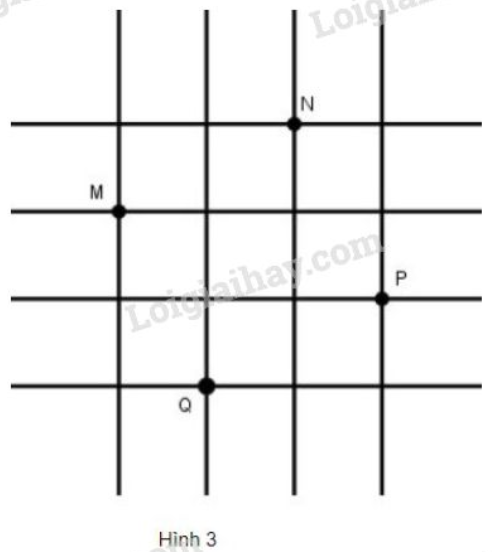
Bài 37 trang 20 SGK Toán 9 Tập 1 :Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm, cho bốn điểm M, N, P, Q (h.3).
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQ.
+ Sử dụng định lí Py-ta-go trong tam giác vuông.
+ Công thức tính diện tích hình vuông cạnh a là: S=a2.
+ Dấu hiệu nhận biết hình vuông: hình thoi có hai đường chéo bằng nhau (hay tứ giác có bốn cạnh bằng nhau và có hai đường chéo bằng nhau) thì là hình vuông.
Lời giải:
Nối các điểm ta có tứ giác MNPQ
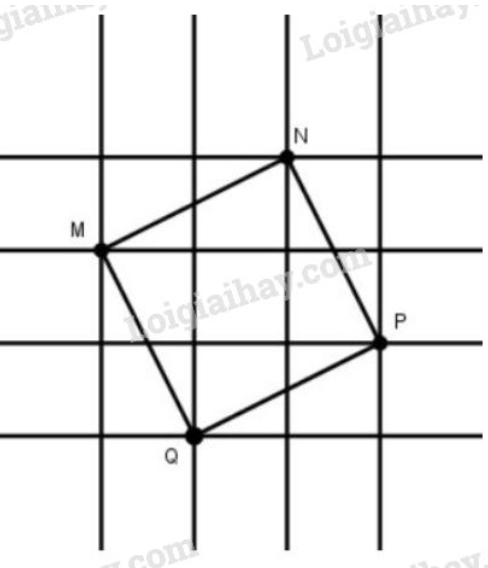
Tứ giác MNPQ có:
– Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 2cm, chiều rộng 1cm. Do đó theo định lí Py-ta-go, ta có:
MN=NP=PQ=QM=22+12=5(cm).
Hay MNPQ là hình thoi.
– Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 3cm, chiều rộng 1cm nên theo định lý Py-ta-go ta có độ dài đường chéo là:
MP=NQ=32+12=10(cm).
Như vậy hình thoi MNPQ có hai đường chéo bằng nhau nên MNPQ là hình vuông.
Vậy diện tích hình vuông MNPQ bằng MN2=(5)2=5(cm2).
Lý thuyết Bài 4: Liên hệ giữa phép chia và phép khai phương
1. Định lí
Với số a không âm và số b dương ta có: ab=ab.
2. Quy tắc khai phương một thương
Muốn khai phương một thương ab, trong đó a không âm, b dương, ta có thể khai phương lần lượt a và b rồi lấy kết quả thứ nhất chia cho kết quả thứ 2.
3. Quy tắc chia các căn bậc hai
Muốn chia các căn bậc hai của số a không âm cho căn bậc hai của số b dương ta có thể chia a cho cho b rồi khai phương kết quả đó.
Chú ý: Một cách tổng quát, với biểu thức A không âm và biểu thức B dương ta có AB=AB
4. Các dạng toán cơ bản
Dạng 1: Tính giá trị biểu thức
Sử dụng: Với biểu thức A không âm và biểu thức B dương ta có AB=AB
Ví dụ: 2549=2549=57
Dạng 2: Rút gọn biểu thức
Sử dụng: Với biểu thức A không âm và biểu thức B dương ta có AB=AB
Ví dụ: Rút gọn 27y33y với y>0
Ta có: 27y33y=27y33y=9y2=(3y)2=|3y|=3y
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)