tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 3: Đồ thị của hàm số y=ax+b (a≠0) chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 3: Đồ thị của hàm số y=ax+b (a≠0)
a) Vẽ đồ thị của các hàm số sau trên cũng một mặt phẳng tọa độ:
y=x+3; (1)
y=2x+3; (2)
b) Gọi giao điểm của đường thẳng y=x+3 với các trục Oy, Ox theo thứ tự là A, B và giao điểm của đường thẳng y=2x+3 với các trục Oy, Ox theo thứ tự là A, C. Tính các góc của tam giác ABC (dùng máy tính bỏ túi CASIO fx-220 hoặc CASIO fx-500A).
Phương pháp giải:
Cách vẽ đồ thị hàm số y=ax+b (a≠0)
+ Nếu b=0 ta có hàm số y=ax . Đồ thị của y=ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A(1;a);
+ Nếu b≠0 thì đồ thị y=ax+b là đường thẳng đi qua các điểm A(0;b); B(−ba;0).
Lời giải:
a)
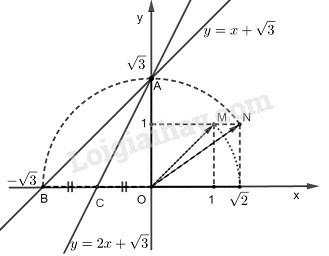
*) Vẽ đồ thị của hàm số y=x+3
Cho x = 0 thì y=3. Ta có: A(0;3)
Cho y = 0 thì x+3=0⇒x=−3. Ta có: B(−3;0)
*) Cách tìm điểm có tung độ bằng 3 trên trục Oy:
– Dựng điểm M(1;1). Ta có: OM=12+12=2
– Dựng cung tròn tâm O bán kính OM cắt trục Ox tại điểm có hoành độ bằng 2 .
– Dựng điểm N(1;2). Ta có: ON=12+(2)2=3
– Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ 3 cắt tia đối của Ox tại B có hoành độ −3 .
Đồ thị của hàm số y=x+3 là đường thẳng AB.
*) Vẽ đồ thị của hàm số y=2x+3
Cho x = 0 thì y=3. Ta có: A(0;3)
Cho y = 0 thì 2x+3=0⇒x=−32. Ta có: C(−32;0)
Đồ thị của hàm số y=2x+3 là đường thẳng AC
b)
Xét tam giác ABO vuông tại O, có: tgABO^=OAOB=33=1⇒ABO^=450 hay ABC^=450
Xét tam giác ACO vuông tại O, có: tgACO^=OAOC=332=2⇒ACO^=63026′
Ta có: ACO^+ACB^=1800 (hai góc kề bù)
Suy ra : ACB^=1800−ACO^=1800−63026′=116034′
Lại có: ACB^+ABC^+BAC^=1800 (tổng ba góc trong tam giác ABC)
Suy ra:
BAC^=1800−(ACB^+ABC^)=1800−(450+116034′)=18026′
a) Với các giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Xác định giá trị của m để đồ thị hàm số đi qua điểm A(1;2).
c) Xác định giá trị của m để đồ thị hàm số đi qua điểm B(1;−2).
d) Vẽ đồ thị của hai hàm số ứng với giá trị của m tìm được ở các câu b) , c).
Phương pháp giải:
Hàm số bậc nhất là hàm số được cho bởi công thức y=ax+b, trong đó a,b là các số cho trước và a≠0.
Hàm số bậc nhất y=ax+b xác định với mọi giá trị của x thuộc R và có tính chất sau:
a) Đồng biến trên R, khi a>0.
b) Nghịch biến trên R, khi a<0.
Lời giải:
a)
Điều kiện : m−3≠0⇔m≠3.
*) Hàm số đồng biến khi hệ số a=m−3>0⇔m>3
Vậy với m>3 thì hàm số y=(m−3)x đồng biến.
*) Hàm số nghịch biến khi hệ số a=m−3<0⇔m<3
Vậy với m<3 thì hàm số y=(m−3)x nghịch biến.
b)
Đồ thị của hàm số y=(m−3)x đi qua điểm A(1;2) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có: 2=(m−3)1⇔2=m−3⇔m=5
Vậy với m=5 thì đồ thị hàm số y=(m−3)x đi qua điểm A(1;2)
c)
Đồ thị của hàm số y=(m−3)x đi qua điểm B(1;-2) nên tọa độ điểm B nghiệm đúng phương trình hàm số.
Ta có : −2=(m−3)1⇔−2=m−3⇔m=1
Vậy với m=1 thì đồ thị hàm số y=(m−3)x đi qua điểm B(1;-2).
d)
Khi m=5 thì ta có hàm số: y=2x
Khi m=1 thì ta có hàm số: y=−2x
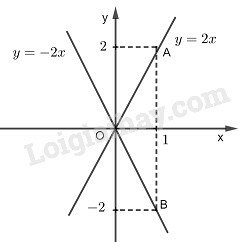
*) Vẽ đồ thị của hàm số y=2x
Cho x=0 thì y=0. Ta có: O(0;0)
Cho x=1 thì y=2. Ta có: A(1;2)
Đường thẳng OA là đồ thị hàm số y=2x.
*) Vẽ đồ thị của hàm số y=−2x.
Cho x=0 thì y=0. Ta có : O(0;0)
Cho x=1 thì y=−2 . Ta có : B(1;-2)
Đường thẳng OB là đồ thị của hàm số y=−2x.
a) Xác định giá trị của a để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2.
b) Xác định giá trị của a để đồ thị hàm số cắt trục tung tại điểm có hoành độ bằng −3.
c) Vẽ đồ thị của hai hàm số ứng với giá trị của a tìm được ở các câu a) , b) trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
Phương pháp giải:
Điểm M(x0;y0) thuộc đồ thị y=ax+b khi y0=ax0+b
Lời giải:
a)
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng y=2, suy ra điểm đó có hoành độ x=0.
Thay x=0, y=2 vào hàm số y=(a−1)x+a(a≠1) ta được:
2=(a−1).0+a⇒a=2 (thỏa mãn)
Vậy a=2.
Cách khác:
Hàm số y=(a−1)x+a(a≠1) là hàm số bậc nhất có đồ thị hàm số cắt trục tung tại điểm có tung độ bằng y=2 nên a=2.
b)
Hàm số y=(a−1)x+a(a≠1) là hàm số bậc nhất có đồ thị hàm số cắt trục hoành tại điểm có hoành độ x=−3 nên tung độ giao điểm này bằng 0.
Ta có:
0=(a−1)(−3)+a⇔−3a+3+a=0⇔−2a=−3⇔a=1,5
c)
Khi a=2 thì ta có hàm số: y=x+2
Khi a=1,5 thì ta có hàm số: y=0,5x+1,5
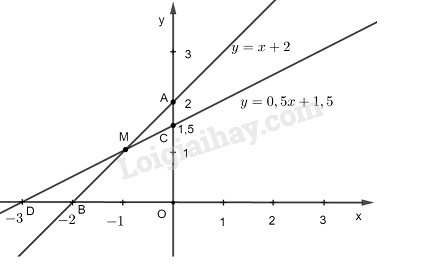
* Vẽ đồ thị của hàm số y=x+2
Cho x=0 thì y=2. Ta có: A(0;2)
Cho y=0 thì x=−2. Ta có: B(−2;0)
Đường thẳng AB là đồ thị hàm số y=x+2.
* Vẽ đồ thị của hàm số y=0,5x+1,5
Cho x=0 thì y=1,5. Ta có: C(0;1,5)
Cho y=0 thì x=−3. Ta có : D(−3;0)
Đường thẳng CD là đồ thị hàm số y=0,5x+1,5
* Tọa độ giao điểm của hai đường thẳng .
Gọi M(x1;y1) là giao điểm của hai đường thẳng y=x+2 và y=0,5x+1,5.
Ta có:
M(x1;y1) thuộc đường thẳng y=x+2 nên y1=x1+2
M(x1;y1) thuộc đường thẳng y=0,5x+1,5 nên y1=0,5×1+1,5
Suy ra:
x1+2=0,5×1+1,5⇔0,5×1=−0,5⇔x1=−1
x1=−1⇒y1=−1+2=1
Vậy tọa độ giao điểm của hai đường thẳng là M(−1;1).
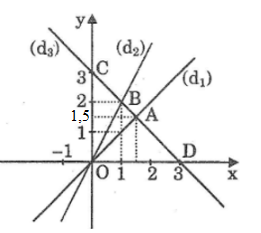
a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau:
y=x (d1) ;
y=2x (d2);
y=−x+3 (d3).
b) Đường thẳng (d3) cắt các đường thẳng (d1); (d2) theo thứ tự tại A,B.
Tìm tọa độ của các điểm và tính diện tích tam giác
Phương pháp giải:
Cách vẽ đồ thị hàm số y=ax+b (a≠0)
+ Nếu b=0 ta có hàm số y=ax . Đồ thị của y=ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A(1;a);
+ Nếu b≠0 thì đồ thị y=ax+b là đường thẳng đi qua các điểm A(0;b); B(−ba;0).
Lời giải:
a)
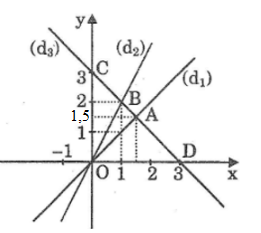
* Vẽ đồ thị của hàm số y=x
Cho x=0 thì y=0
Cho x=1 thì y=1
Đồ thị hàm số y=x là đường thẳng đi qua gốc tọa độ O(0;0) và điểm (1;1)
* Vẽ đồ thị của hàm số y=2x
Cho x=0 thì y=0
Cho x=1 thì y=2
Đồ thị hàm số y=2x là đường thẳng đi qua gốc tọa độ O(0;0) và điểm (1;2)
* Vẽ đồ thị của hàm số y=−x+3
Cho x=0 thì y=3. Ta có điểm (0;3)
Cho y=0 thì x=3. Ta có điểm (3;0)
Đồ thị hàm số y=−x+3 là đường thẳng đi qua hai điểm (0;3) và điểm (3;0)
b)
* Gọi A(x1;y1),B(x2;y2) lần lượt là tọa độ giao điểm của đường thẳng (d3) với hai đường thẳng (d1); (d2).
Ta có: A(x1;y1) thuộc đường thẳng (d1):y=x nên y1=x1
A(x1;y1) thuộc đường thẳng (d3):y=−x+3 nên y1=−x1+3
Suy ra:
x1=−x1+3⇔2×1=3⇔x1=1,5
x1=1,5⇒y1=1,5
Vậy tọa độ giao điểm của hai đường thẳng (d1) và (d3) là A(1,5;1,5).
Ta có:
B(x2;y2) thuộc đường thẳng (d2):y=2x nên y2=2×2
B(x2;y2) thuộc đường thẳng (d3):y=−x+3 nên y2=−x2+3
Suy ra :
2×2=−x2+3⇔3×2=3⇔x2=1
x2=1⇒y2=2
Vậy tọa độ giao điểm của hai đường thẳng (d2) và (d3) là B(1;2).
Tính diện tích tam giác OAB.
SOBD=12.2.3=3(cm2)SOAD=12.1,5.3=2,25(cm2)⇒SOAB=SOBD−SOAD=3−2,25=0,75(cm2)
Bài tập bổ sung (trang 64,65 SBT Toán 9)
a) Khi m=3, đồ thị của hàm số (1) đi qua điểm:
(A) (2; 7); (B) (2,5; 8);
(C) (2; 8); (D) (-2; 3)
b) Khi m=2, đồ thị của hàm số (1) cắt trục hoành tại điểm:
(A) (1; 0); (B) (2; 0);
(C) (-1; 0); (D) (-10; 0)
Phương pháp giải:
Điểm M(x0;y0) thuộc đồ thị y=ax+b khi y0=ax0+b
Lời giải:
a)
Với m=3 thì hàm số có dạng y=1,5x+5
Ta có với
x=2 thì y=1,5.2+5=8 nên đồ thị đi qua điểm (2;8). Do đó A sai, C đúng.
x=2,5 thì y=1,5.2,5+5=8,75≠8 nên B sai
x=−2 thì y=1,5.(−2)+5=2≠3 nên D sai
Vậy đáp án (C).
b)
Với m=2 thì hàm số có dạng y=0,5x+5
x=−10 thì y=1,5.(−10)+5=0 nên đồ thị của hàm số (1) cắt trục hoành tại điểm (-10;0).
Vậy đáp án (D)
y=0,5x−3 (d1); y=−1,5x+5 (d2)
Đường thẳng (d1) và đường thẳng (d2) cắt nhau tại điểm :
(A) (2;−2); (B) (4;−1);
(C) (−2;−4); (D) (8;1).
Phương pháp giải:
Xét đường thẳng (d1): y=a1x+b1 và đường thẳng (d2): y=a2x+b2
Để tìm giao điểm giữa hai đường thẳng ta xét phương trình hoành độ giao điểm:
a1x+b1=a2x+b2.
Tìm x0 là nghiệm của phương trình trên và thay vào một trong hai phương trình đường thẳng để tìm y0. Vậy (x0;y0) là giao điểm cần tìm.
Lời giải:
Xét phương trình hoành độ giao điểm của (d1) và (d2):
0,5x−3=−1,5x+5⇔2x=8⇔x=4
Thay x=4 vào hàm số y=0,5x−3, ta có: y=0,5.4−3=−1.
Vậy giao điểm của hai đường thẳng là: B(4;−1). Đáp án (B).
y=35x−52 (d2); y=kx+3,5 (d3)
Hãy tìm giá trị của k để sao cho ba đường thẳng đồng quy tại một điểm.
Phương pháp giải:
Xét đường thẳng (d1): y=a1x+b1 và đường thẳng (d2): y=a2x+b2
Để tìm giao điểm giữa hai đường thẳng, ta xét phương trình hoành độ giao điểm:
a1x+b1=a2x+b2.
Tìm x0 là nghiệm của phương trình trên và thay vào một trong hai phương trình đường thẳng để tìm y0. Vậy (x0;y0) là giao điểm cần tìm.
Thay tọa độ giao điểm vừa tìm được vào phương trình đường thẳng (d3) để tìm k.
Lời giải:
* Trước hết tìm giao điểm của hai đường thẳng (d1) và (d2).
+) Xét phương trình hoành độ giao điểm của (d1) và (d2):
25x+12=35x−52⇔25x−35x=−52−12⇔−15x=−3⇔x=15
+) Tìm tung độ giao điểm: Thay x=15 vào hàm số y=25x+12, ta có:
y=25.15+12=6,5
+) Thay x=15 và y=6,5 vào phương trình (d3):
6,5=k.15+3,5⇔15k=3⇔k=0,2
Vậy với k=0,2 thì ba đường thẳng đồng quy tại điểm (15;6,5).
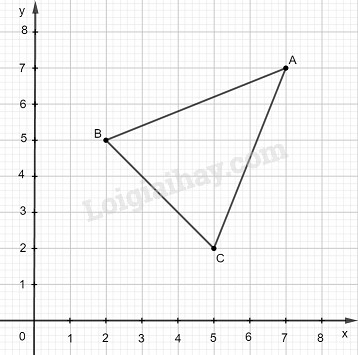
a) Hãy viết phương trình các đường thẳng AB, BC, CA.
b) Coi độ dài mỗi đơn vị trên các trục Ox, Oy là 1cm, hãy tính chu vi, diện tích của tam giác ABC (lấy chính xác đến hai chữ số thập phân).
Phương pháp giải:
Để viết phương trình đường thẳng đi qua hai điểm cho trước ta thực hiện các bước sau:
Bước 1: Gọi phương trình đường thẳng là y=ax+b.
Bước 2: Thay tọa độ các điểm thuộc đường thẳng, ta có các phương trình hai ẩn của a và b.
Bước 3: Từ các phương trình tìm a và b
Bước 4: Kết luận phương trình đường thẳng với a và b đã tìm được.
Lời giải:
a)
+ Gọi phương trình đường thẳng AB là y=ax+b.
Tọa độ của các điểm A, B thỏa mãn phương trình y=ax+b nên ta có:
{7=a.7+b5=a.2+b⇔{b=7−7ab=5−2a
Suy ra: 7−7a=5−2a⇔5a=2⇔a=25
⇒b=5−2a=5−2.25=215
Vậy phương trình đường thẳng AB là y=25x+215
+ Gọi phương trình đường thẳng BC là y=a′x+b′.
Tọa độ của các điểm B, C thỏa mãn phương trình y=a′x+b′ nên ta có:
{5=a′.2+b′2=a′.5+b′⇒{b′=5−2a′b′=2−5a′
Suy ra: 5−2a′=2−5a′⇔3a′=−3⇔a′=−1
⇒b=5−2a′=5−2.(−1)=7
Vậy phương trình đường thẳng BC là y=−x+7.
+ Gọi phương trình đường thẳng AC là y=a″x+b″.
Tọa độ của các điểm A, C thỏa mãn phương trình y=a″x+b″ nên ta có:
{7=a″.7+b″2=a″.5+b″⇒{b″=7−7a″b″=2−5a″
Suy ra: 7−7a″=2−5a″⇔2a″=5⇔a″=52
⇒b″=2−5a″=2−5.52=−212
Vậy phương trình đường thẳng AC là y=52x−212
b)
Áp dụng định lí Pytago vào các tam giác vuông lần lượt có các cạnh huyền AB, AC, BC ta tính được độ dài các cạnh như sau:
AB=52+22=29≈5,39cm
AC=52+22=29≈5,39cm
BC=32+32=18≈4,24cm
Do đó chu vi của tam giác ABC là AB+AC+BC≈5,39+5,39+4,24=15,02cm.
Diện tích tam giác ABC được tính bằng hiệu diện tích hình vuông cạnh 5cm trừ đi ba diện tích của các tam giác xung quanh.
SABC=52−12.5.2−12.5.2−12.3.3=10,5(cm2)
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)