SBT Toán 9 Phần hình học: Ôn tập cuối năm | Giải SBT Toán lớp 9 

tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Phần hình học: Ôn tập cuối năm chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Phần hình học: Ôn tập cuối năm

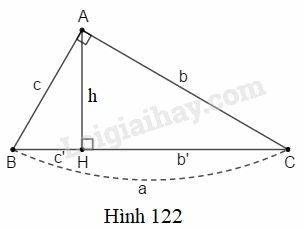
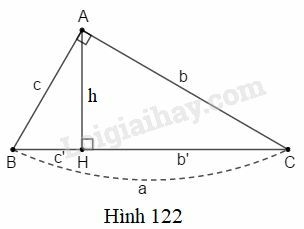
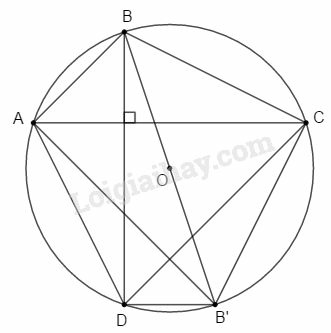
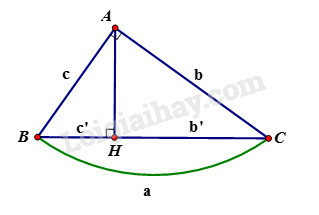
Bài 1 trang 195 SBT Toán 9 tập 2: (Xem hình 122). Tính:

a) h,b và c, biết b′=25,c′=16;

b)  a,c và c′, biết b=12,b′=6;

c) a,b và b′, biết c=8,c′=4;

d) h,b,c′,b′, biết c=6,a=9.

Phương pháp giải:

Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:

+) AB2=BH.BC hay c2=a.c′ 

+) AC2=CH.BC hay b2=ab′

+) AH2=HB.HC hay h2=c′.b′

+) 1AH2=1AB2+1AC2 hay 1h2=1b2+1c2

+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)

Lời giải:

a) a=b′+c′=25+16=41

Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác ABC vuông tại A, ta có:

h2=b′c′=25.16=400⇒h=400=20b2=a.b′=41.25=1025⇒b=1025=541c2=a.c′=41.16=656⇒c=656=441

b) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác ABC vuông tại A, ta có:

b2=a.b′⇒a=b2b′=1226=24c′=a−b′=24−6=18c2=a.c′=24.18=432c=432=123

c) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác ABC vuông tại A, ta có:

c2=a.c′⇒a=c2c′=824=16b′=a−c′=16−4=12b2=a.b′=16.12=192⇒b=192=83

d) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác ABC vuông tại A, ta có:

c2=a.c′⇒c′=c2a=629=4b′=a−c′=9−4=5h2=b′.c′=5.4=20⇒h=20=25b2=a.b′=9.5=45⇒b=45=35

Bài 2 trang 195 SBT Toán 9 tập 2: (Xem hình 122). Chứng minh rằng:

a)h=bca;b)b2b′=c2c′.

Phương pháp giải:

– Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:

+) AB2=BH.BC hay c2=a.c′ 

+) AC2=CH.BC hay b2=ab′

– Diện tích tam giác bằng 12 tích của chiều cao hạ từ đỉnh đến cạnh đối diện với độ dài cạnh đối diện của đỉnh đó.

Lời giải:

a) Diện tích tam giác ABC là:

S=12bc=12ah⇒bc=ah⇒h=bca

b) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác ABC vuông tại A, ta có:

b2=a.b′⇒a=b2b′(1)c2=a.c′⇒a=c2c′(2)

Từ (1) và (2) suy ra: b2b′=c2c′.

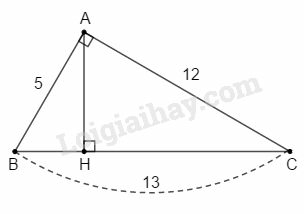
Bài 3 trang 195 SBT Toán 9 tập 2: Cho tam giác ABC có AB=5cm,AC=12cm và BC=13cm. Kẻ đường cao AH (H∈BC). Tính độ dài các đoạn thẳng BH và CH.

Phương pháp giải:

Sử dụng:

– Định lí Pytago đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

 

– Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:

+) AB2=BH.BC hay c2=a.c′.

+)AC2=CH.BC hay b2=ab′.

Lời giải:

Ta có:

AB2+AC2=52+122=169BC2=132=169⇒AB2+AC2=BC2

Theo định lí Pytago đảo thì tam giác ABC vuông tại A.

Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác ABC vuông tại A, ta có:

AB2=BC.BH

⇒BH=AB2BC=5213=2513=11213(cm)

CH=BC−BH=13−2513=14413=11113(cm)

Bài 4 trang 196 SBT Toán 9 tập 2: Tính sin, cos, tang của các góc A và B của tam giác ABC vuông ở C biết:

a) BC=8,AB=17;

b) BC=21,AC=20;

c) BC=1,AC=2;

d) AC=24,AB=25.

Phương pháp giải:

Sử dụng:

– Định lí Pytago: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

– Trong tam giác vuông các tỉ số lượng giác của góc nhọn (α) được định nghĩa như sau: 

 

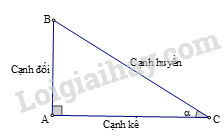
sin⁡α=ABBC;cos⁡α=ACBC;tan⁡α=ABAC;cot⁡α=ACAB. 

Lời giải:

a) Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:

AB2=BC2+AC2

⇒AC=AB2−BC2=172−82=15

Tam giác ABC vuông tại C nên A^ và B^ là hai góc phụ nhau, ta có:

sin⁡A=cos⁡B=BCAB=817cos⁡A=sin⁡B=CAAB=1517tan⁡A=cot⁡B=BCAC=815cot⁡A=tan⁡B=ACBC=158

b) Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:

AB2=BC2+AC2=212+202=841

⇒AB=841=29.

Tam giác ABC vuông tại C nên A^ và B^ là hai góc phụ nhau, ta có:

sin⁡A=cos⁡B=BCAB=2129cos⁡A=sin⁡B=ACAB=2029tan⁡A=cot⁡B=BCAC=2120cot⁡A=tan⁡B=ACBC=2021

c) Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:

AB2=BC2+AC2=12+22=5⇒AB=5

Tam giác ABC vuông tại C nên A^ và B^ là hai góc phụ nhau, ta có:

sin⁡A=cos⁡B=BCAB=15cos⁡A=sin⁡B=ACAB=25tan⁡A=cot⁡B=BCAC=12cot⁡A=tan⁡B=ACBC=21=2

d) Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:

AB2=BC2+AC2

⇒BC=AB2−AC2=252−242=49=7

Tam giác ABC vuông tại C nên A^ và B^ là hai góc phụ nhau, ta có:

sin⁡A=cos⁡B=BCAB=725cos⁡A=sin⁡B=ACAB=2425tan⁡A=cot⁡B=BCAC=724cot⁡A=tan⁡B=ACBC=247

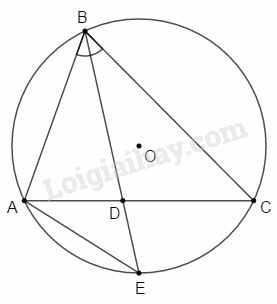
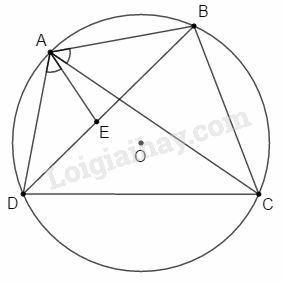
Bài 5 trang 196 SBT Toán 9 tập 2: BD là đường phân giác của tam giác ABC. Chứng minh rằng BD2=AB.BC−AD.DC.

Phương pháp giải:

Sử dụng:

– Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

– Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

Lời giải:

Gọi E là giao điểm của tia BD và đường tròn ngoại tiếp ΔABC.

* Xét ΔBEA và ΔBCD có:

ABE^=DBC^ (vì BD là tia phân giác B^)

BEA^=BCD^ (hai góc nội tiếp cùng chắn cung AB)

⇒ΔBEA∽ΔBCD (g.g)

⇒ABBD=BEBC

Mà BE=BD+DE nên ABBD=BD+DEBC

⇒BD2+BD.DE=AB.BC

⇒BD2=AB.BC−BD.DE    (1)

* Xét ΔBDC và ΔADE có:

BDC^=ADE^ (hai góc đối đỉnh)

DBC^=DAE^ (hai góc nội tiếp cùng chắn cung CE)

⇒ΔBDC∽ΔADE (g.g)

⇒BDDC=ADDE

⇒BD.DE=AD.DC          (2)

Từ (1) và (2) suy ra: BD2=AB.BC−AD.DC (điều phải chứng minh).

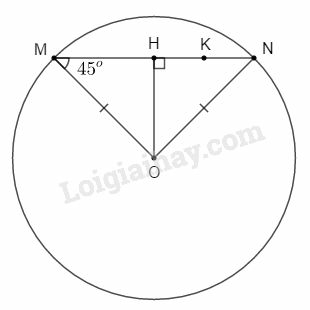
Bài 6 trang 196 SBT Toán 9 tập 2: Cho đường tròn (O). Khoảng cách từ O đến dây MN của đường tròn bằng 7cm, OMN^=45o. Trên dây MN lấy một điểm K sao cho MK=3KN (h.123). Độ dài đoạn MK là:

(A) 10,5cm;                          (B) 9cm;

(C) 14cm;                              (D) 12cm.

Hãy chọn đáp số đúng.

Phương pháp giải:

Sử dụng: Trong tam giác cân đường cao ứng với cạnh đáy đồng thời là đường trung tuyến, đường trung trực, đường phân giác.

Lời giải:

Gọi H là chân đường cao hạ từ O đến MN.

ΔOHM có OHM^=90o;OMH^=45o nên ΔOHM vuông cân tại H.

⇒MH=OH=7cm.

Lại có ΔOMN có OM=ON= bán kính nên ΔOMN cân tại O.

Do đó OH vừa là đường cao đồng thời là trung tuyến của ΔOMN.

⇒MH=NH=7cm.

Ta có: MN=MH+NH=7+7=14cm.

Mà MK=3KN nên MK=34MN=34.14=10,5(cm).

Chọn A.

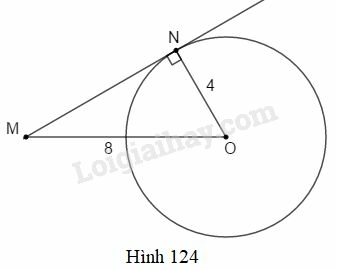
Bài 7 trang 196 SBT Toán 9 tập 2: Cho đường tròn (O;4cm) và một điểm M sao cho OM=8cm. Kẻ tiếp tuyến MN với đường tròn (O),N là tiếp điểm (h.124). Số đo của góc MON là:

(A) 45o;                                         (B) 90o;

(C) 30o;                                         (D) 60o.

Hãy chọn đáp số đúng.   

Phương pháp giải:

Sử dụng:

– Trong tam giác vuông các tỉ số lượng giác của góc nhọn (α) được định nghĩa như sau: 

 

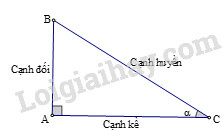
sin⁡α=ABBC;cos⁡α=ACBC;tan⁡α=ABAC;cot⁡α=ACAB. 

Lời giải:

Xét ΔOMN vuông tại N ta có:

cos⁡MON^=ONOM=12⇒MON^=60o

Chọn D.

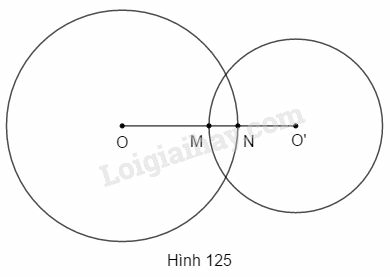
Bài 8 trang 196 SBT Toán 9 tập 2: Cho đường tròn (O;8cm) và đường tròn (O′;6cm) có đoạn nối tâm OO′=10cm. Đường tròn (O) cắt OO′ tại N, đường tròn (O′) cắt OO′ tại M (h.125). Độ dài MN bằng:

(A) 5cm;                         (B) 3cm;

(C) 6cm;                         (D) 4cm.

Hãy chọn đáp số đúng.

Phương pháp giải:

Ta có: OO′=ON+O′M−MN từ đó ta tính được MN.

Lời giải:

Ta có: 

OO′=ON+O′M−MN⇒MN=ON+O′M−OO′⇒MN=8+6−10=4(cm).

Chọn D.

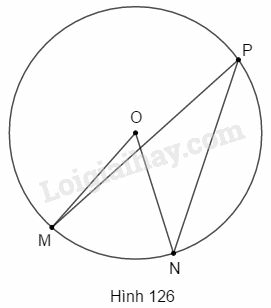
Bài 9 trang 196 SBT Toán 9 tập 2: Trên hình 126, số đo góc MPN nhỏ hơn số đo góc MON là 35o. Tổng số đo hai góc MPN và MON là:

(A) 90o;                                      (B) 105o;

(C) 115o;                                    (D) 70o.

Hãy chọn đáp số đúng.

Phương pháp giải:

Sử dụng: Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

Lời giải:

Xét đường tròn (O) có: 

MPN^=12MON^ (góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung).

⇒MON^=2MPN^

Mặt khác: 

MON^−MPN^=35o (gt)

⇒2MPN^−MPN^=35o

⇒MPN^=35o.

⇒MON^=2MPN^=2.35o=70o.

Vậy MON^+MPN^=70o+35o=105o.

Chọn B.

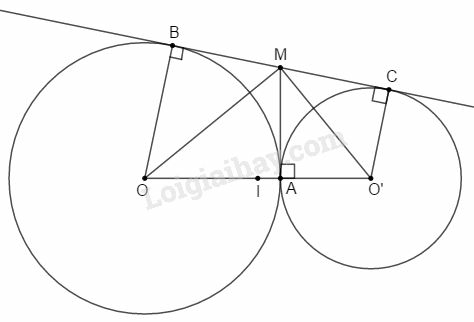
Bài 10 trang 197 SBT Toán 9 tập 2: Cho hai đường tròn (O;16cm) và (O′;9cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (B∈(O),C∈(O′)). Kẻ tiếp tuyến chung tại A cắt BC ở M.

a) Tính góc OMO′.

b) Tính độ dài BC.

c) Gọi I là trung điểm của OO′. Chứng minh rằng BC là tiếp tuyến của đường tròn tâm I, bán kính IM.

Phương pháp giải:

Sử dụng:

* Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

– Điểm đó cách đều hai tiếp điểm.

– Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

– Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm

* Trong tam giác vuông đường trung tuyến ứng với cạnh bằng nửa cạnh huyền.

* Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Lời giải:

a) MO là tia phân giác của AMB^ (tính chất hai tiếp tuyến cắt nhau).

⇒BMO^=OMA^=12AMB^

MO′ là tia phân giác của AMC^ (tính chất hai tiếp tuyến cắt nhau).

⇒CMO′^=O′MA^=12AMC^

Ta có: OMO′^=OMA^+O′MA^

⇒OMO′^=12AMB^+12AMC^=12(AMB^+AMC^)=12.180o=90o

b) Xét ΔOMO′ vuông tại M ta có:

MA2=OA.O′A=16.9=144⇒MA=144=12(cm).

Lại có MA=MB=MC (tính chất hai tiếp tuyến cắt nhau).

⇒MB=MC=12(cm).

⇒BC=MB+MC=12+12=24(cm).

c) 

OB⊥BCO′C⊥BC}⇒OB//O′C

Do đó tứ giác OBCO′ là hình thang.

Có MB=MC;IA=IB nên IM là đường trung bình của hình thang OBCO′. Do đó IM//OB//O′C.

Mà OB⊥BC nên IM⊥BC.

ΔOMO′ vuông tại M có IM là trung tuyến ứng với cạnh huyền nên IM=12OO′.

Do đó IM là bán kính của đường tròn tâm I lại vuông góc với BC tại M nên BC là tiếp tuyến của (I;IM).

Bài 11 trang 197 SBT Toán 9 tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O;R) có hai đường chéo AC và BD vuông góc với nhau. Chứng minh rằng AB2+CD2=4R2.

Phương pháp giải:

Sử dụng:

– Trên một đường tròn hai dây song song chắn hai cung bằng nhau.

– Hai cung bằng nhau căng hai dây bằng nhau.

– Định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.

Lời giải:

Kẻ đường kính BB′. Nối B′A,B′D,B′C.

B′DB^=90o (góc nội tiếp chắn nửa đường tròn).

⇒DB′⊥BD

Mặt khác AC⊥BD (gt)

⇒DB′//AC

Vì AC//DB′ nên  sđAD⏜nhỏ=sđB′C⏜nhỏ

sđADB′⏜=sđAD⏜nhỏ+sđDB′⏜nhỏ

sđCB′D⏜=sđB′C⏜nhỏ+sđDB′⏜nhỏ

Mà  sđAD⏜nhỏ=sđB′C⏜nhỏ

⇒sđADB′⏜=sđCB′D⏜.

⇒AB′=CD (các dây cung chắn các cung bằng nhau thì bằng nhau)    (1)

Ta có BAB′^=90o (góc nội tiếp chắn nửa đường tròn).

Áp dụng định lí Pytago vào tam giác vuông BAB′ có:

AB2+AB′2=BB′2        (2)

Từ (1) và (2) suy ra: AB2+CD2=BB′2

Hay AB2+CD2=4R2.

Bài 12 trang 197 SBT Toán 9 tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O). Trên đường chéo BD lấy điểm E sao cho DAE^=BAC^. Chứng minh:

a) ΔADE∽ΔACB,ΔABE∽ΔACD;

b) AD.BC+AB.CD=AC.BD.

Phương pháp giải:

Sử dụng:

– Các góc nội tiếp chắn cùng một cung hoặc chắn các cung bằng nhau thì bằng nhau.

– Hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

Lời giải:

a) Xét ΔADE và ΔACB có:

ADE^=ACB^ (hai góc nội tiếp cùng chắn cung nhỏ AB)

DAE^=CAB^ (gt)

⇒ΔADE∽ΔACB (g.g)

Ta có:

BAE^=BAC^+CAE^CAD^=DAE^+CAE^

Mà BAC^=DAE^ (gt) nên BAE^=CAD^

Xét ΔABE và ΔACD có:

BAE^=CAD^ (chứng minh trên)

ABE^=ACD^ (hai góc nội tiếp cùng chắn cung nhỏ AD)

⇒ΔABE∽ΔACD (g.g).

b) Vì ΔADE∽ΔACB (câu a) suy ra ADAC=DECB

⇒AD.CB=AC.DE     (1)

Vì ΔABE∽ΔACD (câu a) suy ra ABAC=BECD

⇒AB.CD=AC.BE     (2)

Từ (1) và (2) ta có:

AD.CB+AB.CD=AC.DE+AC.BE=AC.(DE+BE)=AC.BD.

Vậy AD.BC+AB.CD=AC.BD.

 

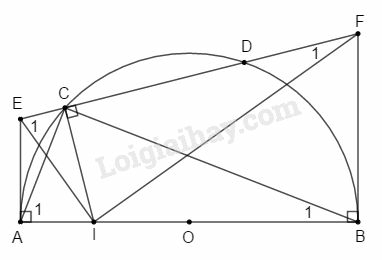
Bài 13 trang 197 SBT Toán 9 tập 2: Cho nửa đường tròn đường kính AB và một dây CD. Qua C vẽ đường thẳng vuông góc với CD, cắt AB tại I. Các tiếp tuyến tại A và B của nửa đường tròn cắt đường thẳng CD theo thứ tự tại E và F. Chứng minh rằng:

a) Các tứ giác AECI và BFCI nội tiếp được;

b) Tam giác IEF vuông.

Phương pháp giải:

Sử dụng:

– Nếu tứ giác có tổng số đo hai góc đối diện bằng 180o thì tứ giác đó nội tiếp được đường tròn.

– Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

– Hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

Lời giải:

a)

Tứ giác AECI có EAI^+ECI^=90o+90o=180o do đó tứ giác AECI nội tiếp được.

Tứ giác BFCI có FCI^+IBF^=90o+90o=180o do đó tứ giác BFCI nội tiếp được.

b) Xét ΔIEF và ΔCAB có:

E1^=A1^ (hai góc nội tiếp cùng chắn cung CI của đường tròn ngoại tiếp tứ giác AECI)

F1^=B1^ (hai góc nội tiếp cùng chắn cung CI của đường tròn ngoại tiếp tứ giác BFCI)

⇒ΔIEF∽ΔCAB (g.g).

⇒EIF^=ACB^ (hai góc tương ứng).

Ta lại có ACB^=90o (góc nội tiếp chắn nửa đường tròn).

⇒EIF^=90o.

Vậy tam giác IEF vuông tại I.

Bài 14 trang 197 SBT Toán 9 tập 2: Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng:

a) Các tứ giác ABEF,DCEF nội tiếp được;

b) Tia CA là tia phân giác của góc BCF;

c) Tứ giác BCMF nội tiếp được.

Phương pháp giải:

Sử dụng:

– Nếu tứ giác có tổng số đo hai góc đối diện bằng 180o thì tứ giác đó nội tiếp được đường tròn.

– Trên một đường tròn các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

– Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc α thì nội tiếp được.

Lời giải:

a) Ta có ABD^=ACD^=90o (góc nội tiếp chắn nửa đường tròn).

Tứ giác ABEF có ABE^+AFE^=90o+90o=180o nên tứ giác ABEF nội tiếp được.

Tứ giác DCEF có DCE^+DFE^=90o+90o=180o nên tứ giác DCEF nội tiếp được.

b) C1^=D1^ (hai góc nội tiếp cùng chắn cung nhỏ AB)   (1)

C2^=D1^ (hai góc nội tiếp cùng chắn cung EF của đường tròn ngoại tiếp tứ giác DCEF)   (2)

Từ (1) và (2) ta có C1^=C2^.

Vậy CA là tia phân giác của góc BCF.

c) ΔDEF vuông tại F có FM là đường trung tuyến ứng với cạnh huyền nên FM=MD=ME=12DE.

⇒ΔDMF cân tại M.

⇒D1^=MFD^ (tính chất tam giác cân).

BMF^ là góc ngoài tại đỉnh M của ΔDMF nên:

BMF^=D1^+MFD^=2D1^    (3)

Theo câu b) ta có: BCF^=C1^+C2^=2D1^      (4)

Từ (3) và (4) suy ra BMF^=BCF^.

Vậy C và M cùng nhìn BF dưới một góc bằng nhau nên tứ giác BCMF nội tiếp được.

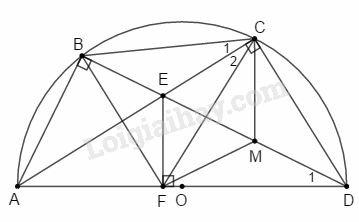
Bài 15 trang 197 SBT Toán 9 tập 2: Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA,MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD,CE,CF lần lượt vuông góc với AB,MA,MB. Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng:

a) Các tứ giác AECD,BFCD nội tiếp được;

b) CD2=CE.CF;

c) Tứ giác ICKD nội tiếp được;

d) IK⊥CD.

Phương pháp giải:

Sử dụng:

– Nếu tứ giác có tổng số đo hai góc đối diện bằng 180o thì tứ giác đó nội tiếp được đường tròn.

– Trên một đường tròn các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

Lời giải:

a) Ta có AEC^+ADC^=90o+90o=180o nên tứ giác AECD nội tiếp được.

Ta có BFC^+BDC^=90o+90o=180o nên tứ giác BFCD nội tiếp được.

b) Có D1^=A1^ (hai góc nội tiếp cùng chắn cung EC của đường tròn ngoại tiếp tứ giác AECD)  (1)

A1^=B1^ (góc giữa tia tiếp tuyến với một dây cung và góc nội tiếp cùng chắn cung AC của đường tròn tâm O)    (2)

B1^=F1^ (hai góc nội tiếp cùng chắn cung CD của đường tròn ngoại tiếp tứ giác BFCD)     (3)

Từ (1), (2) và (3) suy ra: D1^=F1^.

Có E2^=A2^ (hai góc nội tiếp cùng chắn cung CD của đường tròn ngoại tiếp tứ giác AECD)  (4)

B2^=A2^ (góc giữa tia tiếp tuyến với một dây cung và góc nội tiếp cùng chắn cung BC của đường tròn tâm O)    (5)

B2^=D2^ (hai góc nội tiếp cùng chắn cung CF của đường tròn ngoại tiếp tứ giác BFCD)     (6)

Từ (4), (5) và (6) suy ra: E2^=D2^.

Xét ΔDEC và ΔFDC có:

D1^=F1^ (chứng minh trên)

E2^=D2^ (chứng minh trên)

⇒ΔDEC∽ΔFDC (g.g).

⇒CDCF=CECD⇒CD2=CE.CF

c) Tứ giác ICKD có:

ICK^+IDK^=ICK^+D1^+D2^=ICK^+B1^+A2^=180o.

Suy ra tứ giác ICKD nội tiếp được.

d) Ta có CIK^=D2^ (hai góc nội tiếp cùng chắn cung CK của đường tròn ngoại tiếp tứ giác ICKD).

⇒CIK^=A2^, mà CIK^ và A2^ ở vị trí đồng vị nên IK//AB.

Mặt khác CD⊥AB (gt) nên CD⊥IK.

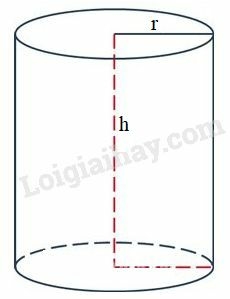
Bài 16 trang 197 SBT Toán 9 tập 2: Một hình trụ có đường cao bằng đường kính đáy. Biết rằng thể tích hình trụ là 128πcm3. Tính diện tích xung quanh của nó.

Phương pháp giải:

Sử dụng:

– Công thức tính diện tích xung quanh hình trụ: Sxq=2πrh.

– Công thức tính thể tích hình trụ: V=Sh=πr2h.

(r là bán kính đường tròn đáy, h là chiều cao, S là diện tích đáy).

Lời giải:

Hình trụ có đường cao bằng đường kính đáy nên h=2r.

Theo đề bài ta có:

V=πr2h=π.r2.2r=2πr3=128π⇒r3=64⇒r=4(cm).

Suy ra h=2r=2.4=8(cm)

Diện tích xung quanh của hình trụ là:

Sxq=2πr.h=2π.4.8=64π(cm2).

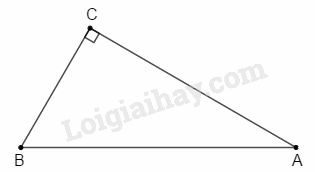
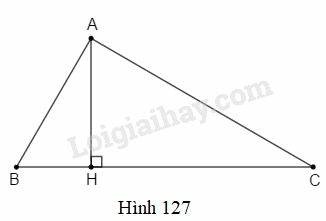
Bài 17 trang 198 SBT Toán 9 tập 2: Cho hình 127. Khi quay tam giác ABC một vòng quanh cạnh BC cố định thì được:

(A) một hình nón;

(B) hai hình nón;

(C) một hình trụ;

(D) một đường tròn.

Hãy chọn câu trả lời đúng.

Phương pháp giải:

Khi quay tam giác ABC một vòng quanh cạnh  cố định thì được hai hình nón có chung đáy và bán kính đáy là AH.

Lời giải:

Khi quay tam giác ABC một vòng quanh cạnh BC cố định thì được hai hình nón có chung đáy và bán kính đáy là AH.

Chọn B.

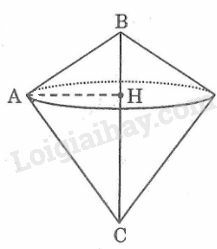
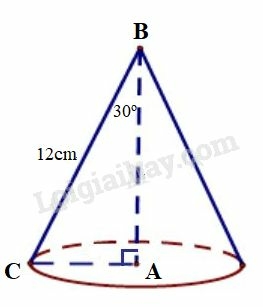
Bài 18 trang 198 SBT Toán 9 tập 2: Quay tam giác vuông ABC (A^=90o) một vòng quanh cạnh AB là được một hình nón. Tính thể tích và diện tích xung quanh của hình nón biết BC=12cm và ABC^=30o.

Phương pháp giải:

Áp dụng công thức:

– Diện tích xung quanh của hình nón: Sxq=πrl.

– Thể tích hình nón: V=13πr2h.

(r là bán kính đường tròn đáy, l là đường sinh, h là chiều cao).

Lời giải:

Xét ΔABC vuông tại A, ta có:

AB=BC.cos⁡B=BC.cos⁡30o=12.32=63(cm).

AC=BC.sin⁡B=BC.sin⁡30o=12.12=6(cm).

Quay tam giác vuông ABC một vòng quanh cạnh AB ta được một hình nón có chiều cao AB, bán kính đường tròn đáy là AC và đường sinh BC.

Diện tích xung quanh của hình nón tạo thành là:

Sxq=π.AC.BC=π.6.12=72π(cm2).

Thể tích của hình nón tạo thành là:

V=13.π.AC2.AB=13.π.62.63=723π(cm3).