tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Ôn tập chương 1: Hệ thức lượng trong tam giác vuông chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Ôn tập chương 1: Hệ thức lượng trong tam giác vuông
a) cosα=513;
b) cosα=1517;
c) cosα=0,6.
Phương pháp giải:
Áp dụng kiến thức:
1) sin2α+cos2α=1
2) tanα=sinαcosα
Lời giải:
a) cosα=513
* Ta có:
sin2α+cos2α=1
Suy ra:
sin2α=1−cos2α=1−(513)2=1−25169=144169
Vì sinα>0 nên sinα=144169=1213
* tanα=sinαcosα=1213513=1213.135=125
b) cosα=1517
* Ta có: sin2α+cos2α=1
Suy ra:
sin2α=1−cos2α=1−(1517)2=1−225289=64289
Vì sinα>0 nên sinα=64289=817
* tanα=sinαcosα=8171517=817.1715=815
c) cosα=0,6
* Ta có: sin2α+cos2α=1.
Suy ra: sin2α=1−cos2α
=1−(0,6)2=1−0,36=0,64
Vì sinα>0 nên sinα=0,64=0,8
* tanα=sinαcosα=0,80,6=86=43
a) 1−sin2α;
b) (1−cosα)(1+cosα);
c) 1+sin2α+cos2α;
d) sinα−sinα.cos2α;
e) sin4α+cos4α+2.sin2α.cos2α;
g) tan2α−sin2α.tan2α;
h) cos2α+tan2α.cos2α;
i) tan2α(2.cos2α+sin2α−1).
Phương pháp giải:
Áp dụng các kiến thức:
1) sin2α+cos2α=1
2) tan2α=sin2αcos2α
Lời giải:
a)
1−sin2α=(sin2α+cos2α)−sin2α
=sin2α+cos2α−sin2α=cos2α
b)
(1−cosα)(1+cosα)=1−cos2α=(sin2α+cos2α)−cos2α
=sin2α+cos2α−cos2α=sin2α
c)
1+sin2α+cos2α=1+(sin2α+cos2α)=1+1=2
d)
sinα−sinα.cos2α=sinα(1−cos2α)
=sinα[(sin2α+cos2α)−cos2α]
=sinα(sin2α+cos2α−cos2α)
=sinα.sin2α=sin3α
e)sin4α+cos4α+2.sin2α.cos2α=(sin2α+cos2α)2=12=1
g) tan2α−sin2α.tan2α=tan2α(1−sin2α)
=tan2α.[(sin2α+cos2α)−sin2α]
=tan2α.cos2α=sin2αcos2α.cos2α=sin2α
h)cos2α+tan2α.cos2α=cos2α+sin2αcos2α.cos2α=cos2α+sin2α=1
i)
tan2α(2.cos2α+sin2α−1)
=tan2α.[cos2α+(cos2α+sin2α)−1]
=tan2α.(cos2α+1−1)=tan2α.cos2α
=sin2αcos2α.cos2α=sin2α
Lời giải:
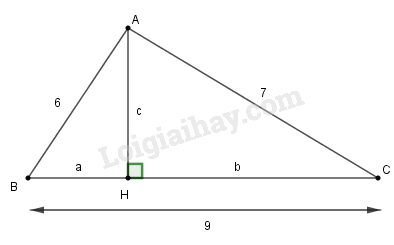
Gọi độ dài đường cao là c, hình chiếu của hai cạnh 6 và 7 trên cạnh có độ dài bằng 9 lần lượt là a và b.
Ta có: a<b ( vì 6<7)
Theo định lí Pi-ta-go, ta có:
c2=62−a2=36−a2
c2=72−b2=49−b2
Suy ra: 36−a2=49−b2
⇔b2−a2=49−36
⇔(b+a)(b−a)=13
Mà a+b=9 (*) nên:
9.(b−a)=13⇔b−a=139⇒b=a+139
Thay vào (*), ta có:
a+a+139=9⇔2a+139=9
⇔a=9−1392=349
Suy ra: b=9−a=9−349=479
c=49−(479)2≈4,7
cạnh bên có độ dài là 6.
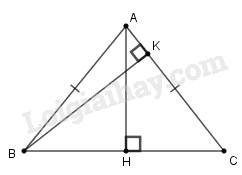
Phương pháp giải:
Áp dụng tính chất về cạnh và đường cao của tam giác cân.
Vận dụng định lí Py-ta-go vào các tam giác vuông.
Lời giải:
Giả sử ∆ABC cân tại A có AH⊥BC,AH=5,BK⊥AC,BK=6.
Vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến. Suy ra HB=HC=12BC (tính chất tam giác cân)
SABC=12AH.BC=12BK.AC=12.5.BC=12.6.AC
Suy ra: 5BC=6AC⇒BC=65AC(1)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACH, ta có:
AC2=AH2+HC2=52+(BC2)2=25+BC24(2)
Từ (1) và (2) suy ra:
AC2=25+36AC2254=2500100+36AC2100
Suy ra:
100AC2=2500+36AC2
⇔64AC2=2500⇔8AC=50⇒AC=6,25
Vậy BC=65.6,25=7,5.
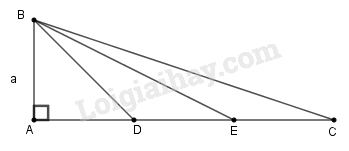
a) Chứng minh: DEDB=DBDC
b) Chứng minh ∆BDE đồng dạng ∆CDB
c) Tính tổng AEB^+BCD^ bằng hai cách
Cách 1: Sử dụng kết quả ở câu b);
Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.
Phương pháp giải:
– Áp dụng định lí Py-ta-go trong tam giác vuông.
– Các trường hợp bằng nhau của tam giác.
– Sử dụng: Trong tam giác ABC vuông tại A thì tanACB^=ABAC
Lời giải:
a) Ta có: AD=DE=EC=AC3=a
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
BD2=AD2+AB2=a2+a2=2a2
Suy ra: BD=a2
Ta có:
DEDB=aa2=22;DBDC=a22a=22
Vậy DEDB=DBDC
b) Xét ∆BDE và ∆CDB, ta có:
DEDB=DBDC (1)
BDE^=BDC^ (2)
Từ (1) và (2) suy ra ∆BDE đồng dạng ∆CDB (c-g-c).
c) * Cách 1:
Ta có: ∆BDE đồng dạng ∆CDB ⇒BED^=CBD^
Mặt khác:
AEB^+BCD^=BED^+BCD^=CBD^+BCD^ (3)
Trong ∆BCD, ta có:
ADB^=CBD^+BCD^ (tính chất góc ngoài) (4)
Lại có: ADB^=45∘ (vì ∆ABD vuông cân tại A) (5)
Từ (3), (4) và (5) suy ra: AEB^+BCD^=45∘
* Cách 2:
Ta có: AE=AD+DE=2a
Trong tam giác ABE, ta có:
tanAEB^=ABAE=a2a=12
Suy ra: AEB^=26∘34′
Trong tam giác vuông ABC, ta có:
tanACB^=ABAC=a3a=13
Suy ra: ACB^=18∘26′
Suy ra AEB^+ACB^=26∘34′+18∘26′=450
Vậy AEB^+ACB^=AEB^+BCD^=45∘
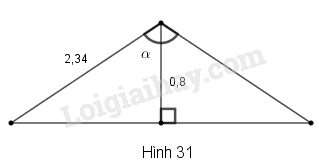
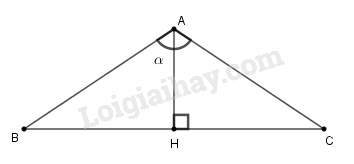
Vận dụng kiến thức :
Trong tam giác ABH vuông tại H thì , từ đó tìm độ lớn góc .
Lời giải:
Hai mái nhà bằng nhau tạo thành hai cạnh AB, AC của một tam giác cân ABC (hình vẽ). Chiều cao AH của tam giác ABC cũng là đường phân giác của tam giác. Khi đó ta có: BAH^=BAC^2=α2
Xét tam giác ABH vuông tại H, ta có:
cosα2=AHAB=0,82,34≈0,3419
Bấm máy tính: SHIFT cos 0,3419 =
Suy ra: α2≈70∘
Vậy α≈140∘.
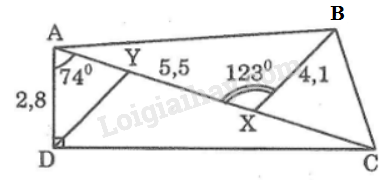
Biết:
AD⊥DC,DAC^=74∘
AXB^=123∘,AD=2,8cm; AX=5,5cm,BX=4,1cm.
a) Tính AC.
b) Gọi Y là điểm trên AX sao cho DY⁄⁄BX. Hãy tính XY
c) Tính diện tích tam giác BCX.
Phương pháp giải:
Áp dụng các hệ thức lượng trong tam giác vuông.
Lời giải:
a) Trong tam giác vuông ACD, ta có:
AC=ADcosCAD^=2,8cos74∘≈10,158(cm)
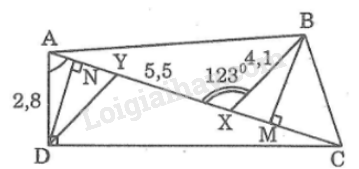
b) Kẻ DN⊥AC
Trong tam giác vuông AND, ta có:
DN=AD.sinDAN^=2,8.sin74∘≈2,692(cm)
AN=AD.cosDAN^=2,8.cos74∘≈0,772(cm)
Vì BX//DY nên DYX^=BXY^=123∘ ( hai góc so le trong)
Mà DYN^+DYX^=180∘ (kề bù)
Suy ra:
DYN^=180∘−DYX^=180∘−123∘=57∘
Trong tam giác vuông DYN, ta có:
NY=DN.cotDYN^≈2,692.cot57∘≈1,748(cm)
Ta có:
XY=AX−(AN+NY)=5,5−(0,772+1,748)=2,98cm
c) Ta có:
CX=AC−AX≈10,158−5,5=4,658(cm)
Kẻ BM⊥CX
Ta có:
BXC^=180∘−BXA^=180∘−123∘=57∘
Trong tam giác vuông BMX, ta có:
BM=BX.sinBXC^=4,1.sin57∘≈3,439(cm)
SBCX=12BM.CX=12.3,439.4,658≈8,009(cm2).
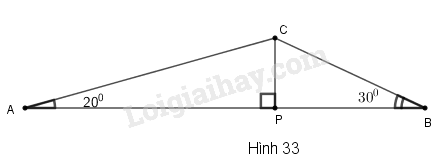
Hãy tìm:
a) AP, BP;
b) CP.
Phương pháp giải:
Áp dụng kiến thức về hệ thức lượng trong tam giác vuông.
cot α = cạnh kề : cạnh đối.
Lời giải:
a) Trong tam giác vuông ACP, ta có:
AP=CP.cotPAC^(1)
Trong tam giác vuông BCP, ta có:
BP=CP.cotPBC^(2)
Từ (1) và (2) suy ra:
(AP+BP)=CP.cotPAC^+CP.cotPBC^
Hay AB=CP(cotPAC^+cotPBC^)
Suy ra:
CP=ABcotPAC^+cotPBC^=ABcot20∘+cot30∘≈13,394(cm)
b) Thay CP=13,394 vào (1) ta có:
AP=13,394.cot20∘≈36,801(cm)
Thay CP=13,394 vào (2) ta có:
BP=13,394.cot30∘≈23,199(cm)
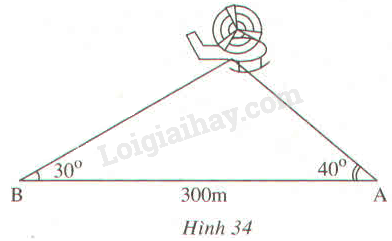
Phương pháp giải:
Áp dụng tỉ số giữa cạnh kề và cạnh đối trong tam giác vuông.
Lời giải:
Gọi C là vị trí của máy bay.
Kẻ CH⊥AB
Trong tam giác vuông ACH, ta có:
AH=CH.cotA^(1)
Trong tam giác vuông BCH, ta có:
BH=CH.cotB^(2)
Từ (1) và (2) suy ra:
AH+BH=CH.cotA^+CH.cotB^
Hay AB=CH.(cotA^+cotB^)
Suy ra:
CH=ABcotA^+cotB^=ABcot40∘+cot30∘≈102,61(m)
– Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
– Chu vi hình thang bằng tổng độ dài các cạnh bao quanh của hình đó.
– Diện tích hình thang bằng đáy lớn cộng đáy bé (cùng đơn vị đo) chia 2 rồi nhân với chiều cao.
Lời giải:
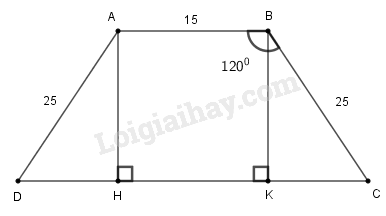
Giả sử hình thang ABCD có đáy nhỏ AB=15cm, cạnh bên AD=BC=25cm, ABC^=BAD^=120∘.
Kẻ AH⊥CD,BK⊥CD
Ta có: AB//HK và AH//BK (cùng vuông với CD) nên ABKH là hình bình hành.
Suy ra: HK=AB=15(cm) và AH=BK
Vì AB//CD nên ADC^+DAB^=180∘ (hai góc trong cùng phía)
Suy ra:
ADC^=180∘−DAB^=180∘−120∘=60∘
Trong tam giác vuông ADH, ta có:
DH=AD.cosADC^=25.cos60∘=12,5(cm)
AH=AD.sinADC^=25.sin60∘=2532(cm)
Ta có: AH=BK (cmt) và AD=BC (gt) nên hai tam giác vuông ∆ADH=∆BCK (cạnh huyền – cạnh góc vuông)
Suy ra: CK=DH=12,5(cm)
Ta có: CD=CK+KH+HD=12,5+15+12,5=40cm
Chu vi hình thang ABCD là:
AB+BC+CD+DA
=15+25+40+25
=105(cm)
Diện tích hình thang ABCD là:
SABCD=AB+CD2.AH=15+402.2522≈595,392(cm2)
a) Tính BC,B^,C^;
b) Phân giác của góc A cắt BC tại D. Tính BD,CD.
c) Từ D kẻ DE và DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích của tứ giác AEDF.
Phương pháp giải:
a) Áp dụng định lí Py-ta-go và tỉ số lượng giác.
b) Vận dụng tính chất đường phân giác tìm độ dài cạnh BD.
c) Áp dụng dấu hiệu nhận biết các hình tứ giác đã học.
Tính chu vi và diện tích của tứ giác.
Lời giải:
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+82=36+64=100(cm)
Suy ra: BC=100=10(cm)
Xét tam giác vuông ABC, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: sinC=ABAC=610=0,6
Suy ra: C^=36∘52′
Ta có: B^+C^=90∘ (vì tam giác ABC vuông tại A)
⇒B^=90∘−C^=90∘−36∘52′=53∘8′
b) Vì AD là đường phân giác của tam giác ABC, nên:
BDDC=ABAC (tính chất đường phân giác)
Suy ra: BDBD+DC=ABAB+AC
⇒BDBC=ABAB+AC
Suy ra: BD=BC.ABAB+AC=10.66+8=307(cm)
DC=BC−BD=10−307=407
c) Ta có: A^=AED^=AFD^=900
Suy ra tứ giác AEDF có ba góc vuông nên hình đó là hình chữ nhật.
Mặt khác, D nằm trên tia phân giác của góc A nên DE=DF (tính chất tia phân giác của 1 góc)
Vậy tứ giác AEDF là hình vuông.
Vì DE⊥AB,AC⊥AB nên DE//AC
Theo định lí Ta-lét trong tam giác BAC, ta có:
CDBC=AEAB⇒AE=CD.ABBC=407.610=247
Chu vi tứ giác AEDF bằng: 4AE=4.247=967(cm)
Diện tích tứ giác AEDF bằng: AE2=(247)2=57649(cm2)
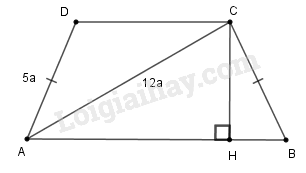
a) Tính sinB+cosBsinB−cosB.
b) Tính chiều cao của hình thang ABCD.
Phương pháp giải:
a) Áp dụng định lí Py-ta-go và tỉ số lượng giác.
b) Chiều cao hình thang ABCD bằng chiều cao tam giác ABC, áp dụng tỉ số lượng giác, tìm chiều cao của tam giác ABC.
Lời giải:
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AB2=BC2+AC2=(5a)2+(12a)2=169a2
Suy ra: AB=169a2=13a
Xét tam giác vuông ABC, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
sinB^=ACAB=12a13a=1213
cosB^=BCAB=5a13a=513
Suy ra:
sinB^+cosB^sinB^−cosB^=1213+5131213−513=1713713=1713.137=177
b) Kẻ CH⊥AB
Trong tam giác vuông BCH, ta có:
CH=CB.sinB^=5a.1213=60a13
a) Tính các góc của tam giác ABC.
b) Tính diện tích tứ giác ABCD.
Phương pháp giải:
a) Áp dụng tỉ số lượng giác của góc nhọn và định lí Py-ta-go vào các tam giác vuông.
b) Áp dụng định lí Py-ta-go và kiến thức về đường trung bình của tam giác.
Lời giải:
a) Vì tam giác ABC cân tại A có AH⊥BC nên AH cũng là đường trung tuyến, suy ra: HB=HC=BC2=8(cm)
Trong tam giác vuông ABH, ta có:
cosB^=HBAB=810=0,8
Suy ra: B^≈36∘52′
Vì ∆ABC cân nên B^=C^=36∘52′
Ta có: A^+B^+C^=180∘ (tổng 3 góc trong tam giác ABC)
A^=180∘−(B^+C^)=180∘−(36∘52′+36∘52′)=106∘16′
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:
AB2=AH2+BH2⇒AH2=AB2−BH2=102−82=36
Suy ra: AH=6(cm)
Ta có: AI=13.AH=13.6=2(cm)
Suy ra: IH=AH−AI=6−2=4(cm)
Vì IH⊥BC và DC⊥BC nên IH//DC (1)
Mặt khác: BH=HC (cmt) (2)
Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD.
Suy ra: IH=12CD hay CD=2.IH=2.4=8(cm)
Ta có:
SABH=12AH.BH=12.6.8=24(cm2)
Vì AH//DC nên AHCD là hình thang và AH⊥HC nên HC là chiều cao của hình thang AHCD. Từ đó:
SAHCD=AH+CD2.HC=6+82.8=56(cm2)
Vậy SABCD=SABH+SAHCD=24+56=80 (cm2)
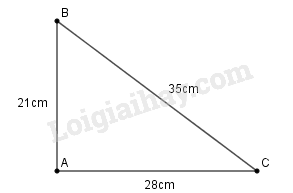
a) Chứng minh tam giác ABC vuông.
b) Tính sinB, sinC.
Phương pháp giải:
a) Áp dụng định lí Py-ta-go đảo.
b) Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải:
a) Ta có: AB2=212=441
AC2=282=784
BC2=352=1225
Vì AB2+AC2=441+784=1225=BC2 nên tam giác ABC vuông tại A ( theo định lí đảo Pi-ta-go).
b) Xét tam giác ABC vuông tại A, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
sinB^=ACBC=2835=45=0,8
sinC^=ABBC=2135=35=0,6
a) Chứng minh tanC^=1.
b) Tính tỉ số diện tích tam giác DBC và diện tích hình thang ABCD.
c) Tính tỉ số diện tích tam giác ABC và diện tích tam giác BCD.
Phương pháp giải:
Vận dụng kiến thức :
– Tứ giác có ba góc vuông và hai cạnh kề bằng nhau là hình vuông.
– Công thức tính diện tích tam giác và hình thang.
– Tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải:
a) Kẻ BH⊥CD
Ta có: AB//CD nên A^+ADC^=1800 (hai góc trong cùng phía bù nhau) và A^=90∘ (gt)
Suy ra: ADC^=90∘
Từ đó, tứ giác ABHD có ba góc vuông nên là hình chữ nhật. Mà AB=AD=a nên ABHD là hình vuông.
Suy ra: DH=BH=AB=a
Ta có: CD=DH+HC
Suy ra: HC=CD–DH=2a–a=a
Vậy tanC^=BHCH=aa=1
b) Ta có: SBCD=12BH.CD=12a.2a=a2 (đvdt)
SABCD=AB+CD2.AD=a+2a2.a=32a2 (đvdt)
Vậy SBCDSABCD=a232a2=132=23.
c) Diện tích tam giác ADC vuông tại D là: SADC=12AD.DC=12a.2a=a2 (đvdt)
Mà SABCD=32a2 (theo câu b)
Ta có: SABC=SABCD−SADC=32a2−a2=12a.a=12a2 (đvdt)
Vậy SABCSBCD=12a2a2=12
(với đvdt: đơn vị diện tích)
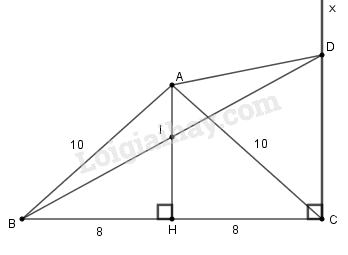
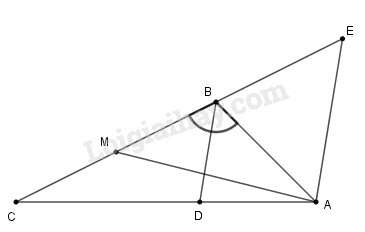
a) Tính độ dài đường phân giác BD.
b) Gọi M là trung điểm của BC. Chứng minh AM⊥BD.
Phương pháp giải:
– Vận dụng định lí Ta-lét trong tam giác.
– Chứng minh tam giác ABM cân tại B.
Lời giải:
a) Vì BD là tia phân giác của góc ABC nên:
ABD^=CBD^=ABC^2=120∘2=60∘
Từ A kẻ đường thẳng song song với BD cắt CB tại E.
Lại có:
BAE^=ABD^=60∘ (so le trong)
AEB^=CBD^=60∘ (đồng vị)
Suy ra tam giác ABE đều (vì có 2 góc bằng 600)
⇒AB=BE=EA=6(cm)(1)
Khi đó: CE=BC+BE=12+6=18(cm)
Tam giác ACE có AE//BD nên theo hệ quả định lý Ta-lét ta suy ra:
BCCE=BDAE
⇒BD=BC.AECE=12.618=4(cm)
b) Vì M là trung điểm cạnh BC nên ta có:
MB=MC=12.BC=12.12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM
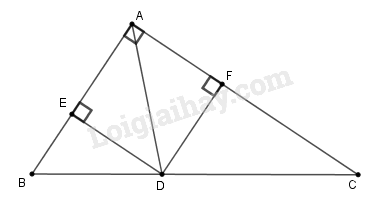
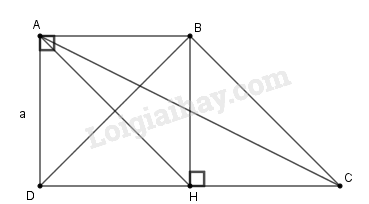
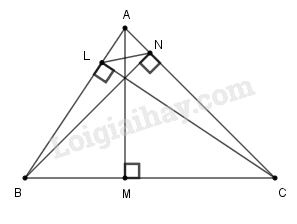
a) Tính độ dài đoạn thẳng DE.
b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH.
c) Tính diện tích tứ giác DENM.
Phương pháp giải:
a) Áp dụng tính chất hình chữ nhật và hệ thức lượng giữa đường cao và hình chiếu trong tam giác vuông.
b) Áp dụng tính chất của hình chữ nhật và tam giác cân.
c) Nhẩm lại dấu hiệu nhận biết hình thang và cách tính diện tích của hình đó.
Lời giải:
a) Ta có:
HD⊥AB⇒ADH^=90∘
HE⊥AC⇒AEH^=90∘
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật.
Suy ra: AH=DE (tính chất hình chữ nhật)
Tam giác ABC vuông tại A và có AH là đường cao.
Theo hệ thức liên hệ giữa đường cao và hình chiếu ta có:
AH2=HB.HC=4.9=36⇒AH=6(cm)
Vậy DE=6(cm)
b) * Gọi G là giao điểm của AH và DE
Ta có: GA=GD=GH=GE (tính chất hình chữ nhật ADHE)
Suy ra tam giác GHD cân tại G
Ta có:
GDH^=GHD^(1)
GDH^+MDH^=90∘(2)
GHD^+MHD^=90∘(3)
Từ (1), (2) và (3) suy ra: MDH^=MHD^(4)
Suy ra tam giác MDH cân tại M ⇒MD=MH(5)
Lại có: MDH^+MDB^=90∘(6)
MBD^+MHD^=90∘ (∆BDH vuông tại D) (7)
Từ (4), (6) và (7) suy ra: MDB^=MBD^
Suy ra tam giác MBD cân tại M ⇒MB=MD(8)
Từ (5) và (8) suy ra: MB=MH hay M là trung điểm của BH.
*Tam giác GHE cân tại G (do GH=GE (cmt))
Ta có: GHE^=GEH^(9)
GHE^+NHE^=90∘ (10)
GEH^+NEH^=90∘ (11)
Từ (9), (10) và (11) suy ra: NHE^=NEH^ (12)
Suy ra tam giác NEH cân tại N ⇒NE=NH (13)
Lại có: NEC^+NEH^=90∘ (14)
NHE^+NCE^=90∘ (∆CEH vuông tại E) (15)
Từ (12), (14) và (15) suy ra: NEC^=NCE^
Suy ra tam giác NCE cân tại N ⇒NC=NE(16)
Từ (13) và (16) suy ra: NC=NH hay N là trung điểm của CH.
c) Tam giác BDH vuông tại D có DM là đường trung tuyến nên:
DM=12BH=12.4=2(cm)
Tam giác CEH vuông tại E có EN là đường trung tuyến nên
EN=12CH=12.9=4,5(cm)
Mà MD⊥DE và NE⊥DE nên MD//NE
Suy ra tứ giác DENM là hình thang
Vậy
SDENM=DM+NE2.DE=2+4,52.6=19,5cm2.
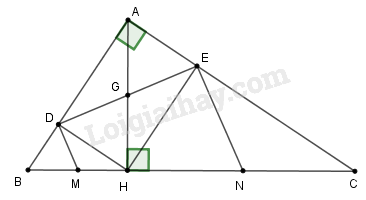
a) Tính AB,AC.
b) Từ A kẻ AM,AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B.
Chứng minh: MN//BC và MN=AB.
c) Chứng minh hai tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng.
Phương pháp giải:
Vận dụng kiến thức :
a) Tỉ số lượng giác của góc nhọn trong tam giác vuông.
b) Dấu hiệu nhận biết và tính chất của hình chữ nhật.
c) Các trường hợp đồng dạng của tam giác.
Lời giải:
a) Trong tam giác vuông ABC, ta có:
AB=BC.sinC^=10.sin30∘=10.12=5(cm)
AC=BC.cosC^=10.cos30∘=10.32=53(cm)
b) Ta có:
BM⊥BN (hai tia phân giác của 2 góc kề bù thì vuông góc với nhau) ⇒MBN^=90∘(1)
AM⊥BM (gt) ⇒AMB^=90∘(2)
AN⊥BN (gt) ⇒ANB^=90∘(3)
Từ (1), (2) và (3) suy ra tứ giác AMBN là hình chữ nhật.
Suy ra AM=BN,BM=AN,AB=MN (tính chất hình chữ nhật)
Suy ra: ∆AMB=∆NBM (c.g.c)
⇒ABM^=NMB^
Mà ABM^=MBC^(gt)
Suy ra: NMB^=MBC^
Suy ra MN//BC (có cặp so le trong bằng nhau)
Vì AMBN là hình chữ nhật nên AB=MN.
c) Tam giác ABC vuông tại A nên ABC^+C^=90∘
Suy ra: ABC^=90∘−C^=90∘−30∘=60∘
Suy ra: ABM^=12ABC^=12.60∘=30∘
Xét hai tam giác ABC và MAB, ta có:
BAC^=AMB^=90∘
ACB^=ABM^=30∘
Suy ra ∆ABC đồng dạng với ∆MAB (g.g)
Tỉ số đồng dạng: k=ABBC=510=12
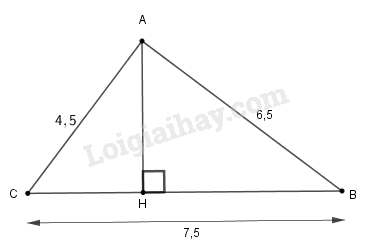
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B^,C^ và đường cao AH của tam giác.
b) Tìm tập hợp các điểm M sao cho SABC=SBMC.
Phương pháp giải:
a) Áp dụng định lí Pi-ta-go đảo và tỉ số lượng giác.
b) Dựa vào diện tích của các hình tam giác ABC và MBC để biện luận.
Lời giải:
a) Ta có:
AB2=62=36
AC2=4,52=20,25
BC2=7,52=56,25
Vì AB2+AC2=36+20,25=56,25=BC2 nên tam giác ABC vuông tại A ( theo định lí Pi-ta-go đảo).
Kẻ AH⊥BC. Xét tam giác ABC vuông tại A, theo hệ thức lượng trong tam giác vuông, ta có:
AH.BC=AB.AC⇔AH=AB.ACBC=6.4,57,5=3,6(cm)
Áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác ABC vuông, ta có: sinC^=ACBC=4,57,5=0,6
Suy ra: C^=53∘8′
Ta có:
B^+C^=90∘ (vì tam giác ABC vuông tại A)
⇒B^=90∘−C^=90∘−53∘8′=36∘52′
b) Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC=SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường x và y song song với BC cách BC một khoảng bằng AH.
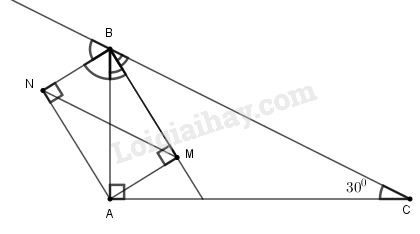
a) ∆ANL đồng dạng ∆ABC;
b) AN.BL.CM =AB.BC.CA.cosA.cosB.cosC.
Phương pháp giải:
Áp dụng kiến thức về hai tam giác đồng dạng và tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải:
a) Xét hai tam giác BNA và CLA, ta có:
BNA^=CLA^=90∘
A^ chung
Suy ra ∆BNA đồng dạng ∆CLA (g.g)
Suy ra: ALAN=ACAB⇒ALAC=ANAB
Xét hai tam giác ABC và ANL, ta có:
ALAC=ANAB
A^ chung
Suy ra ∆ABC đồng dạng ∆ANL (c.g.c)
b) ABN vuông tại N nên AN=AB.cosB^(1)
∆BCL vuông tại L nên BL=BC.cosB^(2)
∆ACM vuông tại M nên CM=AC.cosC^(3)
Từ (1), (2) và (3) suy ra:
AN.BL.CM=AB.BC.CA.cosA^cosB^cosC^.
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)