SBT Toán 9 Bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn | Giải SBT Toán lớp 9 

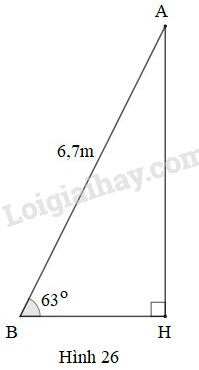
– Chiều cao của thang là cạnh góc vuông đối diện với góc .

– Tìm độ dài cạnh góc vuông ta lấy độ dài cạnh huyền nhân với sin góc đối diện.

Lời giải:

Xét tam giác AHB  vuông tại H, ta có:

AH=AB.sin⁡B^=6,7.sin⁡63∘ ≈6(m)

Vậy chiều cao của cái thang đạt được so với mặt đất là 6m.

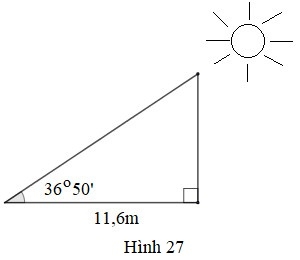
– Chiều cao của cột cờ là cạnh góc vuông đối diện với góc (36^circ 50′), bóng cột cờ là cạnh kề với góc nhọn.

– Tìm độ dài cạnh góc vuông ta lấy độ dài cạnh góc vuông kia nhân với tang góc đối.

– Chiều dài của dây kéo cờ gấp 2 lần chiều cao của cột cờ.

Lời giải:

Theo hệ thức giữa cạnh và đường cao trong tam giác vuông ta suy ra chiều cao cột cờ là :  11,6.tan⁡36∘50′≈8,69(m)

Chiều dài của dây kéo cờ là : 8,69.2=17,38(m)

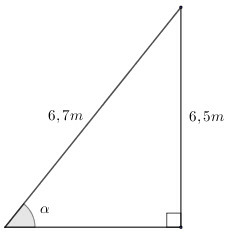
Một con mèo ở trên cành cây cao 6,5m. Để bắt mèo xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó, khi đó góc của thang với mặt đất là bao nhiêu, biết chiếc thang dài 6,7m ?

Phương pháp giải:

– Độ cao của con mèo chính là cạnh góc vuông đối diện với góc tạo bởi cái thang và mặt đất, chiều dài thang là cạnh huyền.

– Gọi α là góc tạo bởi cái thang và mặt đất, ta tìm sin⁡α bằng cách lấy 6,5 chia cho 6,7 (cạnh đối chia cạnh huyền), từ đó tìm được góc α. 

Lời giải:

Gọi α là góc tạo bởi cái thang và mặt đất.

Ta có: sin⁡α=6,56,7≈0,9701

Suy ra: α≈75∘57′

Vậy góc của thang so với mặt đất là 75∘57′.

Đài quan sát ở Toronto, Ontario, Canada cao 533m. Ở một thời điểm nào đó vào ban ngày, Mặt Trời chiếu tạo thành bóng dài 1100m. Hỏi lúc đó góc tạo bởi tia sáng mặt trời và mặt đất là bao nhiêu ? 

Phương pháp giải:

– Chiều cao của đài quan sát là cạnh góc vuông đối diện với góc nhọn, bóng của nó trên mặt đất là cạnh góc vuông kề với góc nhọn.

– Gọi α là góc tạo bởi  tia sáng mặt trời và mặt đất, ta tìm tgα bằng cách lấy 533 chia cho 1100, từ đó tìm được góc α. 

Lời giải:

Gọi α là góc tạo bởi  tia sáng mặt trời và mặt đất.

Ta có: tgα=5331100≈0,4845.

Suy ra: α≈25∘51′.

Vậy góc tạo bởi tia sáng mặt trời và mặt đất là 25∘51′

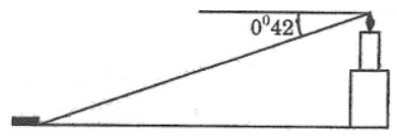
Một người quan sát ở đài hải đăng cao 80 feet (đơn vị đo lường Anh) so với mặt nước biển, nhìn một chiếc tàu ở xa với góc 0∘42′. Hỏi khoảng cách từ tàu đến chân hải đăng tính theo đơn vị hải lí là bao nhiêu? (1 hải lí = 5280 feet) (h.28). 

Phương pháp giải:

– Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc 0∘42′, khoảng cách từ tàu đến chân ngọn hải đăng là cạnh kề với góc nhọn. 

– Tìm độ dài cạnh góc vuông ta có thể lấy độ dài cạnh góc vuông kia nhân với côtang góc kề.

Lời giải:

Ta có : Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc 0∘42′, khoảng cách từ tàu đến chân ngọn hải đăng là cạnh kề với góc nhọn. 

Vậy khoảng cách từ tàu đến chân ngọn hải đăng là :

80.cot0∘42′≈6547,76 (feet) ≈1,24 (hải lí)

Một máy bay đang bay ở độ cao 10km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.

a) Nếu phi công muốn tạo góc nghiêng 3∘ thì cách sân bay bao nhiêu ki-lô-mét phải bắt đầu cho máy bay hạ cánh ?

b) Nếu cách sân bay 300km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu? 

Phương pháp giải:

– Độ cao của máy bay là cạnh góc vuông đối diện với góc nghiêng so với mặt đất. Khoảng cách từ máy bay đến sân bay là cạnh huyền. 

– Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền nhân với sin góc đổi, từ đó tìm cạnh huyền ta lấy cạnh góc vuông chia cho sin góc đổi.

– Gọi β là góc nghiêng của đường đi máy bay so với mặt đất. Tìm tìm sin⁡β bằng cách tìm tỉ số của 10km và 300km, từ đó tìm được góc β. 

Lời giải:

a) Ta có hình vẽ: Độ cao máy bay là AB=10km, góc nghiêng C^=30. Ta tính BC. 

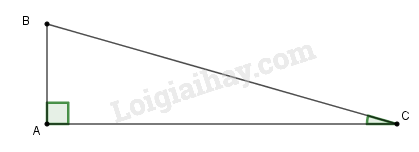
Vậy khoảng cách từ máy bay đến sân bay là:

BC=ABsin⁡C^=10sin⁡3∘≈191(km)

b) Ta có hình vẽ: Khi đó AB=10km,BC=300km 

Gọi C^=β là góc nghiêng của đường đi máy bay so với mặt đất. 

Ta có : sin⁡β=ABBC=10300=130.

Suy ra: β≈1∘55′.

Nếu cách sân bay 300km máy bay bắt đầu hạ cánh thì góc nghiêng là 1∘55′.

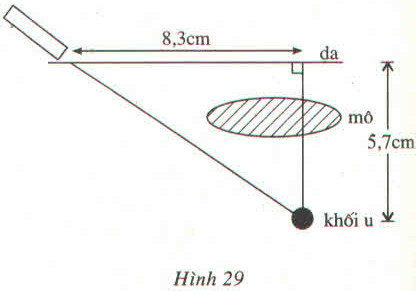
Một khối u của một căn bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) 8,3cm (h.29).

a) Hỏi góc tạo bởi chùm tia với mặt da?

b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?

Phương pháp giải:

– Khoảng cách từ mặt da đến khối u là cạnh góc vuông đối diện với góc nhọn, khoảng cách từ chùm tia đến mặt da là cạnh kề.

– Gọi β là góc tạo bởi chùm tia với mặt da. Tìm tìm tgβ bằng cách tìm tỉ số của 5,7cm và 8,3cm, từ đó tìm được góc β.

– Tìm độ dài từ chùm tia đến khối u ta lấy khoảng cách từ mặt da đến khối u chia cho sin⁡β.

Lời giải:

a) Khoảng cách từ mặt da đến khối u là cạnh góc vuông đối diện với góc nhọn, khoảng cách từ chùm tia đến mặt da là cạnh kề.

Gọi β là góc tạo bởi chùm tia với mặt da.

Ta có: tgβ=5,78,3≈0,6867.

Suy ra: β≈34∘29′.

Vậy góc tạo bởi chùm tia với mặt da là 34∘29′. 

b) Đoạn đường chùm tia đi đến khối u là:  

5,7sin⁡34∘29′≈10,07(cm).

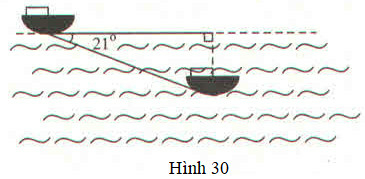
Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc 21∘ (h.30)

a) Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu?

b) Tàu phải chạy bao nhiêu mét để đạt đến độ sâu 1000m?

Phương pháp giải:

– Độ sâu của tàu là cạnh góc vuông đối diện với góc 21∘, đoạn đường đi của tàu là cạnh huyền, khoảng cách theo phương nằm ngang là cạnh kề của góc nhọn.

– Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc côsin góc kề.

Lời giải:

a) Độ sâu của tàu là cạnh góc vuông đối diện với góc 21∘, đoạn đường đi của tàu là cạnh huyền, khoảng cách theo phương nằm ngang là cạnh kề của góc nhọn.

Độ sâu của tàu đạt được là:     

300.sin⁡21∘≈107,5(m)

Khoảng cách từ tàu đến nơi xuất phát theo phương nằm ngang là:

300.cos⁡21∘≈280(m)

b) Đoạn đường tàu đi được là: 

1000sin⁡21∘≈2790(m)

Bài tập bổ sung (trang 119 SBT Toán 9)

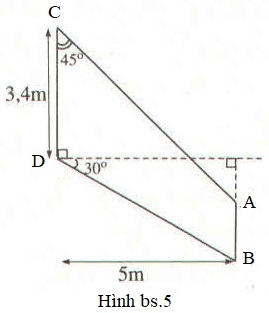
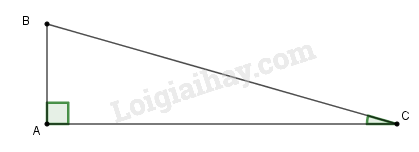
Áp dụng các hệ thức lượng trong tam giác vuông để tìm độ dài các cạnh AC,BD,AB.

Lời giải:

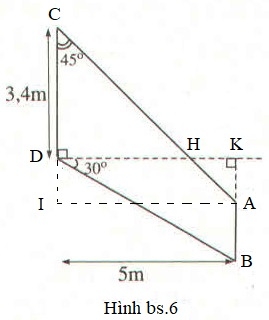
Đường thẳng AC cắt đường thẳng vuông góc với CD tại D ở điểm H thì tam giác CDH là tam giác vuông cân (vì là tam giác vuông có góc C bằng 450), DH=CD=3,4m.

Đường thẳng AB cắt DH tại K thì DK=5m nên H nằm ở giữa D và K (xem Hình bs.6).

Dựng hình chữ nhật AKDI thì AIC là tam giác vuông cân (vì là tam giác vuông có góc C bằng 450), AI=KD=5m

Xét tam giác vuông AIC ta có: AC=AI2+IC2=52+52=52(m)

Trong tam giác vuông BKD, có:

DB=DKcos⁡30∘=532=103 =1033≈5,77(m)

Vì DC//AK (cùng vuông với DK) nên KAH^=C^=450 (hai góc ở vị trí so le trong)

Suy ra HKA là tam giác vuông cân (tam giác vuông có góc A bằng 450)

Do đó: AK=HK=DK–DH=DK–DC =5–3,4=1,6m. 

Xét tam giác vuông BDK, ta có: KB=DK.tg30∘ =5.33 =533.  

Suy ra : AB=KB–KA =533−1,6≈1,29(m).