tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
Ta sử dụng kiến thức:
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải:
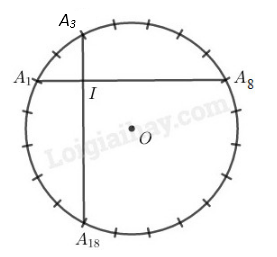
Đường tròn (O) được chia thành 20 cung bằng nhau nên số đo mỗi cung bằng
360o:20=18o
Gọi giao điểm của A1A8 và A3A16 là I.
Ta có: sđA1A3⏜ =2.180=36o
sđA8A16⏜ =8.180=144o
Ta có: A1IA3^=12(sđA1A3⏜+sđA8A16⏜) (góc có đỉnh ở trong đường tròn (O))
⇒ A1IA3^=36∘+144∘2=90∘
⇒A1A8⊥A3A16
Ta sử dụng kiến thức:
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Số đo của nửa đường tròn bằng 180o.
+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải:
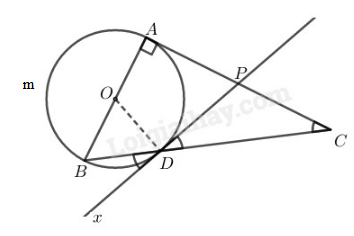
Trong đường tròn (O) ta có C^ là góc có đỉnh ở ngoài đường tròn.
C^=12(sđAmB⏜ – sđ AD⏜) (tính chất góc có đỉnh ở ngoài đường tròn)
mà sđAmB⏜=sđADB⏜=180o
C^=12(sđADB⏜ – sđ AD⏜) =12(sđAD⏜ + sđ DB⏜ – sđ AD⏜)=12sđBD⏜ (1)
CDP^=BDx^ (đối đỉnh) (2)
BDx^=12sđBD⏜ (góc giữa tia tiếp tuyến và dây cung) (3)
Từ (1), (2) và (3) suy ra: C^=CDP^⇒ΔPCD cân tại P.
Vậy PD=PC
Ta sử dụng kiến thức:
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Tính chất góc ngoài của tam giác: Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
Lời giải:
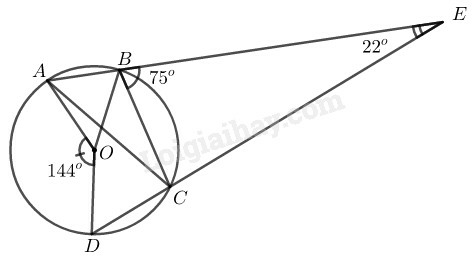
Trong đường tròn (O) ta có E^ là góc có đỉnh ở ngoài đường tròn.
E^=12(sđAD⏜−sđBC⏜)
Lại có: sđAD⏜=AOD^=144∘
⇒22∘=144∘−sđBC⏜2
⇒sđBC⏜=144∘−2.22∘=100∘
Ta có: BAC^=12sđBC⏜ (tính chất góc nội tiếp)
⇒ BAC^=12.100∘=50∘
Trong ∆ABC ta có CBE^ là góc ngoài tại đỉnh B.
⇒ CBE^=BAC^+ACB^ (tính chất góc ngoài của tam giác)
⇒ ACB^=CBE^−BAC^=75∘−50∘=25∘
ACB^=12AOB^ (hệ quả góc nội tiếp)
AOB^=2.ACB^=50∘
Vậy AOB^=BAC^=50∘
+) Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Trong tam giác cân, đường phân giác ứng với góc ở đỉnh cũng là đường cao.
Lời giải:
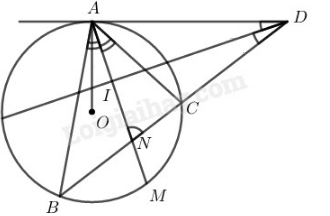
Ta có: BAM^=MAC^ (vì AM là tia phân giác của BAC^)
⇒BM⏜= CM⏜ (1)
Ta có: DAM^=12sđACM⏜ (góc giữa tia tiếp tuyến và dây cung)
Hay DAM^=12(sđAC⏜+sđCM⏜ )(2)
Gọi N là giao điểm của AM và BC.
Ta có: ANC^ là góc có đỉnh ở trong đường tròn (O).
⇒ ANC^=12(sđAC⏜+sđBM⏜)(3)
Từ (1), (2) và (3) suy ra: DAM^=ANC^ hay DAN^=AND^
Suy ra: ∆DAN cân tại D có DI là tia phân giác nên suy ra DI là đường cao
⇒ DI⊥AN hay DI⊥AM
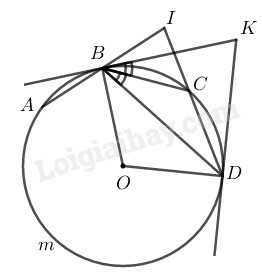
a) Chứng minh BIC^=BKD^
b) Chứng minh BC là tia phân giác của KBD^.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.
+) Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Lời giải:
a) AB⏜=BC⏜=CD⏜ (gt) (1)
Trong đường tròn (O) ta có BKD^ là góc có đỉnh ở ngoài đường tròn.
⇒BKD^=12(sđBAD⏜−sđBCD⏜)
=12(sđAB⏜+sđAmD⏜−sđBC⏜−sđCD⏜) (2)
Từ (1) và (2) ⇒BKD^=12(sđAmD⏜−sđBC⏜)(3)
Trong đường tròn (O) ta có BIC^ là góc có đỉnh ở ngoài đường tròn.
⇒BIC^=12 (sđ AmD⏜ – sđ BC⏜) (4)
Từ (3) và (4) suy ra: BIC^=BKD^
b) Xét đường tròn (O) ta có:
+) KBC^=12sđ BC⏜ (tính chất góc tạo bởi tia tiếp tuyến và dây cung) (5)
+) CBD^=12sđCD⏜ (tính chất góc nội tiếp) (6)
Từ (1), (5) và (6) suy ra: KBC^=CBD^. Vậy BC là tia phân giác của KBD^.
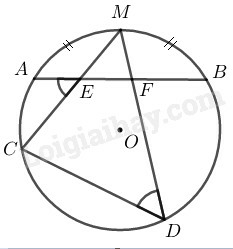
Bài tập bổ sung (trang 105 SBT Toán 9)
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Tổng các góc trong một tứ giác bằng 360o.
Lời giải:
Ta có M là điểm chính giữa cung nhỏ AB⏜
⇒sđMA⏜=sđMB⏜ (1)
Lại có: D^=12sđMAC⏜ (tính chất góc nội tiếp)
⇒ D^=12(sđMA⏜+sđAC⏜) (2)
Và AEC^=12 (sđ MB⏜ + sđ AC⏜) (tính chất góc có đỉnh ở trong đường tròn) (3)
Từ (1), (2) và (3) suy ra: D^=AEC^
AEC^+CEF^=180∘ (kề bù)
⇒D^+CEF^=180o (4)
Trong tứ giác CEFD ta có:
CEF^+D^+ECD^+EFD^=360o (tổng các góc trong tứ giác) (5)
Từ (4) và (5) suy ra: ECD^+EFD^=180o
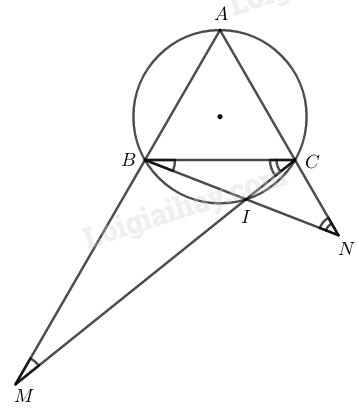
a) ANB^=BCI^
b) AMC^=CBI^
Phương pháp giải:
Ta sử dụng kiến thức:
+) Với hai cung nhỏ trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu C là một điểm trên cung AB thì sđAB⏜=sđAC⏜+sđCB⏜.
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Lời giải:
Vì AB=AC=BC(gt)
Suy ra các cung nhỏ AB⏜=AC⏜=BC⏜ (1)
a) Xét đường tròn (O) có: BCI^=12sđBI⏜ (tính chất góc nội tiếp)
hay BCI^=12(sđBC⏜−sđCI⏜) (2)
Từ (1) và (2) suy ra: BCI^=12(sđAB⏜−sđCI⏜) (3)
Lại có: ANB^=12(sđAB⏜−sđCI⏜) (góc có ở đỉnh bên ngoài đường tròn) (4)
Từ (3) và (4) suy ra: ANB^=BCI^
b) Xét đường tròn (O) có: CBI^=12sđCI⏜ (tính chất góc nội tiếp)
Hay CBI^=12(sđBC⏜−sđBI⏜) (5)
Từ (1) và (5) suy ra: CBI^=12(sđAC⏜−sđBI⏜) (6)
Lại có: AMC^=12(sđAC⏜−sđBI⏜) (góc có đỉnh bên ngoài đường tròn) (7)
Từ (6) và (7) suy ra: AMC^=CBI^.
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)