tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu
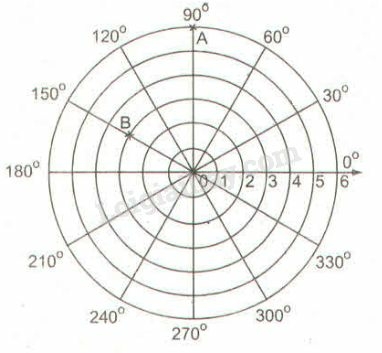
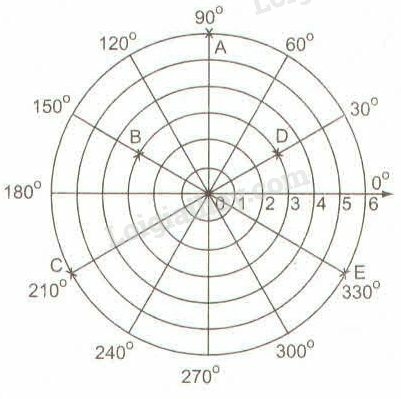
a) Trong hình 102, cho A là giao điểm của đường tròn (0;6) với tia 90o và kí hiệu là A(6;90o). Tương tự B là giao điểm của đường tròn (0;3) với tia 150o và kí hiệu là B(3;150o). Hãy đánh dấu các điểm C(6;210o),D(3;30o) và E(6;330o) trên hình 102.
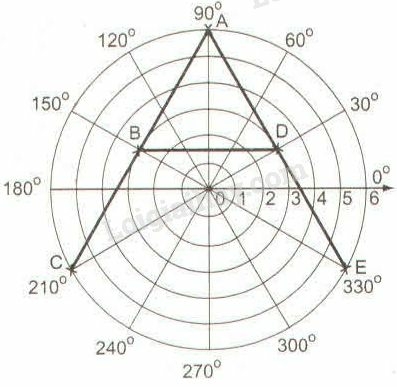
b) Nối AB,BC,AD,DE và BD em thấy hình gì?
Phương pháp giải:
Quan sát hình vẽ để tìm các giao điểm.
Lời giải:
a) Ta đánh dấu các điểm như sau:
b)
Nối AB,BC,AD,DE và BD ta thu được hình chữ A.
(A) x(cm); (B) 2x(cm)
(C) x2(cm) (D) 2x(cm)
Phương pháp giải:
Sử dụng: Trong một tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải:
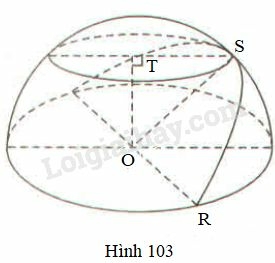
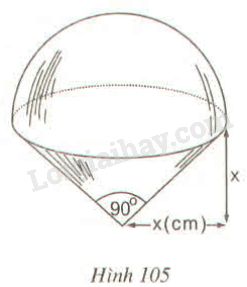
Ta có OS=OR=x (= bán kính)
ΔSTO vuông tại T có TOS^=45o
Ta có ST=OS.sin45o=x.22=x2 (cm).
Chọn (C).
(A) Hình tròn có bán kính 2cm.
(B) Hình vuông có độ dài cạnh 3,5cm.
(C) Tam giác với độ dài các cạnh là 3cm,4cm,5cm.
(D) Nửa mặt cầu bán kính 4cm.
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Diện tích hình tròn bán kính r là: S=πr2.
– Diện tích hình vuông cạnh a là S=a2.
– Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.
– Diện tích mặt cầu bán kính r là: S=4πr2.
Lời giải:
(A) Hình tròn có bán kính 2cm có diện tích là: S=πr2=π.22=4π(cm2)
(B) Hình vuông có cạnh bằng 3,5cm có diện tích là: S=a2=3,52=12,25(cm2)
(C) Ta có: 32+42=52 do đó tam giác có độ dài các cạnh 3cm,4cm,5cm là tam giác vuông.
Diện tích tam giác đó là:
S=12.3.4=6(cm2)
(D) Diện tích nửa mặt cầu bán kính 4cm là:
S=12.4πr2=12.4π.42=32π(cm2).
Vậy trong các hình trên thì nửa mặt cầu bán kính 4cm có diện tích lớn nhất
Chọn D.
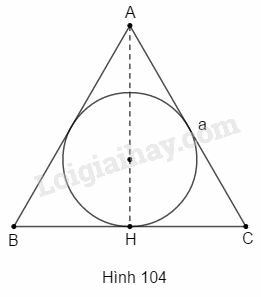
Cho hình quay một vòng xung quanh đường cao AH của tam giác đó, (xem hình 104), ta được một hình nón ngoại tiếp hình cầu. Tính thể tích phần hình nón bên ngoài hình cầu.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón có bán kính đáy r, chiều cao h là: V=13πr2h.
– Thể tích hình cầu bán kính r là: V=43πr3.
Lời giải:
Gọi h là đường cao của tam giác đều, r là bán kính của đường tròn nội tiếp tam giác đó.
Trong ΔAHC có AHC^=90o;C^=60o.
AH=AC.sinC=a.sin600=a32
ΔABC đều, tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác đồng thời là giao ba đường trung tuyến, giao ba đường trung trực nên ta có O là trọng tâm tam giác ABC
r=OH=13AH=a36
Thể tích hình nón là:
V1=13π.BH2.AH=13π(a2)2.a32=πa3324 (đơn vị thể tích)
Thể tích hình cầu là:
V2=43πr3=43π.(a36)3=43π.3a33216=πa3354 (đơn vị thể tích).
Phần thể tích hình nón nằm ngoài hình cầu là:
V=V1−V2=πa3324−πa3354=9πa33−4πa33216=5πa33216 (đơn vị thể tích)
Tỉ số các thể tích của 2 hình cầu này là:
(A) 1:2 (B) 1:4 (C) 1:8
(D) Một kết quả khác.
Hãy chọn kết quả đúng.
Phương pháp giải:
Áp dụng công thức:
Thể tích hình cầu bán kính R : V=43πR3.
Lời giải:
Hình cầu A có bán kính r=x có thể tích là: V1=43πx3(cm3)
Hình cầu B có bán kính r=2x có thể tích là: V2=43π(2x)3=323πx3(cm3)
V1:V2=43:323=43.332=18
Chọn (C).
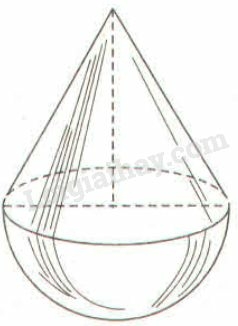
Thể tích của hình nhận giá trị nào trong các giá trị sau:
(A) 23πx3(cm3) (B) πx3(cm3)
(C) 43πx3(cm3) (D) 2πx3(cm3)
Phương pháp giải:
Sử dụng:
– Thể tích hình nón có bán kính đáy r, chiều cao h là: V=13πr2h.
– Thể tích hình cầu bán kính r là: V=43πr3.
Lời giải:
Hình gồm một nửa hình cầu có bán kính là x và một hình nón có bán kính đáy bằng x, chiều cao bằng x.
Thể tích nửa hình cầu là: V1=12.43πx3=23πx3(cm3)
Thể tích của hình nón là: V2=13π.x2.x=13πx3(cm3)
Tổng thể tích của hai hình đó là: V=23πx3+13πx3=πx3(cm3)
Chọn (B).
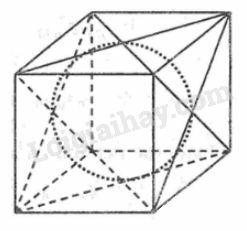
a) Tính tỉ số giữa diện tích toàn phần của hình lập phương với diện tích mặt cầu
b) Nếu diện tích mặt cầu là 7π(cm2) thì diện tích toàn phần của hình lập phương là bao nhiêu?
c) Nếu bán kính hình cầu là 4cm thì thể tích phần trống (trong hình hộp ngoài hình cầu) là bao nhiêu?
Phương pháp giải:
Sử dụng:
– Diện tích toàn phần của hình lập phương cạnh a là: S=6a2.
– Diện tích mặt cầu bán kính r là: S=4πr2.
– Thể tích hình lập phương cạnh a là: V=a3.
– Thể tích hình cầu bán kính r là: V=43πr3.
Lời giải:
Gọi cạnh hình lập phương là a thì bán kính cầu r=a2.
a) Diện tích toàn phần của hình lập phương là: S1=6a2 (đơn vị diện tích)
Diện tích mặt cầu là: S2=4.π.(a2)2=4π.a24=πa2 (đơn vị diện tích)
Tỉ số S1S2=6a2πa2=6π
b) Theo câu a ta có S1S2=6π
Diện tích mặt cầu bằng 7π(cm2) nên ta có S17π=6π
⇒S1=6π.7π=42 (cm2)
Vậy diện tích mặt cầu là 7π(cm2) thì diện tích toàn phần của hình lập phương là 42 (cm2).
c) Bán kính hình cầu r=4cm thì cạnh hình lập phương a=2r=8cm.
Thể tích của hình lập phương là: V1=a3=83=512(cm3)
Thể tích hình cầu là: V2=43πr3=43π.43=2563π(cm3)
Thể tích hình lập phương nằm ngoài hình cầu là:
V=V1−V2=512−2563π≈243,917(cm3)
Một đồ chơi “lắc lư” của trẻ em gồm một hình nón gắn với nửa hình cầu (h.107) (chiều cao của hình nón bằng đường kính đường tròn đáy). Có hai loại đồ chơi: loại thứ nhất cao 9cm, loại thứ hai cao 18cm.
a) Tỉ số: thể tích đồ chơi loại thứ haithể tích đồ chơi loại thứ nhất
(A) 2 (C) 8
(B) 4 (D) 16
Hãy chọn kết quả đúng.
b) Trong các số sau đây:
(A) 2(cm) (C) 4(cm)
(B) 3(cm) (D) 412(cm)
Số nào là bán kính đường tròn đáy của đồ chơi loại thứ nhất?
c) Trong các số sau đây:
(A) 30π(cm3) (B) 36π(cm3)
(C) 72π(cm3) (D) 610(cm3)
Số nào là thể tích của loại đồ chơi thứ nhất?
Phương pháp giải:
Sử dụng:
– Thể tích hình nón có bán kính đáy r, chiều cao h là: V=13πr2h.
– Thể tích hình cầu bán kính r là: V=43πr3.
Lời giải:
a) Loại thứ nhất có chiều cao 9cm là bao gồm chiều cao của hình nón và bán kính của hình cầu, mà chiều cao hình nón bằng đường kính hình cầu.
Gọi r là bán kính của hình cầu ta có:
2r+r=9⇒r=3(cm)
Chiều cao hình nón là: h=2r=6cm
Thể tích hình nón là: V1=13πr2.h=13π.32.6=18π (cm3)
Thể tích nửa hình cầu là: V2=12.43π.33=18π(cm3)
Thể tích loại đồ chơi thứ nhất là: 18π+18π=36π(cm3)
Loại thứ 2 có chiều cao 18cm là bao gồm chiều cao hình nón và bán kính hình cầu mà chiều cao hình nón bằng đường kính hình cầu.
Gọi R là bán kính của hình cầu ta có:
2R+R=18⇒R=6cm
Chiều cao hình nón là: h′=2R=12cm
Thể tích hình nón là: V1′=13πR2.h′=13π.62.12=144π (cm3)
Thể tích nửa hình cầu là: V2′=12.43πR3=12.43π.63=144π (cm3)
Thể tích loại đồ chơi thứ 2 là: 144π+144π=288π(cm3)
thể tích đồ chơi loại thứ haithể tích đồ chơi loại thứ nhất =288π36π=8
Chọn (C).
b) Bán kính đường tròn đáy đồ chơi thứ nhất là r=3cm.
Chọn (B).
c) Thể tích loại đồ chơi thứ nhất là: 18π+18π=36π(cm3).
Chọn (B).
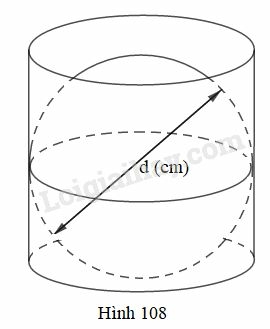
Nếu đường kính của hình cầu là d(cm) thì thể tích của hình trụ là:
(A) 14πd3(cm3) (B) 13πd3(cm3)
(C) 23πd3(cm3) (D) 34πd3(cm3)
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng: Thể tích hình trụ có bán kính đáy r, chiều cao h là: V=πr2h.
Lời giải:
Ta có bán kính hình cầu bằng bán kính đáy hình trụ, chiều cao hình trụ bằng đường kính hình cầu.
Do đó, khi đường kính hình cầu là d(cm) thì bán kính đáy hình trụ là d2(cm) và chiều cao hình trụ là d (cm).
Thể tích hình trụ là: V=πr2.h=π.(d2)2.d=14πd3 (cm3)
Chọn (A).
Với hai quả dưa hấu (xem như là 2 hình cầu) một to và một nhỏ, tỉ số các đường kính của chúng là 5:4, nhưng giá của quả to gấp rưỡi giá của quả nhỏ. Bạn chọn mua quả nào lợi hơn? (xem “chất lượng” của chúng là như nhau).
Phương pháp giải:
Sử dụng: Thể tích hình cầu bán kính r là: V=43πr3.
Lời giải:
Gọi bán kính quả nhỏ là r thì bán kính quả lớn là 54r.
Thể tích quả nhỏ là: V=43πr3;
Thể tích quả to là: V=43π(54r)3
Tỉ số 2 thể tích là: 43πr3(54)3:43πr3=(54)3=12564
Mua quả to lợi hơn vì thể tích gần gấp đôi mà giá tiền chỉ gấp rưỡi.
(A) 1 (C) 3
(B) 2 (D) 4
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón có bán kính đáy r, chiều cao h là: V=13πr2h.
– Thể tích hình trụ có bán kính đáy r, chiều cao h là: V=πr2h.
Lời giải:
Giả sử hình trụ và hình nón có cùng bán kính r và chiều cao h.
Thể tích hình trụ là: V=πr2.h
Thể tích hình nón là: V′=13πr2.h
⇒V=3V′.
Vậy phải múc 3 lần.
Chọn (C).
Như vậy diện tích toàn bộ của khối gỗ là:
(A) 4πr2(cm2) (B) 6πr2(cm2)
(C) 8πr2(cm2) (D) 10πr2(cm2)
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Diện tích xung quanh hình trụ là: Sxq=2πrh.
(r là bán kính đáy, h là chiều cao).
– Diện tích mặt cầu bán kính r là: S=4πr2.
Lời giải:
Diện tích toàn bộ khối gỗ bằng diện tích xung quanh hình trụ cộng với diện tích hai nửa mặt cầu
Diện tích xung quanh hình trụ là: Sxq=2πr.h=2πr.2r=4πr2(cm2)
Diện tích hai nửa mặt cầu là: S=2.2πr2=4πr2(cm2)
Diện tích toàn bộ khối gỗ là: 4πr2+4πr2=8πr2(cm2).
Chọn (C).
Phương pháp giải:
Sử dụng:
– Độ dài đường tròn lớn của hình cầu bán kính r là C=2πr.
– Thể tích hình cầu bán kính r là V=43πr3.
Lời giải:
Dùng thước dây tạo ra đường tròn đặt vừa khít hình cầu, ta có độ dài của đường tròn lớn là C.
Bán kính của hình cầu là: r=C2π.
Thể tích hình cầu là: V=43π.(C2π)3=43π.C38π3=C36π2.
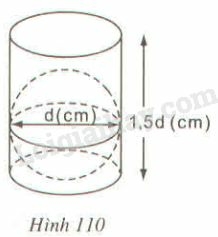
Tỉ số của thể tích hình trụ này và thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ là:
(A) 43 (C) 31
(B) 94 (D) 49
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Thể tích hình trụ có bán kính đáy r, chiều cao h là: V=πr2h.
– Thể tích hình cầu bán kính r là: V=43πr3.
Lời giải:
Vì chiều cao của một hình trụ gấp ba lần bán kính đáy của nó nên nếu bán kính đáy hình trụ là r thì chiều cao hình trụ là h=3r
Thể tích của hình trụ là: V1=πr2.h=πr2.3r=3πr3
Thể tích của hình cầu là: V2=43πr3
Ta có V1V2=94
Chọn (B).
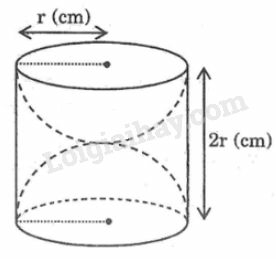
(A) 23 (C) 29
(B) 49 (D) 13
Đâu là tỉ số VcầuVtrụ?
Phương pháp giải:
Sử dụng:
– Thể tích hình trụ có bán kính đáy r, chiều cao h là: V=πr2h.
– Thể tích hình cầu bán kính r là: V=43πr3.
Lời giải:
Gọi r là bán kính đường tròn đáy hình trụ thì r cũng là bán kính hình cầu.
Suy ra d=2r
Chiều cao hình trụ là: h=1,5d=32d=32.2r=3r
Thể tích của hình trụ là: V1=πr2.h=πr2.3r=3πr3
Thể tích của hình cầu là: V2=43πr3
Ta có: V2V1=43πr33πr3=49.
Chọn (B).
