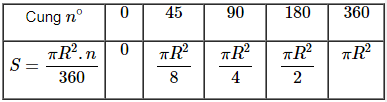tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 10: Diện tích hình tròn, hình quạt tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 10: Diện tích hình tròn, hình quạt tròn
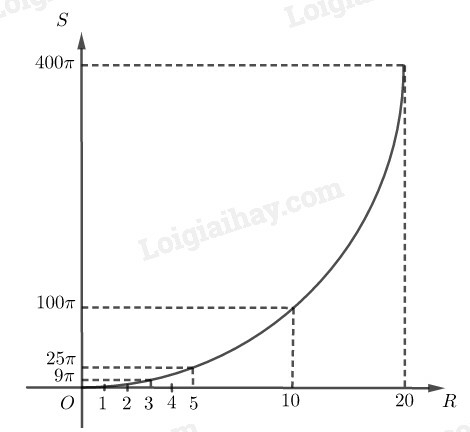
a) Điền vào ô trống trong bảng sau (S là diện tích hình tròn bán kính R).
|
R |
0 |
1 |
2 |
3 |
4 |
5 |
10 |
20 |
|
S |
|
|
|
|
|
|
|
|
b) Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó.
c) Diện tích hình tròn có tỉ lệ thuận với bán kính không?
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR
Lời giải:
a)
b) Vẽ đồ thị:
c) Diện tích hình tròn không tỉ lệ thuận với bán kính
a) Điền vào ô trống trong bảng sau (S là diện tích hình quạt n∘).
|
Cung n∘ |
0 |
45 |
90 |
180 |
360 |
|
S |
|
|
|
|
|
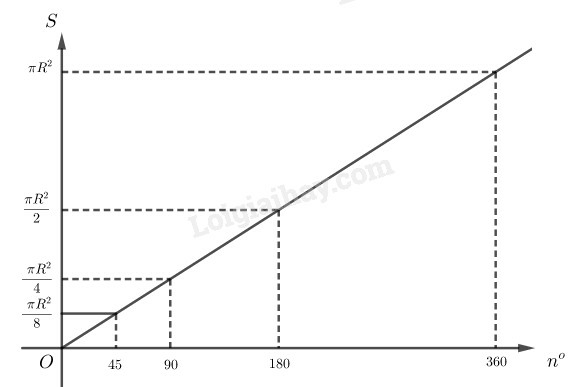
b) Vẽ đồ thị biểu diễn diện tích hình quạt theo n∘.
c) Diện tích hình quạt có tỉ lệ thuận với số đo độ của cung không?
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích hình quạt tròn bán kính R, cung n∘ được tính theo công thức: S=πR2n360 hay S=lR2
Lời giải:
a)
b) Vẽ đồ thị:
c) Diện tích hình quạt tròn tỉ lệ thuận với số đo độ của cung tròn.
Ta sử dụng kiến thức:
+) Độ dài C của một đường tròn bán kính R được tính theo công thức: C=2πR
+) Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2
Lời giải:
Gọi bán kính của hình tròn là R, diện tích là S.
Ta có: C=2πR
⇒R=C2π
S=πR2=π.(C2π)2
=π.C24π2=C24π (đơn vị diện tích)
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2
Lời giải:
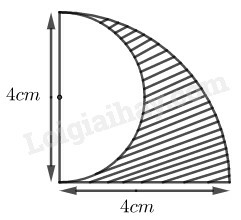
Hình để trắng là nửa hình tròn có đường kính 4cm nên bán kính bằng 2cm có diện tích:
S1=12π.22=2π (cm2)
Diện tích 14 hình tròn có bán kính 4cm:
S=14π.42=4π (cm2)
Diện tích phần gạch sọc:
S2=S−S1=4π−2π=2π (cm2)
Vậy:S1=S2
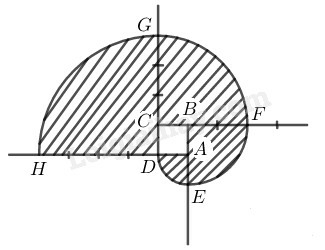
a) Vẽ đường xoắn (h.11) xuất phát từ một hình vuông cạnh 1cm. Nói cách vẽ.
b) Tính diện tích hình gạch sọc.
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2
Lời giải:
a)
– Vẽ hình vuông ABCD có cạnh 1cm
– Vẽ cung đường tròn tâm A bán kính 1cm ta được cung DE⏜
– Vẽ cung đường tròn tâm B bán kính 2cm ta được cung EF⏜
– Vẽ cung đường tròn tâm C bán kính 3cm ta được cung FG⏜
– Vẽ cung đường tròn tâm D bán kính 4cm ta được cung GH⏜
b) Tính diện tích phần gạch sọc.
Diện tích hình quạt DAE=14π.12
Diện tích hình quạt EBF=14π.22
Diện tích hình quạt FCG=14π.32
Diện tích hình quạt GDH=14π.42
Diện tích phần gạch sọc:
S=14π(12+22+32+42)=152(cm2)
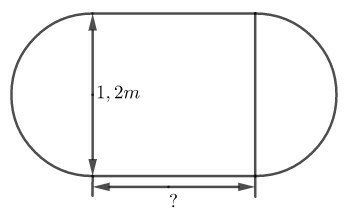
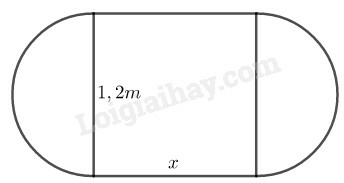
a) Kích thước kia của hình chữ nhật phải là bao nhiều nếu diện tích mặt bàn tăng gấp đôi sau khi nới?
b) Kích thước kia của hình chữ nhật phải là bao nhiêu nếu chu vi mặt bàn tăng gấp đôi sau khi nới?
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2
Lời giải:
a) Gọi kích thước thứ 2 của hình chữ nhật là x(cm), điều kiện: x>0
Ta có: 1,2.x+π(0,6)2=2.π(0,6)2
⇒1,2.x=π.(0,6)2
x=π.0,362≈0,942 (m)
b) Gọi kích thước thứ 2 của hình chữ nhật là x(cm), điều kiện: x>0
Chu vi mặt bàn mới là 1,2.π+2x
Theo bài ra ta có: 1,2π.2x=2.1,2π
⇒x=1,2π2≈1,885 (m)
Ta sử dụng kiến thức:
+) Áp dụng tính chất dãy tỉ số bằng nhau: Từ dãy tỉ số bằng nhau ab=cd=ef ta suy ra: ab=cd=ef=a+c+eb+d+f.
+) Diện tích hình quạt tròn bán kính R, cung n∘ được tính theo công thức: S=πR2n360.
Lời giải:
Gọi số đo độ của 3 cung theo thứ tự là a,b,c (0<a,b,c<360)
Ta có a+b+c=360∘
Theo bài ra ta có:
a3=b4=c5=a+b+c3+4+5=360∘12=30∘
a=3.30∘=90∘;
b=4.30∘=120∘;
c=5.30∘=150∘
Diện tích các hình quạt tương ứng với cung 90∘,120∘,150∘ là S1,S2,S3
S1=πR2.90360=πR24
S2=πR2.120360=πR23
S3=πR2.150360=5πR212
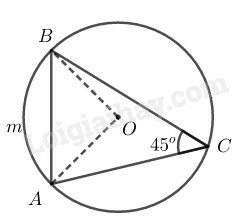
a) Tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
b) Tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích hình quạt tròn bán kính R, cung n∘ được tính theo công thức: S=πR2n360.
Lời giải:
a) Xét đường tròn (O) có C^=45∘ (gt) là g
óc nội tiếp chắn AmB⏜
⇒sđAmB⏜=2.C^=2.450=90∘
Diện tích hình quạt AOB là:
S=πR2.90360=πR24 (đơn vị diện tích)
b) AOB^=sđAmB⏜=900
⇒OA⊥OB
Diện tích tam giác OAB là: S=12OA.OB=R22
Diện tích hình viên phân AmB là:
SqAOB−SAOB=πR24−R22=R2(π−2)4 (đơn vị diện tích)
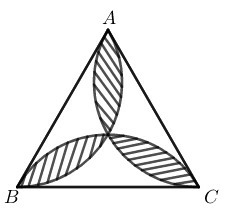
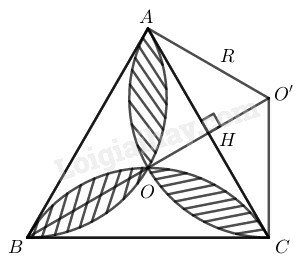
Phương pháp giải:
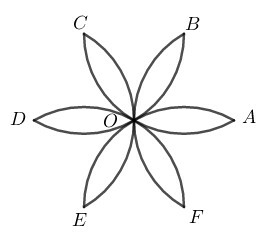
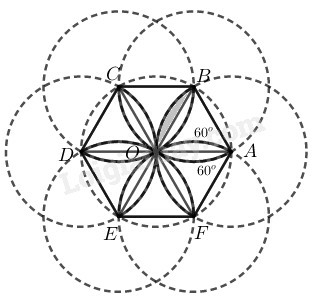
Ta sử dụng kiến thức:
+) Diện tích hình quạt tròn bán kính R, cung n∘ được tính theo công thức: S=πR2n360.
Lời giải:
Diện tích hình hoa thị bằng tổng diện tích 3 hình viên phân trừ diện tích tam giác đều ABC.
Gọi O là tâm của tam giác đều ABC
⇒OA=OB=OC
Vì ∆ABC đều nên AO, BO, CO là phân giác của các góc A^,B^,C^
OAC^=OCA^=60∘2=30∘
AOC^=180∘−(30∘+30∘)=120∘
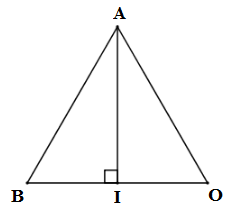
Trong tam giác O′HA có O′HA^=90∘, HO′A^=60∘
AH=R.sinHO′A^=R.sin60∘=R32
AC=2AH=R3
⇒R=AC3=a3=a33
Squạt=π(a33)2.120360
=πa233=πa29 (đơn vị diện tích)
∆O′HA có O′HA^=90∘; HO′A^=60∘
O′A=R.cos60∘=a33.12=a36
SΔO′CA=12O′H.AC=12.a36.a=a2312 (đơn vị diện tích)
Diện tích hình viên phân:
Svp=Squạt−SΔO′CA =πa29−a2312=4πa2−3a2336
Diện tích tam giác đều ABC cạnh a: SABC=a234 (đơn vị diện tích)
Diện tích hình hoa thị là:
S=3Svp−SABC=3.4πR2−3a2336−a234
=4πa2−3a2312−3a2312
=4πa2−6a2312=a26(2π−33) (đơn vị diện tích)
a) Diện tích hình tròn (O).
b) Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ).
c) Diện tích hình quạt tròn AOH (ứng với cung nhỏ AH).
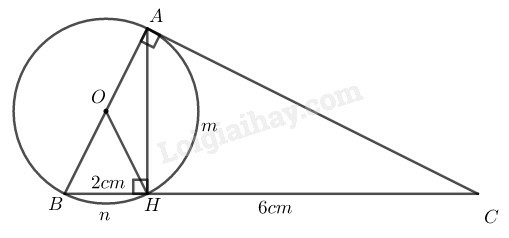
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương một cạnh góc vuông bằng tích cạnh huyền với hình chiếu của cạnh góc vuông đó trên cạnh huyền.
+) Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải:
a) ∆ABC có A^=900
Theo hệ thức lượng trong tam giác vuông ta có:
AB2=BH.BC⇒AB2=2.(2+6)=16
Suy ra AB=4(cm)
Diện tích hình tròn tâm O là:
S=π(AB2)2=π(42)2=4π (cm2)
b) Trong tam giác vuông ABC ta có:
AH2=HB.HC=2.6=12
Suy ra AH=23 (cm)
SΔAHB=12AH.BH=12.2.23=23 (cm2)
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O trừ diện tích ∆AHB nên tổng diện tích hai hình viên phân là:
S=2π−23=2(π−3) (cm2)
c) ∆BOH có OB=OH=BH=2cm
⇒ΔBOH đều
⇒B^=600
B^=12sđAmH⏜ (tính chất góc nội tiếp)
⇒sđAmH⏜ =2B^=1200
SqAOH=π.22.120360=4π3 (cm2)
Bài tập bổ sung (trang 113 SBT Toán 9)
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2
Lời giải:
Hình đó gồm nửa hình tròn bán kính 5R, 3 nửa hình tròn bán kính R và bớt đi 2 nửa hình tròn bán kính R.
S=π(5R)22+3.πR22−2.πR22
=25R2π2+πR22
=26πR22=13πR2 (đơn vị diện tích)
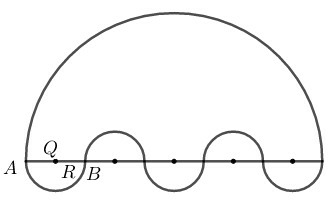
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong đường tròn R, độ dài l của một cung n∘ được tính theo công thức: l=πRn180.
+) Diện tích hình quạt tròn bán kính R, cung n∘ được tính theo công thức: S=πR2n360 hay S=lR2
Lời giải:
Ta có 12 hình viên phân có diện tích bằng nhau tạo nên cánh hoa đó.
Xét hình viên phân giới hạn bởi cung BO⏜ và dây căng cung đó thì cung BO⏜ là cung của đường tròn tâm A bán kính R.
OA=AB=OB=R
⇒ΔAOB đều ⇒OAB^=600
Diện tích hình quạt AOB là:
S′=πR2.60360=πR26
Kẻ AI⊥BO tại I.
Trong tam giác vuông AIO ta có:
AI=AO.sinAOI^=R.sin600=R32
SΔAOB=12AI.AB=12.R32.R=R234
Diện tích 1 hình viên phân là:
S1=S′−SΔAOB
=πR26−R234=2πR2−3R2312
Diện tích của hình cánh hoa:
S=12.S1=12.2πR2−3R2312=R2(2π−33) (đơn vị diện tích)
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)