tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
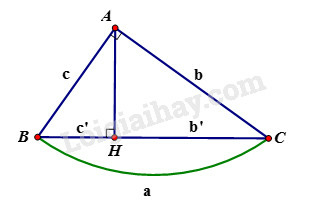
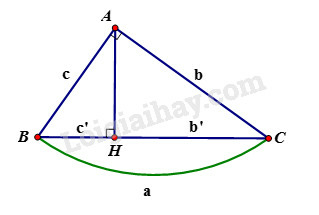
Phương pháp giải:
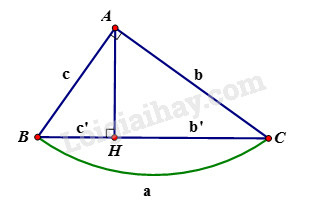
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+)AC2=CH.BC hay b2=ab′
+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)
Lời giải:
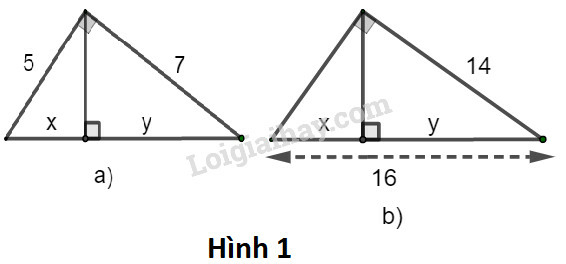
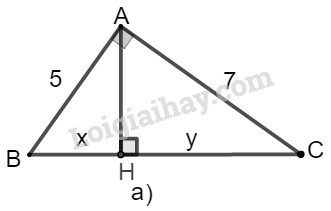
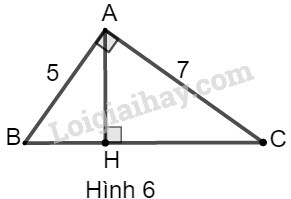
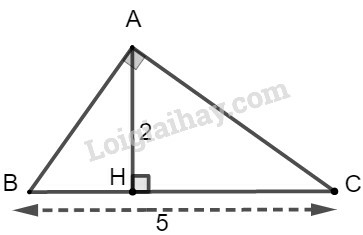
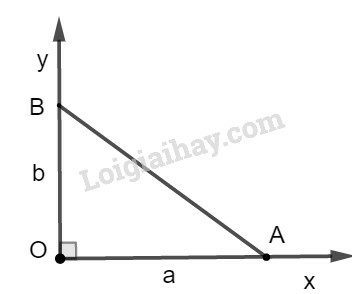
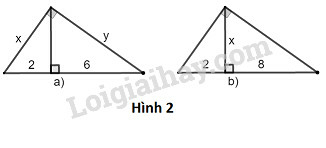
a) Ta đặt tên như hình vẽ dưới đây:
Xét tam giác ABC có chiều cao AH.
Theo định lý Py-ta-go, ta có:
BC2=AC2+AB2=52+72
Hay x+y=BC=52+72=74
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
AB2=BH.BC
⇒52=x.74⇒x=2574
Thay x=2574 vào x+y=74, ta có:
y+2574=74⇒y=74−2574=74−2574=4974
Vậy x=2574;y=4974.
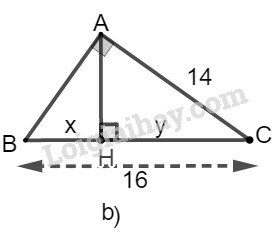
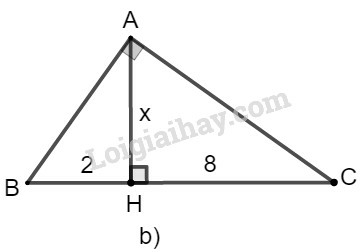
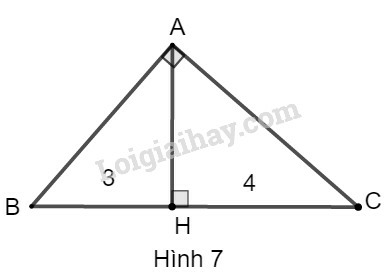
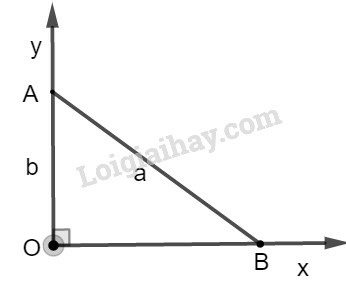
b) Ta đặt tên như hình vẽ dưới đây:
Xét tam giác ABC có chiều cao AH.
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AC2=CH.BC
⇒142=y.16⇒y=14216=19616=12,25
Mà x+y=16⇒x=16−y=16−12,25=3,75
Vậy x=12,25;y=3,75.
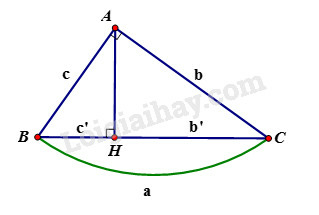
Phương pháp giải:
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+) AC2=CH.BC hay b2=ab′
+) AH=HB.HC hay h=c′.b′
Lời giải:
a) Đặt tên hình như hình dưới đây:
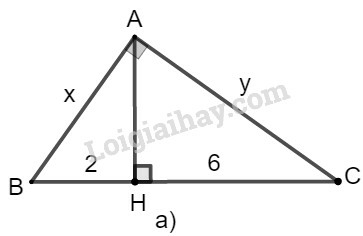
Xét tam giác ABC vuông tại A, đường cao AH.
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2=BH.BC hay x2=2.(2+6)=2.8=16⇒x=4
AC2=CH.BC hay y2=6.(2+6)=6.8=48⇒y=48=43
b) Đặt tên hình như hình dưới đây:
Xét tam giác ABC vuông tại A, đường cao AH.
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có:
AH2=HB.HC hay x2=2.8=16⇒x=4
Bài 3 trang 103 SBT Toán 9 tập 1: Hãy tính x và y trong các hình sau:
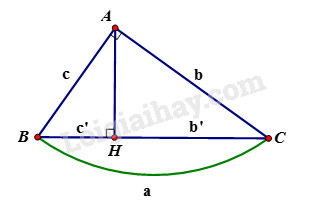
Phương pháp giải:
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+)AC2=CH.BC hay b2=ab′
+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)
Lời giải:
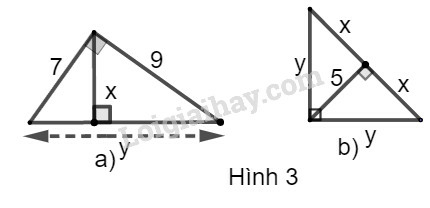
a) Hình a
Theo định lý Pi-ta-go, ta có:
y2=72+92⇒y=72+92=130
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
x.y=7.9⇒x=7.9y=63130
b) Hình b
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
52=x.x=x2⇒x=5
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
y2=x.(x+x)=5.(5+5)=50⇒y=50=52
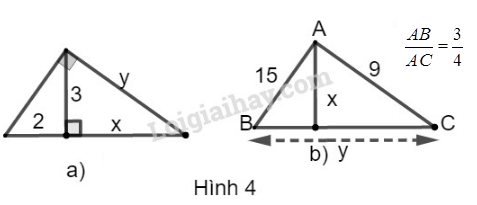
Phương pháp giải:
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+) AC2=CH.BC hay b2=ab′
+) AH.BC=AB.AC
+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)
Lời giải:
a) Hình a
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
32=2.x⇒x=322=92=4,5
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
y2=x.(x+2)=4,5.(4,5+2)⇒y2=29,25⇒y=29,25
b) Hình b
Ta có:
ABAC=34⇒AB3=AC4⇒AC=4.AB3=4.153=4.5=20
Theo định lý Pi-ta-go, ta có:
y2=BC2=AB2+AC2=152+202=625
Suy ra:
y=625=25
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
x.y=15.20⇒x=15.20y=15.2025=12
Giải bài toán trong mỗi trường hợp sau:
a) Cho AH=16,BH=25. Tính AB,AC,BC,CH
b) Cho AB=12,BH=6. Tính AH,AC,BC,CH.
Phương pháp giải:
Để giải bài toán ta áp dụng các công thức sau:
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+) AC2=CH.BC hay b2=ab′
+) AH2=HB.HC;AB.AC=AH.BC
+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)
Lời giải:
a)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: AH2=BH.CH
⇒CH=AH2BH=16225=10,24
BC=BH+CH=25+10,24=35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2=BH.BC⇒AB=BH.BC=25.35,24=881≈29,68
AC2=HC.BC⇒AC=CH.BC=10,24.35,24=360,9≈18,99
b)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2=BH.BC⇒BC=AB2BH=1226=24
CH=BC−BH=24−6=18
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AC2=HC.BC⇒AC=CH.BC=18.24=432≈20,78
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
AH2=HB.HC⇒AH=HB.HC=6.18=108=63
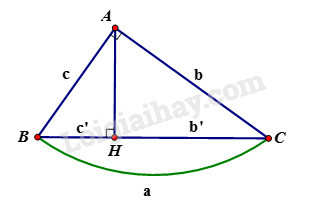
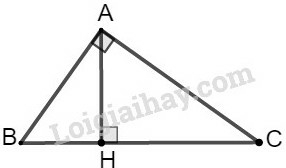
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+) AC2=CH.BC hay b2=ab′
+) AH2=HB.HC;AB.AC=AH.BC
+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)
Lời giải:
Ta vẽ được hình dưới đây:
Giả sử tam giác ABC có: BAC^=90∘
AB=5,AC=7
Theo định lý Py-ta-go, ta có:
BC2=AB2+AC2
⇒BC=AB2+AC2=52+72=74
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
AH.BC=AB.AC⇒AH=AB.ACBC=5.774=3574
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
AB2=BH.BC⇒BH=AB2BC=5274=2574
CH=BC−BH=74−2574=74−2574=4974
Bài 7 trang 103 SBT Toán 9 tập 1: Đường cao của một tam giác vuông chia cạnh huyền thành hai đường thẳng có độ dài là 3 và 4. Hãy tính các cạnh góc vuông của tam giác này.
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
+) AB2=BH.BC hay c2=a.c′
+)AC2=CH.BC hay b2=ab′
+) AB2+AC2=BC2 hay c2+b2=a2 (định lý Pytago)
Lời giải:
Giả sử tam giác ABC có: BAC^=900,AH⊥BC,BH=3,CH=4
Ta có BC=BH+CH=3+4=7
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2=BH.BC=3.7=21⇒AB=21;
AC2=CH.BC=4.7=28⇒AC=28=27.
Bài 8 trang 103 SBT Toán 9 tập 1: Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm và tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các cạnh của tam giác vuông này.
6
Phương pháp giải:
Xét tam giác ABC vuông tại A.
Để giải bài toán ta thực hiện các bước sau:
Bước 1: Thực hiện liên kết các dữ kiện:
BC−AB=1(cm)
AB+AC−BC=4(cm)
Bước 2: Cộng vế với vế để tìm ra một cạnh trong tam giác.
Bước 3: Sử dụng định lí Pytago để tìm các cạnh còn lại của tam giác.
Lời giải:
Giả sử tam giác ABC có BAC^=90∘
Theo đề bài, ta có: BC−AB=1(cm) (1)
AB+AC−BC=4(cm) (2)
Từ (1) và (2) suy ra:
(BC−AB)+(AB+AC−BC)=1+4
⇔BC−AB+AB+AC−BC=5
⇔AC=5
Theo định lý Pytago, ta có: BC2=AB2+AC2 (3)
Từ (1) suy ra: BC=AB+1 (4)
Thay (4) và (3) ta có:
(AB+1)2=AB2+AC2⇔AB2+2AB+1=AB2+52⇔2AB=24⇔AB=12(cm)
Thay AB=12 (cm) vào (1) ta có: BC=12+1=13(cm)
Phương pháp giải:
Xét tam giác ABC có BAC^=900,AH⊥BC,BC=5,AH=2 và BH<CH
Suy luận để có BH+CH=5
Sử dụng hệ thức: BH.CH=AH2
Từ đó tính được BH, suy ra cạnh AB và lập luận để có AB là cạnh nhỏ nhất.
Lời giải:
Giả sử tam giác ABC có BAC^=900,AH⊥BC,BC=5,AH=2 và BH<CH
Ta có: BH+CH=BC=5 nên BH=5−CH (1)
Theo hệ thức liên hệ giữa đường cao và các hình chiếu cạnh góc vuông trong tam giác vuông, ta có:
BH.CH=AH2=22=4 (2)
Từ (1) và (2) suy ra:
BH(5−BH)=4
⇔BH2−5BH+4=0
⇔BH2−4BH−BH+4=0
⇔BH(BH−4)−(BH−4)=0
⇔(BH−1)(BH−4)=0
⇔[BH=1⇒CH=4BH=4⇒CH=1
Do BH<CH nên BH=1 và CH=4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2=BH.BC=1.5=5
Suy ra: AB=5.
Vì BH<CH nên AB<AC hay AB=5 là cạnh nhỏ nhất của tam giác ABC.
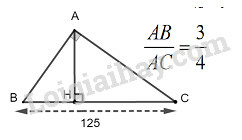
Bài 10 trang 104 SBT Toán 9 tập 1: Cho một tam giác vuông. Biết tỷ số hai cạnh góc vuông là 3:4 và cạnh huyền là 125cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.
Áp dụng tính chất dãy tỉ số bằng nhau:
ab=cd=a+cb+d
Cho tam giác ABC vuông tại A, đường cao AH.
Khi đó ta có các hệ thức sau:
+) AB2=BH.BC
+) AC2=CH.BC
+) AB2+AC2=BC2 (định lý Pytago).
Lời giải:
Giả sử ΔABC vuông tại A chiều cao AH,BC=125cm và ABAC=34
Từ ABAC=34 suy ra: AB3=AC4⇒AB29=AC216
Theo tính chất dãy tỉ số bằng nhau, ta có:
AB29=AC216=AB2+AC29+16=AB2+AC225(1)
Theo định lí Pytago, ta có:
BC2=AB2+AC2⇒AB2+AC2=1252=15625(2)
Từ (1) và (2) suy ra: AB29=AC216=AB2+AC225=1562525=625
Suy ra :
AB2=9.625=5625⇒AB=5625=75(cm)
AC2=16.625=10000⇒AC=10000=100(cm)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2=BH.BC⇒BH=AB2BC=752125=45(cm)
CH=BC−BH=125−45=80(cm).
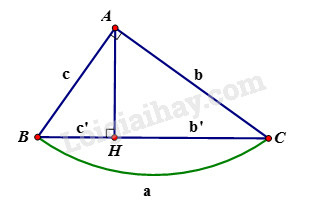
Cho tam giác ABC vuông tại A, đường cao AH.
Khi đó ta có các hệ thức sau:
+) AB2=BH.BC
+) AC2=CH.BC
+) AH2=HB.HC;AB.AC=AH.BC
+) AB2+AC2=BC2 (định lý Pytago).
Lời giải:
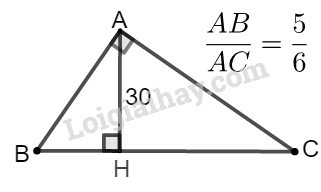
Xét hai tam giác vuông AHB và CHA, ta có:
AHB^=CHA^=900
ABH^=CAH^ (hai góc cùng phụ ACB^)
Vậy ∆AHB∽∆CHA (g.g)
Suy ra: AHHC=ABCA. (1)
Theo đề bài: ABAC=56 và AH=30(cm) (2)
Từ (1) và (2) suy ra: 30HC=56⇒HC=30.65=36(cm)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
AH2=HB.HC⇒HB=AH2HC=30236=25(cm)
Bài 12 trang 104 SBT Toán 9 tập 1: Hai vệ tinh đang bay ở vị trí A và B cùng cách mặt đất 230km có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là 2200km? Biết rằng bán kính R của Trái Đất gần bằng 6370km và hai vệ tinh nhìn thấy nhau nếu OH>R.
Phương pháp giải:
Sử dụng: Tam giác ABC vuông tại A, ta có AB2+AC2=BC2 (định lý Pytago).
Lời giải:
Vì hai vệ tinh cùng cách mặt đất 230km nên tam giác AOB cân tại O.
Ta có: OA=R+230
=6370+230=6600(km)
Trong tam giác cân AOB ta có: OH⊥AB nên H là trung điểm của AB
Suy ra: HA=HB=AB2=22002=1100(km)
Áp dụng định lí Pytago vào tam giác vuông AHO ta có: AO2=AH2+OH2
Suy ra: OH2=OA2−AH2
Suy ra:
OH=OA2−AH2=66002−11002=42350000≈6508(km)
Vì OH>R nên hai vệ tinh nhìn thấy nhau.
a) a2+b2
b) a2−b2,(a>b)
Phương pháp giải:
Áp dụng định lí Pytago vào tam giác OAB vuông tại O, ta có:
AB2=OA2+OB2
Lời giải:
a)
* Cách dựng:
− Dựng góc vuông xOy.
− Trên tia Ox, dựng đoạn OA=a.
− Trên tia Oy, dựng đoạn OB=b.
− Nối AB ta có đoạn AB=a2+b2 cần dựng.
* Chứng minh:
Áp dụng định lý Pytago vào tam giác vuông AOB, ta có:
AB2=OA2+OB2=a2+b2
Suy ra: AB=a2+b2.
b)
* Cách dựng :
− Dựng góc vuông xOy.
− Trên tia Oy, dựng đoạn OA=b.
− Dựng cung tròn tâm A, bán kính bằng a cắt tia Ox tại B.
Ta có đoạn OB=a2−b2(a>b) cần dựng.
* Chứng minh;
Áp dụng định lí Pytago vào tam giác vuông AOB, ta có:
AB2=OA2+OB2⇒OB2=AB2−OA2=a2−b2
Suy ra: OB=a2−b2
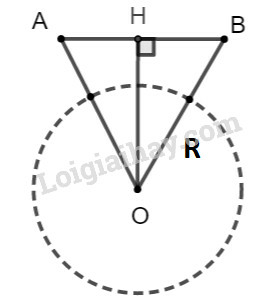
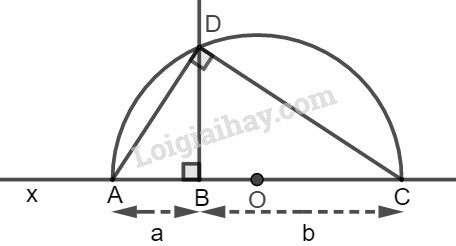
Bài 14 trang 104 SBT Toán 9 tập 1: Cho hai đoạn thẳng có độ dài là a và b. Dựng đoạn thẳng ab như thế nào?
Cho tam giác ABC vuông tại A, đường cao AH.
Khi đó ta có hệ thức sau: AH2=BH.CH
Từ đó suy ra cách dựng hình thỏa mãn đề bài.
Lời giải:
* Cách dựng:
− Dựng đường thẳng x.
− Trên đường thẳng x dựng liên tiếp hai đoạn thẳng AB=a, BC=b.
− Dựng nửa đường tròn tâm O đường kính AC.
− Từ B dựng đường thẳng vuông góc với AC cắt nửa đường tròn tâm O tại D.
Ta có đoạn BD=ab cần dựng.
* Chứng minh:
Nối DA và DC. Ta có tam giác ACD vuông tại D (do OD=OA=OC=AC2) và DB⊥AC.
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
BD2=AB.BC=a.b
Suy ra: BD=ab.
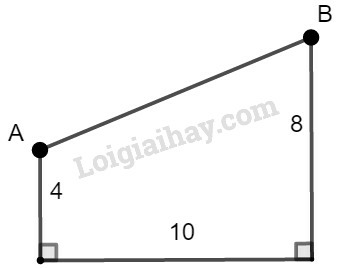
Phương pháp giải:
Áp dụng định lí Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải:
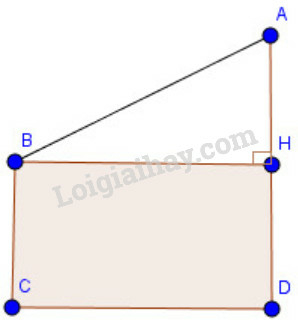
Kẻ BH⊥AD ta được tứ giác BCDH là hình chữ nhật (vì C^=D^=H^=900).
Suy ra DH=BC=4m và BH=CD=10m (tính chất hình chữ nhật)
Và AH=AD−DH=8−4=4(m)
Áp dụng định lý Pytago vào tam giác vuông ABH, ta có:
AB2=BH2+AH2
Suy ra: AB=BH2+AH2=102+42=116≈10,8(m)
Vậy băng chuyền dài khoảng
Định lí Pytago đảo:
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.
Lời giải:
Ta có: 52+122=25+144=169=132
Vì tam giác có ba cạnh với độ dài các cạnh thỏa mãn định lý Pytago đảo (bình phương một cạnh bằng tổng bình phương hai cạnh còn lại) nên nó là tam giác vuông.
Vậy góc đối diện với cạnh 13 (cạnh dài nhất) là góc vuông.
Áp dụng định lí Pytago trong tam giác vuông ABC:
Cho tam giác ABC vuông tại A thì ta có:
BC2=AC2+AB2
Áp dụng tính chất dãy tỉ số bằng nhau:
ab=cd=a+cb+d
Áp dụng tính chất đường phân giác của tam giác.
Lời giải:
Trong tam giác ABC, gọi giao điểm đường phân giác của góc ABC^ với cạnh AC là E.
Theo đề bài ta có:
AE=427m,EC=557m.
Theo tính chất của đường phân giác, ta có: AEEC=ABBC
Suy ra:
ABBC=427557=307407=34
Suy ra: AB3=BC4⇒AB29=BC216
Ta có AC=AE+EC=427+557=10
Áp dụng định lý Pytago vào tam giác vuông ABC, ta có:
AB2+BC2=AC2=102=100
Khi đó, ap dụng tính chất dãy tỉ số bằng nhau:
AB29=BC216=AB2+BC29+16=AB2+BC225=10025=4
Suy ra: AB2=9.4=36⇒AB=36=6(m)
BC2=16.4=64⇒BC=64=8(m)
Vậy: AB=CD=6m
BC=AD=8m.
Áp dụng định lí Pytago trong tam giác vuông ABC:
Cho tam giác ABC vuông tại A thì ta có:
BC2=AC2+AB2
Áp dụng tính chất dãy tỉ số bằng nhau:
ab=cd=a+cb+d
ab=cd⇒a2b2=c2d2=a2+c2b2+d2
Lưu ý: Tỉ số đồng dạng của hai tam giác bằng tỉ số chu vi của hai tam giác đó.
Lời giải:
Gọi a,b,c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b=30cm,c=40cm.
Xét hai tam giác vuông AHB và CHA, ta có:
AHB^=CHA^=90∘
ABH^=CAH^ (hai góc cùng phụ ACB^)
Vậy ΔAHB đồng dạng ΔCHA (g.g)
Suy ra: HBHA=HAHC=BAAC=HB+HA+BAHA+HC+AC=bc
Suy ra: BAAC=bc=3040=34
Suy ra: BA3=AC4⇒BA29=AC216=BA2+AC29+16=BA2+AC225
Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
BC2=AB2+AC2
Suy ra:
BA29=AC216=BC225⇒BA3=AC4=BC5
Xét hai tam giác vuông AHB và CAB, ta có:
CAB^=CHA^=90∘
C^ chung
Nên ΔCAB đồng dạng ΔCHA (g.g)
Suy ra các tam giác ABH,CAH,CBA đồng dạng với nhau nên:
b:c:a=BA:AC:BC=3:4:5
Suy ra: b3=c4=a5⇔303=404=a5
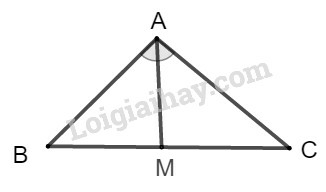
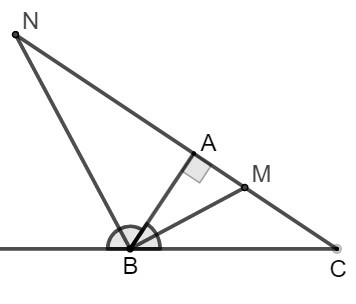
+ Tính chất đường phân giác:
– Đường phân giác trong của một tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
Xét tam giác ABC có AM là phân giác của góc trong BAC^.
Ta có hệ thức: ABAC=AMMC
– Đường phân giác ngoài tại một đỉnh của tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.
+ Tính chất tỉ lệ thức:
ab=cd⇒aa+b=cc+d.
Lời giải:
Vì BM là đường phân giác của góc B nên ta có:
MAMC=ABBC⇒MAMA+MC=ABAB+BC (tính chất tỉ lệ thức)
Suy ra: MA=AB.(MA+MC)AB+BC=AB.ACAB+BC=6.86+10=4816=3(cm)
Vì BM,BN lần lượt là đường phân giác của góc trong và góc ngoài tại đỉnh B nên ta có: BM⊥BN
Suy ra tam giác BMN vuông tại B.
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: AB2=AM.AN
Suy ra: AN=AB2AM=623=363=12(cm)
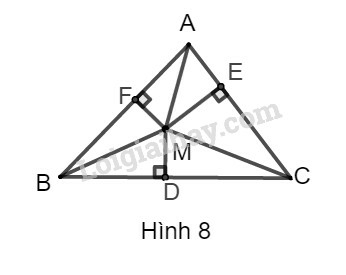
Bài 20 trang 105 SBT Toán 9 tập 1: Cho tam giác vuông ABC. Từ một điểm M bất kì trong tam giác kẻ MD,ME,MF lần lượt vuông góc với các cạnh BC,AC,AB. Chứng minh rằng:
BD2+CE2+AF2=DC2+EA2+FB2.
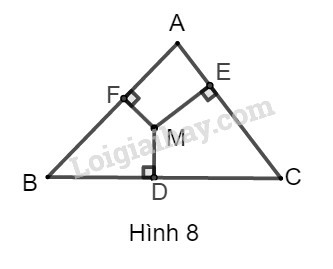
Phương pháp giải:
– Vẽ hình phụ tạo thành các tam giác vuông (với bài toán này ta nối các điểm tạo thành các cạnh AM,BM,CM).
– Xét các tam giác vuông, sử dụng định lý Pytago tạo thành các đẳng thức phù hợp.
– Tìm mối liên hệ giữa các đẳng thức vừa được tạo thành và đẳng thức cần được chứng minh của bài toán.
Sử dụng: Định lý Pytago: Cho tam giác ABC vuông tại A, ta có: BC2=AB2+AC2
Lời giải:
Nối AM,CM,BM ta được hình dưới đây:
Áp dụng định lí Pytago vào tam giác vuông BDM, ta có:
BM2=BD2+DM2⇒BD2=BM2−DM2 (1)
Áp dụng đinh lí Pytago vào tam giác vuông CEM, ta có:
CM2=CE2+EM2⇒CE2=CM2−EM2 (2)
Áp dụng định lí Pytago vào tam giác vuông AFM, ta có:
AM2=AF2+FM2⇒AF2=AM2−FM2 (3)
Cộng từng vế của (1), (2) và (3) ta có:
BD2+CE2+AF2
=BM2−DM2+CM2−EM2+AM2−FM2 (4)
Áp dụng định lí Pytago vào tam giác vuông BFM, ta có:
BM2=BF2+FM2 (5)
Áp dụng định lí Pytago vào tam giác vuông CDM, ta có:
CM2=CD2+DM2 (6)
Áp dụng định lí Pytago vào tam giác vuông AEM, ta có:
AM2=AE2+EM2 (7)
Thay (5), (6), (7) vào (4) ta có:
BD2+CE2+AF2=BF2+FM2−DM2+CD2+DM2−EM2+AE2+EM2−FM2=DC2+EA2+FB2
Vậy BD2+CE2+AF2=DC2+EA2+FB2.
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)