tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Ôn tập chương 2: Đường tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Ôn tập chương 2: Đường tròn
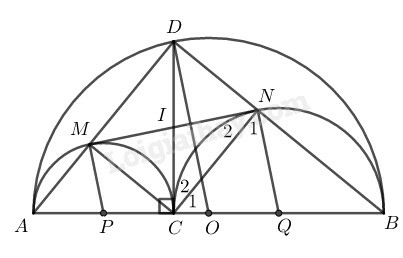
a) Tứ giác DMCN là hình gì? Vì sao ?
b) Chứng minh hệ thức DM.DA=DN.DB.
c) Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB.
d) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ?
Phương pháp giải:
Sử dụng kiến thức:
+) Tứ giác có ba góc vuông là hình chữ nhật.
+) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
+) Trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
a) Tam giác ABD nội tiếp trong đường tròn có AB là đường kính nên BDA^=90∘ hay MDN^=90∘
Tam giác ACM nội tiếp đường tròn có AC là đường kính nên AMC^=90∘
Suy ra: CM⊥AD⇒CMD^=90∘
Tam giác BCN nội tiếp trong đường tròn có BC là đường kính nên BNC^=90∘
Suy ra: CN⊥BD⇒CND^=90∘
Tứ giác CMDN có ba góc vuông nên nó là hình chữ nhật.
b) Tam giác ACD vuông tại C có CM⊥AD.
Theo hệ thức lượng trong tam giác vuông, ta có:
CD2=DM.DA (1)
Tam giác BCD vuông tại C có CN⊥BD.
Theo hệ thức lượng trong tam giác vuông, ta có:
CD2=DN.DB (2)
Từ (1) và (2) suy ra: DM.DA=DN.DB
c) Gọi P là trung điểm của AC,Q là trung điểm của BC,I là giao điểm của MN với DC.
Vì CMDN là hình chữ nhật nên IC=IM=ID=IN
Tam giác CNI cân tại I nên ICN^=INC^ (3)
Tam giác CNQ cân tại Q nên QCN^=QNC^ (4)
Vì AB⊥CD nên ICN^+QCN^=90∘ (5)
Từ (3),(4) và (5) suy ra: INC^+QNC^=90∘ hay MN⊥QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC.
Tam giác CMI cân tại I nên ICM^=IMC^ (6)
Tam giác CMP cân tại P nên PCM^=PMC^ (7)
Vì AB⊥CD nên PCM^+ICM^=90∘ (8)
Từ (6),(7) và (8) suy ra: PMC^+IMC^=90∘ hay MN⊥PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC.
d) Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD=MN
Trong tam giác OCD ta có: CD≤OD nên MN≤OD
Vì OD không đổi nên MN=OD là giá trị lớn nhất khi và chỉ khi C trùng với O.
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.
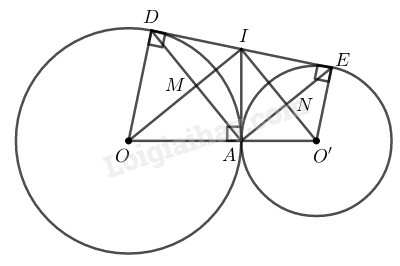
a) Tứ giác AMIN là hình gì ? Vì sao ?
b) Chứng minh hệ thức IM.IO=IN.IO′.
c) Chứng minh rằng OO′ là tiếp tuyến của đường tròn có đường kính là DE.
d) Tính độ dài DE biết rằng OA=5cm,O′A=3,2cm.
Phương pháp giải:
Sử dụng kiến thức:
∗) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
∗) Tứ giác có ba góc vuông là hình chữ nhật.
∗) Hệ thức lượng trong tam giác vuông:
+) Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
+) Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu hai cạnh góc vuông trên cạnh huyền.
Lời giải:
a) Trong đường tròn (O) ta có OI là tia phân giác của góc AID ( tính chất hai tiếp tuyến cắt nhau IA và ID)
Trong đường tròn (O′) ta có O′I là tia phân giác của góc AIE (tính chất hai tiếp tuyến cắt nhau IA và IE)
Mà góc AID và góc AIE là hai góc kề bù nên IO⊥IO′ ( tính chất hai góc kề bù)
⇒ OIO′^=90∘ hay MIN^=90∘
Xét đường tròn (O) có IA=ID ((tính chất hai tiếp tuyến cắt nhau IA và ID)
⇒ Tam giác ADI cân tại I.
Tam giác ADI cân tại I có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID.
⇒ IO⊥AD hay AMI^=90∘
Xét đường tròn (O’) có IA=IE (tính chất hai tiếp tuyến cắt nhau IA và IE)
⇒ Tam giác AEI cân tại I.
Tam giác cân AIE có IO′ là phân giác của góc AIE nên IO′ cũng là đường cao của tam giác AIE.
⇒ IO′⊥AE hay ANI^=90∘
Tứ giác AMIN là hình chữ nhật ( Tứ giác có ba góc vuông)
b) Tam giác AIO vuông tại A có AM⊥IO.
Theo hệ thức lượng trong tam giác vuông AIO, ta có:
IA2=IM.IO(1)
Tam giác AIO′ vuông tại A có AN⊥IO′.
Theo hệ thức lượng trong tam giác vuông AIO′ , ta có:
IA2=IN.IO′(2)
Từ (1) và (2) suy ra: IM.IO=IN.IO′
c) Ta có: IA=ID và IA=IE ( chứng minh trên) nên IA=ID=IE=DE2
⇒ A nằm trên đường tròn tâm I đường kính DE.
Vì OO′⊥IA tại A nên OO′ là tiếp tuyến của đường tròn (I;DE2).
d) Tam giác O′IO vuông tại I có IA⊥OO′.
Theo hệ thức lượng trong tam giác vuông O′IO, ta có:
IA2=OA.O′A=5.3,2=16
⇒ IA=4(cm).
Mà IA=DE2⇒DE=2IA nên DE=2.4=8(cm).
Sử dụng kiến thức:
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có ba góc vuông là hình chữ nhật.
Lời giải:
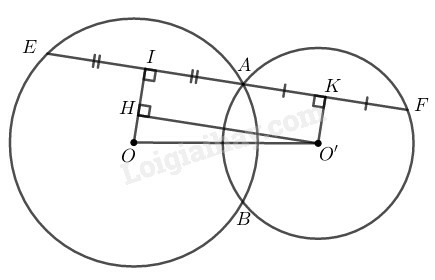
Kẻ OI⊥AE,O′K⊥AF
Trong đường tròn (O), có OI⊥AE mà OI là 1 phần đường kính và AE là dây cung nên:
IA=IE=12AE ( đường kính vuông góc với dây cung)
Trong đường tròn (O′), có O′K⊥AF mà O’K là 1 phần đường kính và AF là dây cung nên:
KA=KF=12AF (đường kính vuông góc với dây cung)
Ta có: EF=AE+AF
Suy ra: EF=2IA+2AK=2(IA+AK)=2IK(1)
Kẻ O′H⊥OI
Khi đó tứ giác IHO′K là hình chữ nhật ( có ba góc vuông)
Suy ra: O′H=IK
Trong tam giác OHO′ ta có: O′H≤OO′=3(cm)
Suy ra: IK≤OO′ (2)
Từ (1) và (2) suy ra: EF≤2OO′=6(cm)
Ta có: EF=6cm khi H và O trùng nhau hay EF//OO′
Vậy EF có độ dài lớn nhất bằng 6cm khi và chỉ khi EF//OO′.
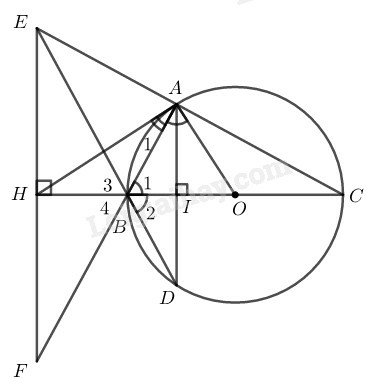
a) Tam giác EBF là tam giác cân ;
b) Tam giác HAF là tam giác cân ;
c) HA là tiếp tuyến của đường tròn (O).
Phương pháp giải:
Sử dụng kiến thức:
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Trong tam giác cân, đường cao ứng với cạnh đáy cũng là đường phân giác, trung tuyến, trung trực.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
a) Gọi I là giao điểm của AD và BC.
Xét đường tròn (O) có đường kính BC⊥AD tại I nên I là trung điểm của dây AD (định lý)
Suy ra BC là đường trung trực của AD nên theo tính chất đường trung trực ta có: BA=BD
Tam giác BAD cân tại B có BI⊥AD nên BI là tia phân giác của góc ABD.
Suy ra: ABI^=DBI^
Mà ABI^=HBF^ (đối đỉnh)
và DBI^=HBE^ ( đối đỉnh)
Suy ra: HBE^=HBF^
Do đó BH là tia phân giác của góc EBF
Tam giác EBF có BH là tia phân giác của góc EBF và BH⊥EF nên tam giác EBF cân tại B.
b) Tam giác EBF cân tại B có BH là đường cao nên BH cũng là đường trung tuyến.
Suy ra HE=HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên:
HA=HE=HF=12EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
c) Tam giác AHF cân tại H nên HAF^=HFA^ (1)
Tam giác AOB cân tại O nên OAB^=OBA^
Mà ABI^=HBF^ ( đối đỉnh)
Suy ra: OAB^=HBF^ (2)
Từ (1) và (2) suy ra: HAO^=HAF^+OAB^=HFB^+HBF^ (3)
Tam giác BHF vuông tại H nên HFB^+HBF^=90∘ (4)
Từ (3) và (4) suy ra: HAO^=90∘ hay HA⊥AO
Vậy HA là tiếp tuyến của đường tròn (O).
a) Chứng minh rằng NE⊥AB.
b) Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O).
c) Chứng minh rằng FN là tiếp tuyến của đường tròn (B;BA).
Phương pháp giải:
Sử dụng kiến thức:
+) Tam giác nội tiếp đường tròn, có một cạnh là đường kính thì tam giác đó là tam giác vuông.
+) Trong tam giác, ba đường cao cắt nhau tại một điểm gọi là trực tâm tam giác.
+) Hai điểm gọi là đối xứng với nhau qua O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
a) Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: AN⊥BM
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại C
Suy ra: AC⊥BN
Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trực tâm của tam giác ABN
Suy ra: NE⊥AB
b) Ta có: MA=MN ( tính chất đối xứng tâm)
ME=MF ( tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi điểm đường nên nó là hình bình hành.
Suy ra: AF//NE
Mà NE⊥AB ( chứng minh trên)
Suy ra: AF⊥AB tại A.
Vậy FA là tiếp tuyến của đường tròn (O).
c) Trong tam giác ABN ta có: AN⊥BM và AM=MN hay BM vừa là đường cao vừa là đường trung tuyến nên tam giác ABN cân tại B.
Suy ra BA=BN hay N thuộc đường tròn (B;BA)
Tứ giác AFNE là hình bình hành nên AE//FN hay FN//AC
Mặt khác: AC⊥BN ( chứng minh trên)
Suy ra: FN⊥BN tại N
Vậy FN là tiếp tuyến của đường tròn (B;BA).
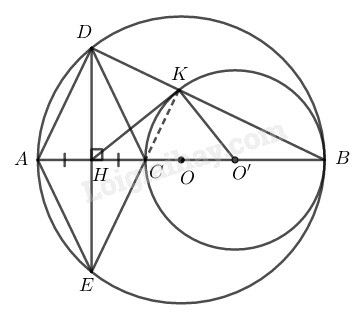
a) Hai đường tròn (O) và (O′) có vị trí tương đối như thế nào đối với nhau ?
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì ? Vì sao?
c) Gọi K là giao điểm của DB và đường tròn (O′). Chứng minh rằng ba điểm E,C,K thẳng hàng.
d) Chứng minh rằng HK là tiếp tuyến của đường tròn (O′).
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu OO′=R–r thì đường tròn (O) và đường tròn (O′) tiếp xúc trong.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc là hình thoi.
+) Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm xác định được hai đường thẳng cùng vuông góc với một đường thẳng thứ ba.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thìđường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
a) Vì O,O′ và B thẳng hàng nên: O′B<OB⇒O′ nằm giữa O và B
Ta có: OO′=OB−O′B
Vậy đường tròn (O′) tiếp xúc trong với đường tròn (O) tại B.
b) Xét đường tròn (O) có AB⊥DE(gt) mà AB là đường kính, DE là dây cung
Suy ra: HD=HE (đường kính vuông góc với dây cung)
Lại có: HA=HC(gt)
Suy ra, tứ giác ADCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: AC⊥DE
Suy ra tứ giác ADCE là hình thoi.
c) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D.
Suy ra: AD⊥BD
Tứ giác ADCE là hình thoi nên EC//AD
Suy ra: EC⊥BD(1)
Tam giác BCK nội tiếp trong đường tròn (O′) có BC là đường kính nên vuông tại K.
Suy ra: CK⊥BD(2)
Từ (1) và (2) suy ra EC trùng với CK
Vậy E,C,K thẳng hàng.
d) Tam giác DEK vuông tại K có KH là trung tuyến ứng với cạnh huyền DE nên:
HK=HE=12DE (tính chất tam giác vuông)
Suy ra tam giác EHK cân tại H
Suy ra: HEK^=HKE^ (tính chất tam giác cân) (3)
Ta có: O′K=O′C (= bán kính đường tròn (O’)) nên tam giác O′CK cân tại O′
Suy ra: O′KC^=O′CK^ (tính chất tam giác cân)
Mà: O′CK^=HCE^ (đối đỉnh)
Suy ra: O′KC^=HCE^ (4)
Từ (3) và (4) suy ra: HKO′^=HKE^+O′KC^=HEK^+HCE^ (5)
Tam giác CEH vuông tại H nên HEK^+HCE^=90∘ (6)
Từ (5) và (6) suy ra: HKO′^=90∘ hay HK⊥KO′ tại K
Vậy HK là tiếp tuyến của đường tròn (O′).
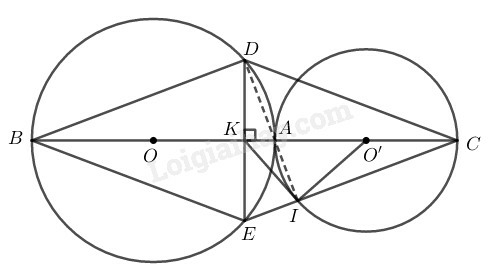
a) Chứng minh rằng tứ giác BDCE là hình thoi.
b) Gọi I là giao điểm của EC và đường tròn (O′). Chứng minh rằng ba điểm D,A,I thẳng hàng.
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O′).
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc là hình thoi.
+) Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm xác định được hai đường thẳng cùng vuông góc với một đường thẳng thứ ba.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
a) Vì đường tròn (O) và (O′) tiếp xúc ngoài tại A nên O,A và O′ thẳng hàng.
Trong đường tròn (O) ta có: AB⊥DE tại K mà AB là đường kính và DE là dây cung
Suy ra: KD=KE ( đường kính vuông góc với dây cung)
Lại có: KB=KC(gt)
Suy ra tứ giác BDCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: BC⊥DE
Suy ra tứ giác BDCE là hình thoi.
b) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D.
Suy ra: AD⊥BD
Tứ giác BDCE là hình thoi nên EC//BD
Suy ra: EC⊥AD(1)
Tam giác AIC nội tiếp trong đường tròn (O′) có AC là đường kính nên vuông tại I.
Suy ra: AI⊥CE(2)
Từ (1) và (2) suy ra AD trùng với AI
Vậy D,A,I thẳng hàng.
c) Tam giác DIE vuông tại I có IK là trung tuyến ứng với cạnh huyền DE nên:
KI=KD=12ED ( tính chất tam giác vuông)
Suy ra tam giác IKD cân tại K
Suy ra: KID^=KDI^ hay KIA^=KDA^ (3)
Ta có: O′A=O′I (= bán kính đường tròn (O’)) nên tam giác O′IA cân tại O′
Suy ra: O′AI^=O′IA^ ( tính chất tam giác cân)
Mà: O′AI^=KAD^ (đối đỉnh)
Suy ra: O′IA^=KAD^ (4)
Từ (3) và (4) suy ra: KIO′^=KIA^+AIO′^=KDA^+KAD^
Xét tam giác KAD vuông tại K có: KDA^+KAD^=900
Suy ra KIO′^=90∘ hay KI⊥O′I tại I.
Vậy KI là tiếp tuyến của đường tròn (O′).
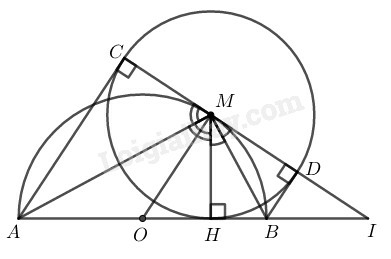
a) Chứng minh rằng ba điểm C,M,D thẳng hàng và CD là tiếp tuyến của đường tròn (O).
b) Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC+BD không đổi.
c) Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi.
Phương pháp giải:
Sử dụng kiến thức:
∗) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
∗) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
∗) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
∗) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hìnhchiếu cạnh góc vuông đó trên cạnh huyền.
Lời giải:
a) Trong đường tròn (M;MH), có AC và AH là 2 tiếp tuyến cắt nhau tại A, theo tính chất hai tiếp tuyến cắt nhau, ta có: MA là tia phân giác của góc HMC và AC=AH
Suy ra: CMA^=HMA^ hay CMH^=2HMA^
Trong đường tròn (M;MH), có BD và BH là 2 tiếp tuyến cắt nhau tại B, theo tính chất hai tiếp tuyến cắt nhau, ta có: MB là tia phân giác của góc HMD và BD=BH
Suy ra: HMB^=DMB^ hay DMH^=2HMB^
Tam giác ABM nội tiếp đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: AMB^=90∘ hay HMA^+HMB^=90∘
Suy ra: CMH^+HMD^=2HMA^+2HMB^
=2(HMA^+HMB^)=2.90∘=180∘
Vậy C,M,D thẳng hàng.
b) Theo câu a) ta có: AC=AH và BD=BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH.
Suy ra: AC+BD=AH+BH=AB không đổi
c) Ta có: AC⊥CD và BD⊥CD ( tính chất tiếp tuyến)
Suy ra: AC//BD hay tứ giác ABDC là hình thang
Mà OA=OB (= bán kính (O))
Và MC=MD (= bán kính (M))
Suy ra OM là đường trung bình của hình thang ABCD
Khi đó OM//AC. Suy ra: OM⊥CD hay OMI^=90∘
Tam giác OMI vuông tại M có MH⊥OI.
Theo hệ thức lượng trong tam giác vuông, ta có: OM2=OH.OI
Mà OM là bán kính đường tròn (O) nên OM có độ dài không đổi.
Suy ra: OH.OI không đổi.
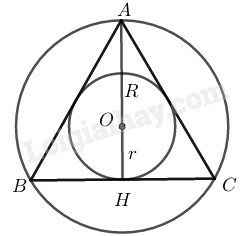
Bài tập bổ sung (trang 173 SBT Toán 9)
(A) 13; (B)12;
(C) 12; (D) 2.
Hãy chọn phương án đúng.
Phương pháp giải:
Sử dụng kiến thức:
+) Trong tam giác đều, giao ba đường trung tuyến cũng là giao ba đường phân giác, ba đường cao, đường trung trực (tâm đường tròn nội tiếp cũng là tâm đường tròn ngoại tiếp).
+) Trọng tâm tam giác cách mỗi đỉnh một khoảng bằng 23 độ dài đường trung tuyến ứng với đỉnh đó.
Lời giải:
Giả sử ΔABC đều ngoại tiếp đường tròn (O,r), nội tiếp đường (O,R)
Gọi H là trung điểm của BC
⇒r=OH,R=OA
Vì O là trọng tâm tam giác ABC (vì tam giác ABC đều)
⇒rR=OHOA=12
Chọn (B).
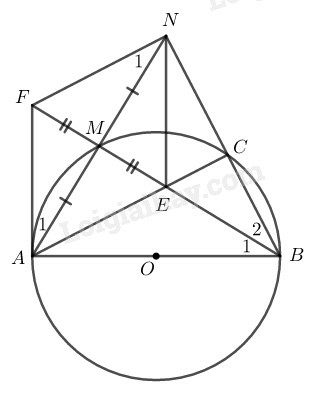
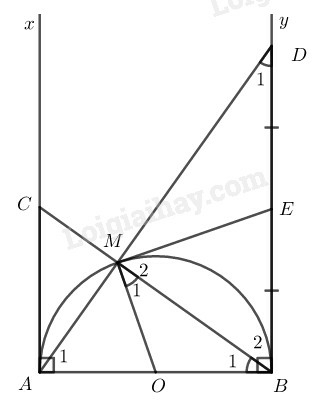
a) AC.BD=AB2;
b) ME là tiếp tuyến của nửa đường tròn.
Phương pháp giải:
a) Chứng minh hai tam giác đồng dạng để thiết lập tỉ số giữa các cạnh, từ đó chứng minh được biểu thức đề bài đưa ra.
b) Theo tính chất của tiếp tuyến, ta phải chứng minh được ME⊥OM tại M.
Áp dụng: Trong tam giác vuông đường trung tuyến ứng với canh huyền thì bằng nửa cạnh huyền.
Từ đó ta tìm các góc bằng nhau, thiết lập mối liên hệ giữa chúng.
Lời giải:
a) Xét tam giác ABD vuông tại B có A1^+D1^=900 (1)
Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính nên vuông tại M.
Suy ra A1^+B1^=900 (2)
Từ (1) và (2) suy ra: B1^=D1^ ( cùng phụ với A1^).
Xét ∆ABC và ∆BDA có:
B1^=D1^ (cmt)
A^=B^=90∘
Suy ra ∆ABC đồng dạng với ∆BDA(g.g) suy ra:
ABBD=ACBA(cặp cạnh tương ứng tỉ lệ), do đó AC.BD=AB2
b) Vì tam giác AMB vuông tại M (cmt) nên AD⊥BM
Suy ra tam giác BMD vuông tại M.
Ta có ∆MBD vuông tại M có ME là đường trung tuyến nên ED=EM=EB
Suy ra ∆EBM cân tại E nên M2^=B2^(1)
Lại có ∆MOB cân tại O (do OM=OB) nên M1^=B1^ (2)
Từ (1) và (2) suy ra
M1^+M2^ = B1^+B2^ =OBD^=90∘
Hay OME^=900 tức là ME⊥OM tại M.
Vậy ME là tiếp tuyến của nửa đường tròn (O).
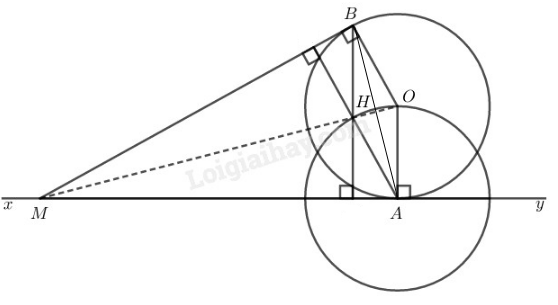
a) Chứng minh rằng ba điểm M,H,O thẳng hàng.
b) Tứ giác AOBH là hình gì ?
c) Khi M di chuyển trên xy thì H di chuyển trên đường nào ?
Phương pháp giải:
a) Để chứng minh M,O,H:
– Ta chứng minh MO⊥AB, MH⊥AB
b) Sử dụng dấu hiệu nhận biết hình thoi (hình bình hành có một cặp cạnh bằng nhau là hình thoi) để chứng minh tứ giác AOBH là hình thoi.
c) Liên kết các dữ kiện và các phần đã được chứng minh để tìm ra dược H cách A một đoạn không đổi,
từ đó tìm được quỹ tích của M khi chuyển động thì H cũng chuyển động trên đường tròn tâm A,
bán kính không đổi.
Lời giải:
a) Vì H là trực tâm của tam giác MAB nên MH⊥AB (1)
Xét đường tròn (O) có MA và MB là 2 tiếp tuyến cắt nhau tại M nên OM là phân giác của góc BOA (tính chất 2 tiếp tuyến cắt nhau)
Lại có OA=OB (= bán kính đường tròn (O)) nên tam giác OAB cân tại O có OM là đường phân giác nên OM cũng là đường cao. Suy ra OM⊥AB (2)
Từ (1) và (2) suy ra MH và MO đều vuông góc với AB nên M,H,O thẳng hàng.
b) Xét đường tròn (O) có MB, MA là tiếp tuyến nên OB⊥MB,OA⊥MA
Xét tam giác MAB có H là trực tâm nên AH⊥MB,BH⊥MA
Tứ giác AOBH có
BH//OA (cùng vuông góc với MA),
AH//OB (cùng vuông góc với MB).
Suy ra tứ giác AOBH là hình bình hành, mà OA=OB (cmt) nên tứ giác AOBH là hình thoi.
c) Ta có HA=OA (do AOBH là hình thoi),
Nên H cách A cố định một khoảng bằng OA không đổi.
Như vậy, khi M chuyển động trên xy thì H di chuyển trên đường tròn (A;AO).
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)