tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài tập ôn chương 3: Góc với đường tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài tập ôn chương 3: Góc với đường tròn
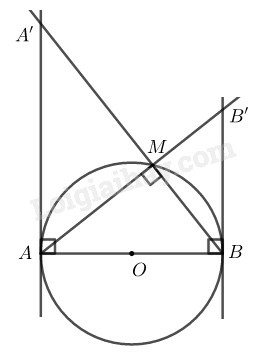
a) Chứng minh rằng AA′.BB′=AB2
b) Chứng minh rằng
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu hai tam giác đồng dạng ta suy ra các cạnh tương ứng tỉ lệ.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Lời giải:
a) Xét ∆AA′B và ∆BB′A:
A′AB^=B′BA^=900
BB′A^=ABA′^ (vì cùng phụ với BAB′^)
Suy ra: ∆AA′B đồng dạng ∆BAB′(g.g)
AA′BA=ABBB⇒AA′.BB′=AB2
b) AMB^=900 (góc nội tiếp chắn nửa đường tròn)
⇒AM⊥A′B
∆AA′B vuông tại A. Theo hệ thức lượng trong tam giác vuông ta có:
AA′2=A′M.A′B
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.
+) Số đo của nửa đường tròn bằng 180o.
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Trong hình thoi, hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải:
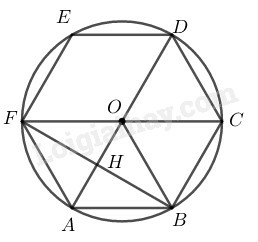
Lục giác đều ABCDEF nội tiếp trong đường tròn (O)
AB⏜=CB⏜=CD⏜=DE⏜=EF⏜=FA⏜=60∘
⇒ sđABCD⏜=sđAB⏜+sđBC⏜+sđCD⏜=180∘
Nên AD là đường kính của đường tròn (O)
Ta có: OA=OB=OF=AB=AF=R
Nên tứ giác ABOF là hình thoi
Gọi giao điểm của AD và BF là H
Ta có: FB⊥OA (tính chất hình thoi)
⇒AH=HO=AO2=R2
HD=HO+OD=R2+R=3R2
Suy ra: AHHD=R23R2=13
Phương pháp giải:
* Phân tích:
+) Giả sử đã có một hình thỏa mãn điều kiện bài toán
+) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,…)
+) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)
* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.
Lời giải:
Phân tích:
Giả sử M là điểm nằm trong ∆ABC sao cho AMB^=BMC^=CMA^
Vì AMB^+BMC^+CMA^=360∘
Nên AMB^=BMC^=CMA^=360∘:3=1200
Khi đó, điểm M nhìn các cạnh AB,BC,AC của ∆ABC dưới 1 góc bằng 120∘
Cách dựng:
– Dựng cung chứa góc 120∘ vẽ trên đoạn BC.
– Dựng cung chứa góc 120∘ vẽ trên đoạn AC.
– Giao điểm thứ hai ngoài C của hai cung này là điểm M phải dựng.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với cotang góc kề.
+) Trong đường tròn R, độ dài l của một cung n∘ được tính theo công thức: l=πRn180.
Lời giải:
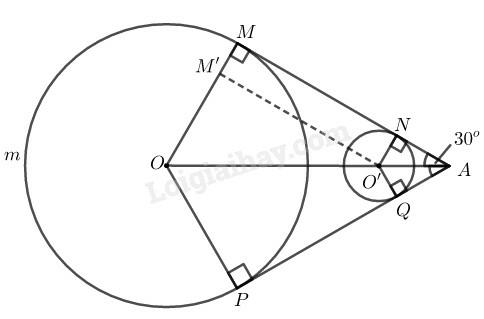
+) Vì hai tiếp tuyến chung của đường tròn (O) và (O′) cắt nhau tại A nên O,O′,A thẳng hàng.
OAM^=OAP^=12MAP^ (tính chất hai tiếp tuyến cắt nhau)
⇒OAM^=300
+) Trong tam giác vuông OMA có OMA^=900
⇒MA=OM.cotOAM^
=4acot300=4a3
+) Trong tam giác vuông O′NA có O′NA^=900
⇒NA=O′NcotO′AN^=acot300=a3
Từ đó: MN=MA−NA=4a3−a3=3a3
+) Trong tứ giác O′NAQ có N^=Q^=900; A^=600
Suy ra: NO′Q^=3600−(900+900+600)=1200 (tổng bốn góc trong tứ giác bằng 3600)
Độ dài cung nhỏ NQ⏜ là: l1=π.a.120180=2πa3
+) Trong tứ giác OMAP có M^=P^=900; A^=600
Suy ra: MOP^=3600−(900+900+600)=1200 (tổng bốn góc trong tứ giác bằng 3600) nên số đo cung nhỏ MP⏜ bằng 1200
sđMnP⏜ =3600−1200=2400
Độ dài cung lớn MnP⏜ là l2=π.4a.240180=16πa3
Chiều dài của dây cua – roa mắc qua hai ròng rọc là:
2MN+l1+l2=2.3a3+2πa3+16πa3
=6a3+6πa=6a(3+π)
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc cos góc kề.
+) Diện tích hình thang bằng nửa tổng hai đáy nhân với chiều cao.
+) Diện tích hình quạt tròn bán kính R, cung n∘ được tính theo công thức: S=πR2n360.
Lời giải:
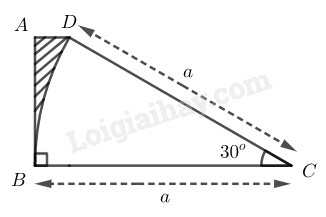
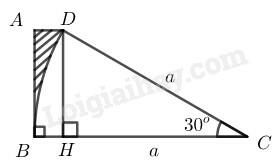
Diện tích phần gạch sọc là hiệu giữa diện tích hình thang ABCD và diện tích hình quạt tròn có góc ở tâm 300 của đường tròn bán kính bằng a.
Từ D kẻ DH⊥BC, suy ra ADHB là hình chữ nhật.
Trong tam giác vuông HDC có DHC^=900
DH=DC.sinC^=a.sin300=a2
CH=DC.cosC^=a.cos300=a32
BH=BC−HC=a−a32=a(2−3)2
⇒AD=BH=a(2−3)2 (do ADHB là hình chữ nhật)
Diện tích của hình thang ABCD bằng:
AD+BC2.DH=a(2−3)2+a2.a2
=a2(4−3)8
Diện tích hình quạt tròn bằng: π.a2.30360=πa212
Diện tích phần gạch sọc:
S=a2(4−3)8−πa12
=3a2(4−3)−2πa224
=a224(12−33−2π)
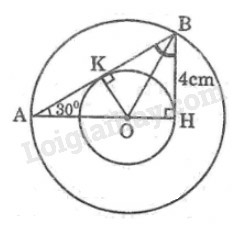
a) Chứng minh đường tròn (O;OH) tiếp xúc với cạnh AB.
b) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Tính chất tia phân giác của một góc: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối.
+) Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng cạnh huyền nhân với cos góc kề.
+) Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2.
Lời giải:
a) Kẻ OK⊥AB tại K
Vì BO là đường phân giác của B^ (gt)
⇒OK=OH (tính chất đường phân giác)
Suy ra: OK cũng là bán kính của đường tròn (O;OH)
Vậy đường tròn (O;OH) tiếp xúc với AB tại K.
b) ΔAHB có H^=900; A^=300
Suy ra: B^=600⇒ABO^=12B^=300
Suy ra: ∆OAB cân tại O nên OB=OA
Vậy B∈(O;OA)
∆BHO có H^=900; OBH^=300
OH=BH.tan300=4.33=433(cm)
OB=BHcosOBH^=4cos300=432=833 (cm)
Diện tích đường tròn nhỏ: S1=π(433)2=16π3 (cm2)
Diện tích đường tròn lớn: S2=π(833)2=64π3 (cm2)
Diện tích hình vành khăn:
S=S2−S1=64π3−16π3=48π3=16π (cm2)
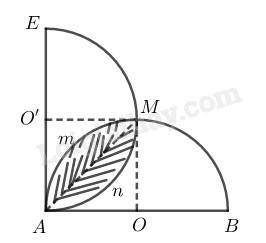
a) Tìm quỹ tích điểm D
b) Tính diện tích phần chung của hai nửa hình tròn đường kính AB và AE.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Hình thoi có một góc vuông là hình vuông.
+) Diện tích hình quạt tròn bán kính R, cung n∘ được tính theo công thức: S=πR2n360.
+) Trong đường tròn R, độ dài l của một cung n∘ được tính theo công thức: l=πRn180.
Lời giải:
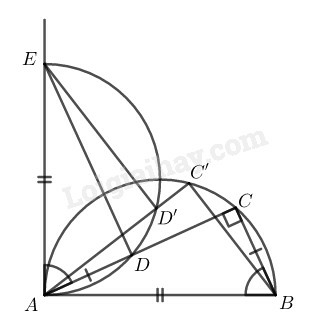
a) Chứng minh thuận
Nối DE. Xét ∆ABC và ∆AED:
AB=AE(gt)
AD=BC(gt)
EAD^=ABC^ (hệ quả góc giữa tia tiếp tuyến và dây cung)
Suy ra: ∆ABC=∆EAD(c.g.c)
⇒EDA^=ACB^
Mà ACB^=900 (góc nội tiếp chắn nửa đường tròn)
⇒EDA^=900
Điểm C chuyển động trên nửa đường tròn đường kính AB thì điểm D luôn nhìn đoạn AE cố định dưới một góc bằng 900 nên điểm D nằm trên nửa đường tròn đường kính AE nằm trong nửa mặt phẳng bờ AE chứa nửa đường tròn đường kính AB.
Chứng minh đảo:
Trên nửa đường tròn đường kính AE lấy điểm D′ bất kỳ, đường thẳng AD′ cắt nửa đường tròn đường kính AB tại C′. Nối ED′,BC′.
Xét ∆AD′E và ∆BC′A:
D′^=C′^=900 (các góc nội tiếp chắn nửa đường tròn)
AE=AB(gt)
EAD^=ABC′^ (2 góc cùng phụ C′AB^)
Suy ra: ∆AD′E=∆BC′A (cạnh huyền, góc nhọn)
⇒AD′=BC′
Vậy khi điểm C chạy trên nửa đường tròn đường kính AB thì quỹ tích điểm D là nửa đường tròn đường kính AE.
b)
Gọi tâm hai nửa đường tròn đường kính AB và AE lần lượt là O và O′, giao điểm thứ hai của hai đường tròn là M
Ta có: OA=OM=O′A=O′M (vì AB=AE)
Suy ra tứ giác AOMO′ là hình thoi.
Ta lại có: A^=900 nên tứ giác AOMO′ là hình vuông
Vậy tứ giác AOMO′ là hình vuông
Diện tích phần chung của hai nửa hình tròn bằng diện tích hai quạt tròn có cung AmM⏜ trừ đi diện tích hình vuông
Diện tích hình quạt tròn AOM bằng:
π(AB2)2.90360=πAB216
Diện tích của hình vuông AOMO′ bằng:
(AB2)2=AB24
Diện tích phần chung bằng:
2.πAB216−AB24=πAB28−2AB28
=AB28(π−2) (đơn vị diện tích)
Bài tập bổ sung (trang 114,115,116 SBT Toán 9)
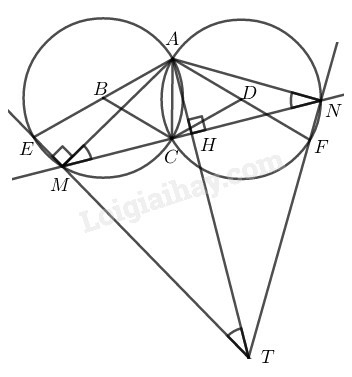
a) MNT là tam giác đều.
b) AT=4AH.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Sử dụng tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải:
a) Trong đường tròn (B) ta có:
AMC^=12ABC^ (hệ quả góc nội tiếp) mà ABC^=60∘ (vì ∆ABC đều)
⇒AMC^=30∘
AME^=90∘ (góc nội tiếp chắn nửa đường tròn (B))
⇒AMT^=90∘
TMN^=AMT^−AMC^=90∘−30∘=60∘
Trong đường tròn (D) ta có:
ANC^=12ADC^ (Hệ quả góc nội tiếp) mà ADC^=60∘ (vì ∆ADC đều) ⇒ANC^=30∘
ANF^=90∘ (góc nội tiếp chắn nửa đường tròn (D))
⇒ANC^+CNF^=90∘
⇒CNF^=90∘−ANC^=90∘−30∘=60∘ hay MNT^=60∘
Vậy ∆TMN đều.
b) AMC^=ANC^=30∘ (theo câu a)
⇒ΔAMN cân tại A ⇒AM=AN nên A nằm trên đường trung trực MN
Vì ∆TMN đều ⇒TM=TN nên T nằm trên đường trung trực MN
Suy ra AT là đường trung trực của MN nên AT⊥MN
∆AHM có AHM^=90∘
AM=AHsinM=AHsin30∘=AH12=2AH (1)
Vì ∆TMN đều có TH⊥MN nên TH cũng là đường phân giác của T^ nên MTA^=30∘
∆AMT có AMT^=90∘
AT=AMsinMTA^=AM12=2AM(2)
Từ (1) và (2) suy ra: AT=2AM=2.2AH=4AH
Vậy AT=4AH.
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong một đường tròn, đường kính đi trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Các đỉnh của một đa giác cùng nhìn một cạnh dưới một góc vuông thì đa giác đó nội tiếp.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải:
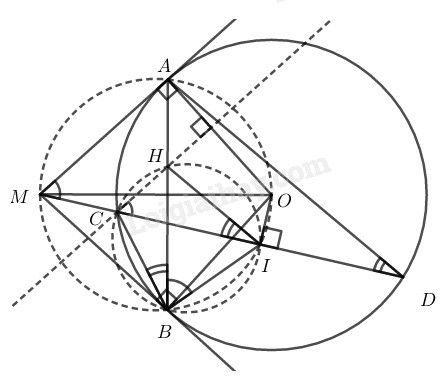
Xét đường tròn (O) có MA⊥OA (tính chất tiếp tuyến)
⇒MAO^=90∘
MB⊥OB (tính chất tiếp tuyến)
⇒MBO^=90∘
Lại có I là trung điểm dây CD (gt) nên IC=ID
⇒OI⊥CD (đường kính đi qua điểm chính giữa của dây không đi qua tâm thì vuông góc với dây đó)
⇒MIO^=90∘
Từ đó: A,B,I nhìn MO cố định dưới một góc bằng 90∘ nên A,B,I nằm trên đường tròn bán kính MO.
⇒AMI^=ABI^ (Hai góc nội tiếp cùng chắn cung nhỏ AOI)
Lại có CH⊥AO(gt) mà MA⊥OA (chứng minh trên)
Suy ra: CH//MA
Do đó: AMI^=HCI^ (hai góc đồng vị)
Suy ra: HCI^=ABI^ (=AMI^) hay HCI^=HBI^
Do đó B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.
⇒CBH^=CIH^ (hai góc nội tiếp cùng chắn cung nhỏ CH⏜) hay CBA^=CIH^(1)
Trong đường tròn (O) ta có:
CBA^=CDA^ (2 góc nội tiếp cùng chắn cung nhỏ AC⏜) (2)
Từ (1) và (2) suy ra: CIH^=CDA^ nên HI//AD (vì có cặp góc ở vị trí đồng vị bằng nhau)
(Trường hợp cát tuyến đi qua tâm thì ngũ giác MAOIB suy biến thành tứ giác MAOB chứng minh tương tự ta có HO//AD).
(A) có đỉnh nằm trên đường tròn.
(B) có hai cạnh là hai dây của đường tròn.
(C) có hai đỉnh là tâm đường tròn và có hai cạnh là hai bán kính.
(D) có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.
Phương pháp giải:
Sử dụng định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Lời giải:
Chọn (D) Góc nội tiếp là góc có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.
(A) đi qua các đỉnh của một tam giác.
(B) tiếp xúc với các đường thẳng chứa các cạnh của một tam giác.
(C) tiếp xúc với các cạnh của một tam giác.
(D) nằm trong một tam giác.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
Lời giải:
Chọn (C) Một đường tròn là đường tròn nội tiếp nếu nó tiếp xúc với các cạnh của một tam giác.
(A) có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.
(B) có 4 góc bằng nhau.
(C) có 4 cạnh bằng nhau.
(D) có các cạnh tiếp xúc với đường tròn.
Phương pháp giải:
Ta sử dụng kiếnt thức: Tứ giác có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau thì tứ giác đó nội tiếp.
Lời giải:
Chọn (A) Một tứ giác là tứ giác nội tiếp nếu có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.
(A) một đường tròn đi qua hai điểm A,B.
(B) một đường thẳng song song với AB.
(C) một cung chứa góc 120∘ dựng trên hai điểm A,B.
(D) hai cung chứa góc 120∘ (đối xứng nhau) dựng trên hai điểm A,B.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Với đoạn thẳng AB và góc α(0∘<α<180∘) cho trước thì quỹ tích các điểm M thỏa mãn AMB^=α là hai cung chứa góc α dựng trên đoạn AB.
+) Hai cung chứa góc α là hai cung tròn đối xứng với nhau qua AB.
Lời giải:
Chọn (D) Quỹ tích các điểm M nhìn đoạn thẳng AB dưới một góc 120∘ là hai cung chứa góc 120∘ (đối xứng nhau) dựng trên hai điểm A,B.
(A) πR; (B) 2πR;
(C) 4πR; (D) 8πR.
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài C của một đường tròn có đường kính d là C=πd.
Lời giải:
Độ dài đường tròn đường kính 8R là:
C=π.8R=8πR
Suy ra độ dài nửa đường tròn đường kính 8R là 4πR
Vây chọn (C) 4πR.
(A)12πR2; (B) πR2;
(C) 2πR2; (D) 4πR2;
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích S của một hình tròn bán kính R được tính theo công thức: S=π.R2
Lời giải:
Bán kính hình tròn có đường kính 4R là 2R
Diện tích S của một hình tròn bán kính 2R là: S=π.(2R)2=4πR2
Suy ra diện tích của nửa hình tròn có đường kính 4R là: 2πR2
Vậy chọn (C) 2πR2
(A) 50∘; (B) 80∘;
(C) 130∘; (D) Không tính được.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
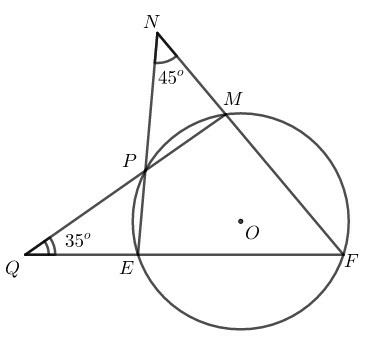
Xé đường tròn (O), ta có: MFE^=12sđME⏜(nhỏ) (góc nội tiếp)
=12(sđPM⏜+sđPE⏜)
Ta có:
+) N^=12(sđEF⏜−sđPM⏜) (góc có đỉnh bên ngoài đường tròn)
⇒sđEF⏜=2N^+sđPM⏜
+) Q^=12(sđMF⏜−sđPE⏜) (góc có đỉnh bên ngoài đường tròn)
⇒sđMF⏜=2Q^+sđPE⏜
⇒sđMF⏜+sđEF⏜=2(Q^+N^)+(sđPE⏜+sđPM⏜)
⇒sđME⏜(lớn)=2(Q^+N^)+sđME⏜(nhỏ)
Mà sđME⏜(lớn)=360∘−sđME⏜(nhỏ)
⇒360∘−sđME⏜(nhỏ)=2(Q^+N^)+sđME⏜(nhỏ)
⇒sđME⏜(nhỏ)=180∘−(Q^+N^)=180∘−(35∘+45∘)=100∘
Do đó: MFE^=12sđME⏜(nhỏ)=12.100∘=50∘
Vậy chọn (A) 50∘
(A) 60∘; (B) 120∘;
(C) 240∘; (D) Không tính được.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
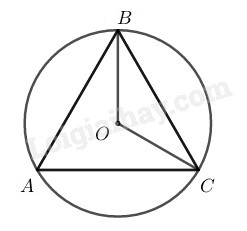
Xét đường tròn (O), ta có: BAC^=12BOC^ (số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung)
Nên BOC^=2BAC^=2.60∘=120∘
Vậy chọn (B) 120∘
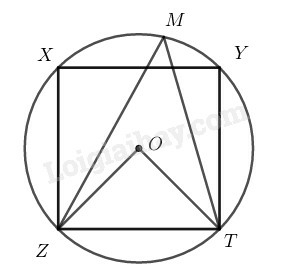
(A) 23∘30′; (B) 45∘;
(C) 90∘; (D) Không tính được.
Phương pháp giải:
Ta sử dụng kiến thức: Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
Vì XYZT là hình vuông nên OT⊥OZ, suy ra ZOT^=900
Xét đường tròn (O), ta có: ZMT^=12ZOT^=12.90∘=45∘ (số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung)
Vậy chọn (B) 45∘
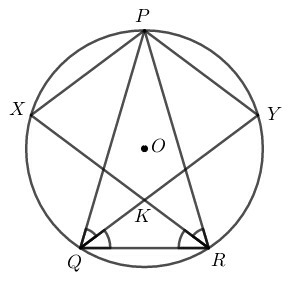
(A) hình thang và không phải là hình bình hành.
(B) hình bình hành và không phải hình thoi.
(C) hình thoi và không phải hình chữ nhật.
(D) hình chữ nhật.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Tứ giác có các góc đối bằng nhau là hình bình hành.
+) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+) Hình chữ nhật là tứ giác có 4 góc vuông.
Lời giải:
Ta có: PQ=PR (gt) nên tam giác PQR cân tại P
Suy ra PQR^=PRQ^
Mà QY,RX lần lượt là tia phân giác của các góc PQR^,PRQ^
Nên PQY^=YQR^=QRX^=XRP^
Suy ra các cung PX,PY,QX,RY bằng nhau (các góc nội tiếp bằng nhau chắn các cung bằng nhau)
Suy ra PRX^=RPY^ (hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Mà hai góc ở vị trí so le trong nên XR//PY
Lại có PQY^=XPQ^ (hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Mà hai góc ở vị trí so le trong nên PX//QY
Suy ra tứ giác PXKY là hình bình hành.
Mà PX=PY (do cung PX bằng cung PY) nên PXKY là hình thoi.
Mặt khác: PXR^≠90∘ (vì PQ không phải đường kính)
Do đó: tứ giác PXKY là hình thoi nhưng không phải hình chữ nhật.
Vậy chọn (C) hình thoi và không phải hình chữ nhật.
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)