tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 8: Giải bài toán bằng cách lập phương trình chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 8: Giải bài toán bằng cách lập phương trình
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Lập phương trình
– Chọn chữ số hàng chục là ẩn và đặt điều kiện: x∈N∗;x≤9.
– Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.
– Lập phương trình biểu thị mối quan hệ giữa các đại lượng .
Bước 2: Giải phương trình nói trên.
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện và kết luận.
Lời giải:
Gọi chữ số hàng chục là x; điều kiện: x∈N∗;x≤9 thì chữ số hàng đơn vị là 10−x.
Giá trị của số đó bằng: 10x+10−x=9x+10
Tích của hai chữ số nhỏ hơn số đã cho là 12, ta có phương trình:
x(10−x)=9x+10−12⇔10x−x2=9x−2⇔x2−x−2=0
Phương trình trên có: a−b+c=1−(−1)+(−2)=1+1−2=0
Phương trình có hai nghiệm x1=−1;x2=−−21=2
Vì x∈N∗ nên x1=−1 không thỏa mãn điều kiện bài toán.
Vậy chữ số hàng chục là 2, chữ số hàng đơn vị là 10−2=8.
Vậy số cần tìm là 28.
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Lập phương trình
– Gọi số dãy ghế ban đầu của phòng họp là x (dãy); điều kiện: x∈N∗.
– Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.
– Lập phương trình biểu thị mối quan hệ giữa các đại lượng .
Bước 2: Giải phương trình nói trên.
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện và kết luận.
Lời giải:
Gọi số dãy ghế ban đầu của phòng họp là x (dãy); điều kiện: x∈N∗.
Số ghế ngồi trong một dãy là 360x (ghế).
Số dãy ghế sau khi tăng thêm là x+1 (dãy)
Số ghế trong một dãy sau khi tăng là 400x+1 (ghế)
Theo bài ra mỗi dãy tăng 1 ghế ta có phương trình:
400x+1−360x=1
⇒400x−360(x+1)=x(x+1)
⇔400x−360x−360=x2+x
⇔x2−39x+360=0
Δ=(−39)2−4.1.360=1521−1440=81>0
Δ=81=9
Phương trình có hai nghiệm phân biệt:
x1=39+92.1=482=24 (thỏa mãn)
x2=39−92.1=302=15 (thỏa mãn)
Vậy số dãy ghế ban đầu là 24 dãy hoặc 15 dãy.
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi trọng tải của xe nhỏ là x (tấn); điều kiện: x>0
Thì trọng tải của xe lớn là (x+0,5) (tấn)
Số lượng xe lớn dự định để chở là: 15x+0,5 (xe)
Số lượng xe nhỏ chở hết 15 tấn là: 15x (xe)
Vì công ty phải dùng một số lượng xe nhỏ nhiều hơn số xe dự định là 1 xe nên ta có phương trình:
15x−15x+0,5=1
⇒15(x+0,5)−15x=x(x+0,5)⇔15x+7,5−15x=x2+0,5x⇔x2+0,5x−7,5=0Δ=12−4.2.(−15)=1+120=121>0Δ=121=11×1=−1+112.2=104=2,5×2=−1−112.2=−124=−3
x2=−3<0 không thỏa mãn điều kiện bài toán: loại
Vậy trọng tải của 1 xe nhỏ là 2,5 tấn.
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi thời gian quy định hoàn thành công việc là x (ngày); điều kiện: x>4
Năng suất quy định là: 450x(m3)
4 ngày trước thời hạn quy định tổ máy sản xuất được là:
450.96100=432(m3)
Thời gian làm được 96% công việc là: x−4 (ngày)
Năng suất thực tế làm là: 432x−4(m3)
Vì thực tế đã tăng năng suất mỗi ngày 4,5m3 nên ta có phương trình:
432x−4−450x=4,5⇒432x−450(x−4)=4,5x(x−4)⇔432x−450x+1800=4,5×2−18x⇔4,5×2−1800=0⇔x2−400=0⇔x2=400⇒x=20hoặcx=−20
Giá trị: x=−20<4 không thỏa mãn điều kiện bài toán: loại
Vậy thời gian quy định là 20 ngày.
Phương pháp giải:
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi khối lượng riêng của chất lỏng thứ hai là x (g/cm3); điều kiện:x>0
Thì khối lượng riêng của chất lỏng thứ nhất là (x+0,2) g/cm3
Thể tích của chất lỏng thứ nhất là: 8x+0,2 g/cm3
Thể tích của chất lỏng thứ hai là: 6x(cm3)
Thể tích của hỗn hợp là: 8+60,7=140,7=20(cm3)
Ta có phương trình:
8x+0,2+6x=20⇒8x+6(x+0,2)=20x(x+0,2)⇔8x+6x+1,2=20×2+4x⇔20×2−10x−1,2=0Δ′=(−5)2−10.(−1,2)=25+24=49>0Δ′=49=7×1=5+720=1220=0,6×2=5−720=−0,1
x2=−0,1<0 không thỏa mãn điều kiện bài toán: loại
Vậy khối lượng riêng của chất lỏng thứ hai là 0,6 (g/cm3)
Khối lượng riêng của chất lỏng thứ nhất là 0,6+0,2=0,8 (g/cm3)
Phương pháp giải:
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi vận tốc lúc về là x(km/h); điều kiện: x>0
Thì vận tốc lúc đi là: (x+10)(km/h)
Thời gian lúc đi là: 150x+10 (giờ)
Thời gian lúc về là: 150x (giờ)
Đổi 3 giờ 15 phút =134 giờ.
Vì tổng thời gian hết tất cả 10 giờ nên ta có phương trình:
150x+10+134+150x=10⇔150x+10+150x=10−134⇔150x+10+150x=274⇒600x+600(x+10)=27x(x+10)⇔600x+600x+6000=27×2+270x⇔27×2−930x−6000=0⇔9×2−310x−2000=0Δ′=(−155)2−9.(−2000)=42025>0Δ′=42025=205×1=155+2059=40×2=155−2059=−509
x2=−509<0 không thỏa mãn điều kiện: loại
Vận tốc ô tô lúc về là 40km/h.
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi vận tốc của máy bay cánh quạt là x(km/h); điều kiện: x>0
Thì vận tốc của máy bay phản lực là (x+300) (km/h)
Thời gian máy bay cánh quạt bay là: 600x (giờ)
Thời gian máy bay phản lực bay là: 600x+300 (giờ)
Máy bay phản lực bay sau 10 phút và đến trước 10 phút nên thời gian máy bay phản lực bay ít hơn máy bay cánh quạt là:
10 phút + 10 phút = 20 phút = 13 giờ
Ta có phương trình:
600x−600x+300=13⇒3.600(x+300)−3.600x=x(x+300)⇔1800x+540000−1800x=x2+300x⇔x2+300x−540000=0Δ′=1502−1.(−540000)=562500>0Δ′=562500=750×1=−150+7501=600×2=−150−7501=−900
x2=−900<0 không thỏa mãn điều kiện: loại
Vậy: vận tốc máy bay cánh quạt là 600km/h
Vận tốc của máy bay phản lực là 600+300=900km/h.
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi vận tốc xe thứ nhất là x(km/h); điều kiện: 0<x<90
Vì sau 1 giờ hai xe gặp nhau, vậy quãng đường hai xe đi được trong một giờ là 90km tức tổng vận tốc của hai xe là 90km/h nên vận tốc của xe thứ hai đi là 90–x(km/h)
Quãng đường xe thứ nhất tiếp tục đi là: 90–x(km)
Thời gian xe thứ nhất đi đoạn đường còn lại là 90−xx giờ
Quãng đường xe thứ hai tiếp tục đi là x(km)
Thời gian xe thứ hai đi đoạn còn lại là x90−x giờ
Xe thứ hai đến Hà Nội trước xe thứ nhất đến Nam Định là 27 phút bằng 920 giờ.
Ta có phương trình:
90−xx−x90−x=920⇒20(90−x)2−20×2=9x(90−x)⇔20(8100−180x+x2)−20×2=810x−9×2⇔162000−3600x+20×2−20×2−810x+9×2=0⇔9×2−4410x+162000=0⇔x2−490x+18000=0Δ′=(−245)2−1.18000=42025>0Δ′=42025=205×1=245+2051=450×2=245−2051=40
x2=450>90 không thỏa mãn điều kiện: loại.
Vậy: vận tốc xe thứ nhất là 40km/h
Vận tốc xe thứ hai là 90−40=50 km/h
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi vận tốc thuyền khi đi trên hồ là x(km/h); điều kiện: x>3
Vận tốc khi đi xuôi dòng trên sông là x+3(km/h)
Vận tốc khi đi ngược dòng trên sông là x–3(km/h)
Thời gian đi xuôi dòng bằng 30x+3 giờ
Thời gian đi ngược dòng bằng 28x−3 giờ
Thời gian đi trên hồ lúc nước yên lặng bằng 59,5x giờ
Ta có phương trình:
30x+3+28x−3=59,5x⇒60x(x−3)+56x(x+3)=119(x+3)(x−3)⇔60×2−180x+56×2+168x=119×2−1071⇔3×2+12x−1071=0⇔x2+4x−357=0Δ′=22−(−357)=361>0Δ′=361=19×1=−2+191=17×2=−2−191=−21
x2=−21<3 không thỏa mãn điều kiện: loại.
Vậy vận tốc thuyền đi trên hồ yên lặng là 17km/h
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi vận tốc của bè gỗ là x(km/h); điều kiện: x>0
Thì vận tốc của xuồng máy là x+12 (km/h)
Thời gian bè từ lúc trôi đến lúc gặp xuồng máy là 20x giờ
Thời gian xuồng máy lúc đi đến lúc gặp bè là 20x+12 giờ
Bè gỗ trôi trước xuồng máy 5 giờ 20 phút bằng 513 giờ = 163 giờ
Ta có phương trình:
20x−20x+12=163⇒60(x+12)−60x=16x(x+12)⇔60x+720−60x=16×2+192x⇔16×2+192x−720=0⇔x2+12x−45=0Δ′=62−1(−45)=36+45=81>0Δ′=81=9×1=−6+91=3×2=−6−91=−15
x2=−15<0 không thỏa mãn điều kiện: loại.
Vậy vận tốc của bè gỗ trôi là 3km/h
Phương pháp giải:
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Đổi 2 giờ 55 phút =3512 giờ.
Gọi thời gian chảy riêng đầy bể của vòi thứ nhất là x giờ
Điều kiện: x>3512
Thì thời gian chảy riêng đầy bể của vòi thứ hai là x+2 giờ
Trong một giờ vòi thứ nhất chảy được 1x bể
Trong một giờ vòi thứ hai chảy được 1x+2 bể
Trong một giờ cả hai vòi chảy được 1:3512=1235 bể
Ta có phương trình:
1x+1x+2=1235⇒35(x+2)+35x=12x(x+2)⇔35x+70+35x=12×2+24x⇔12×2−46x−70=0⇔6×2−23x−35=0Δ=(−23)2−4.6.(−35)=1369>0Δ=1369=37×1=23+372.6=5×2=23−372.6=−76
x2=−76<21112 không thỏa mãn điều kiện: loại.
Vậy: vòi thứ nhất chảy riêng đầy bể sau 5 giờ
Vòi thứ hai chảy riêng đầy bể sau 5+2=7 giờ
Phương pháp giải:
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi thời gian đội thứ nhất làm riêng xong nửa công việc là x ngày
Điều kiện: 6<x<25
Thì thời gian làm riêng xong nửa công việc của đội thứ hai là 25–x ngày
Trong 1 ngày đội thứ nhất làm được 12x công việc
Trong một ngày đội thứ hai làm được 12(25−x) công việc
Trong một ngày cả hai đội làm được 112 công việc
Ta có phương trình:
12x+12(25−x)=112⇒24(25−x)+24x=4x(25−x)⇔600−24x+24x=100x−4×2⇔4×2−100x+600=0⇔x2−25x+150=0Δ=(−25)2−4.150=25>0Δ=25=5×1=25+52.1=15×2=25−52.1=10
Cả hai giá trị thỏa mãn điều kiện bài toán
Vậy đội thứ nhất làm riêng xong công việc trong 2.15=30 ngày thì đội thứ hai làm riêng xong trong 2.10=20 ngày.
Hoặc đội thứ nhất làm riêng xong công việc trong 2.10=20 ngày thì đội thứ hai làm riêng xong trong 2.15=30 ngày.
Phương pháp giải:
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
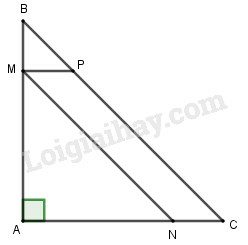
Gọi độ dài đoạn MA=x(cm); điều kiện 0<x<12
Vì ∆ABC vuông cân tại A nên tam giác BMP vuông cân tại M
⇒MP=MB=AB–AM=12–x(cm)
Diện tích hình bình hành MNCP bằng MP.MA
Suy ra: MP.MA=(12–x)x
Ta có phương trình:
(12−x)x=32⇒x2−12x+32=0Δ′=(−6)2−1.32=36−32=4>0Δ′=4=2×1=6+21=8×2=6−21=4
Cả hai giá trị x1=8 và x2=4 thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A là 8cm hoặc 4cm thì diện tích hình bình hành MNCP bằng 32cm2.
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi chu vi của bánh trước là x(m), điều kiện: x>0
Chu vi của bánh sau là x+1,5(m)
Số vòng quay của bánh trước là 100x vòng
Số vòng quay của bánh sau là 100x+1,5 vòng
Vì đi trên đoạn đường dài 100m thì bánh trước quay nhiều hơn bánh sau 15 vòng nên ta có phương trình:
100x−100x+1,5=15⇒100(x+1,5)−100x=15x(x+1,5)⇔100x+150−100x=15×2+22,5x⇔15×2+22,5x−150=0⇔2×2+3x−20=0Δ=32−4.2.(−20)=9+160=169>0Δ=169=13×1=−3+132.2=2,5×2=−3−132.2=−4
x2=−4<0 không thỏa mãn điều kiện: loại.
Vậy chu vi bánh xe trước bằng 2,5m
Chu vi bánh xe sau bằng 2,5+1,5=4m
Một đàn khỉ chia thành hai nhóm.
Nhóm chơi đùa vui vẻ ngoài trời
Bằng bình phương một phần tám của đàn.
Mười hai con nhảy nhót trên cây.
Không khí tươi vui sưởi ấm nơi này.
Hỏi có tất cả bao nhiêu con khỉ?
Phương pháp giải:
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi số khỉ của đàn là x (con)
Điều kiện: x∈N∗ và x⋮8
Nhóm chơi đùa ngoài trời có (x8)2 con
Nhóm nhảy nhót trên cây là 12 con
Ta có phương trình:
x=(x8)2+12⇔x=x264+12⇔x2−64x+768=0Δ′=(−32)2−1.768=1024−768=256>0Δ′=256=16×1=32+161=48×2=32−161=16
Cả hai giá trị x1=48 và x2=16 thỏa mãn điều kiện bài toán
Vậy đàn khỉ có 48 con hoặc 16 con
Hai nông dân đem 100 quả trứng ra chợ bán. Số trứng của hai người không bằng nhau, nhưng hai người bán được số tiền bằng nhau. Một người nói với người kia: “Nếu số trứng của tôi bằng số trứng của anh thì tôi bán được 15 đồng”. Người kia nói: “Nếu số trứng của tôi bằng số trứng của anh thì tôi chỉ bán được 623 đồng thôi”. Hỏi mỗi người có bao nhiêu trứng?
Phương pháp giải:
* Các bước giải bài toán bằng cách lập phương trình
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
Lời giải:
Gọi số trứng của người thứ nhất là x (quả)
Điều kiện: x∈N∗ và x<100
Thì số trứng của người thứ hai là 100–x (quả)
Giá tiền một quả trứng của người thứ nhất: 15100−x đồng
Đổi 623=203
Giá tiền một quả trứng của người thứ hai 203x đồng
Số tiền người thứ nhất thu được là 15100−x.x=15×100−x đồng
Số tiền người thứ hai thu được là: 203x.(100−x)=20(100−x)3x đồng
Vì hai người bán được số tiền bằng nhau nên ta có phương trình:
15×100−x=20(100−x)3x⇒45×2=20(100−x)2⇔45×2=20(10000−200x+x2)⇔45×2=200000−4000x+20×2⇔25×2+4000x−200000=0⇔x2+160x−8000=0Δ′=802−1.(−8000)=6400+8000=14400>0Δ′=14400=120×1=−80+1201=40×2=−80−1201=−200
Giá trị x2=−200∉N∗ không thỏa mãn điều kiện: loại.
Vậy: số trứng người thứ nhất là 40 quả
Số trứng người thứ hai là 60 quả.
