SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 

Bài 44 trang 107 SBT Toán 9 tập 2: Vẽ hình vuông ABCD tâm O rồi vẽ tam giác đều có một đỉnh là A và nhận O làm tâm. Nêu cách vẽ.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Hình vuông là có hai đường chéo bằng nhau, cắt nhau tại trung điểm mỗi đường, và hai đường chéo vuông góc với nhau.

+) Tam giác đều có các cạnh, các góc bằng nhau bằng 60∘.

+) Bất kì đa giác nào cũng có một và chỉ một đường tròn ngoại tiếp.

Lời giải:

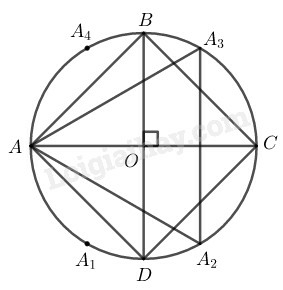
Cách vẽ:  

− Vẽ đường tròn (O;R)

− Kẻ 2 đường kính AC⊥BD

− Nối AB,BC,CD,DA ta được tứ giác ABCD là hình vuông nội tiếp trong đường tròn (O;R)

− Từ A đặt liên tiếp các cung bằng nhau có dây tương ứng bằng bán kính R là: 

AA1⏜, A1A2⏜, A2C⏜, CA3⏜, A3A4⏜

Nối AA2,A2A3,A3A, ta có ∆AA2A3, là tam giác đều nhận O làm tâm.

Chứng minh:

Vì các cung AA1⏜, A1A2⏜, A2C⏜, CA3⏜, A3A4⏜ bằng nhau nên ta có:

AA2⏜=A2A3⏜=A3A⏜

Suy ra AA2=A2A3=A3A nên tam giác AA2A3 là tam giác đều

Theo cách vẽ ta có O là tâm đường tròn ngoại tiếp tam giác AA2A3

Vậy tam giác AA2A3 thỏa mãn đề bài. 

Bài 45 trang 107 SBT Toán 9 tập 2: Vẽ đường tròn tâm O bán kính R=2cm rồi vẽ hình tám cạnh đều nội tiếp đường tròn (O;2cm). Nêu cách vẽ.

Ta sử dụng kiến thức:

+) Tất cả các đỉnh của đa giác đều đều nằm trên một đường tròn. Tất cả các đa giác đều đều có một đường tròn ngoại tiếp.

Lời giải:

Cách vẽ:

− Vẽ đường tròn (0;2cm) 

− Vẽ đường kính AC⊥BD

− Nối AB,BC,CD,DA ta có hình vuông ABCD nội tiếp đường tròn (0;2cm)

− Kẻ đường kính EF⊥AD; đường kính GH⊥AB

Nối AE,ED,DG,GC,CF,FB,BH,HA ta có đa giác AEDGCFBH là đa giác đều 8 cạnh nội tiếp trong đường tròn (0;2cm).

Bài 46 trang 107 SBT Toán 9 tập 2: Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó.

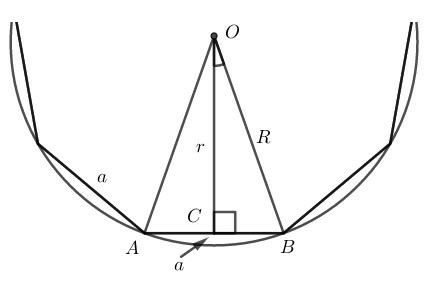
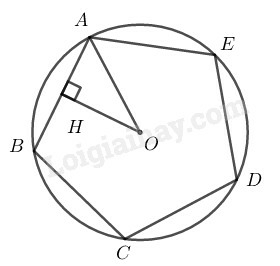
Hướng dẫn:

Tính COB^ rồi tính sin⁡COB^ và tan⁡COB^, từ đây tính được R và r (h.4).

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều n cạnh bằng 360∘n.

Lời giải:

Giả sử một đa giác đều n cạnh có độ dài một cạnh là a. Gọi R là bán kính đường tròn ngoại tiếp, r bán kính đường tròn nội tiếp. 

⇒OB=R;OC=r

AOB^=360∘n

⇒COB^=360∘n:2=180∘n

Trong ∆OCB ta có: OCB^=90∘

Nên sin⁡COB^=CBOB=a2R=a2R

⇒2R=asin180∘n

⇒R=a2sin180∘n

Xét tam giác OCB vuông tại C, ta có:

tan⁡COB^=CBOC=a2r=a2r

⇒2r=atan180∘n

⇒r=a2tan180∘n

Bài 47 trang 108 SBT Toán 9 tập 2:

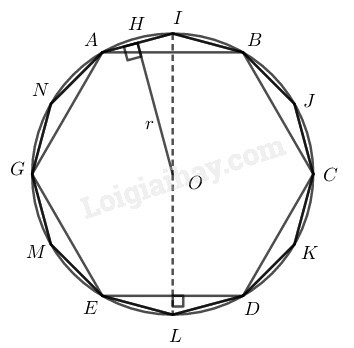
a) Vẽ một lục giác đều ABCDEG nội tiếp đường tròn bán kính 2cm rồi vẽ hình 12 cạnh đều AIBJCKDLEMGN nội tiếp đường tròn đó. Nêu cách vẽ.

b) Tính độ dài cạnh AI.

c) Tính bán kính r của đường tròn nội tiếp hình AIBJCKDLEMGN.

Hướng dẫn. Áp dụng các công thức ở bài 46.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều n cạnh bằng 360∘n.

Lời giải:

a) Cách vẽ:

− Vẽ đường tròn (0;2cm) 

− Từ điểm A trên đường tròn (0;2cm) đặt liên tiếp các cung bằng nhau có dây căng cung 2cm.

AB⏜ =BC⏜ =CD⏜ =DE⏜ =EG⏜

Nối AB,BC,CD,DE,EG,GA ta có lục giác đều ABCDEG nội tiếp trong đường tròn (0;2cm).

− Kẻ đường kính vuông góc với AB và DE cắt đường tròn tại I và L.

Ta có: AI⏜=IB⏜; LD⏜=LE⏜

− Kẻ đường kính vuông góc với BC và EG cắt đường tròn tại J và M.

BJ⏜=JC⏜; ME⏜=MG⏜

− Kẻ đường kính vuông góc với CD và AG cắt đường tròn tại N và K.

KC⏜=KD⏜; NA⏜=NG⏜

Nối AI,IB,BJ,JC,CK,KD,DL, LE, EM, MG, GN, NA

Ta có đa giác đều 12 cạnh AIBJCKDLEMGN.

b) AI là cạnh của đa giác đều 12 cạnh.

Kẻ OH⊥AI

IOH^=180∘12=15∘

Xét tam giác vuông IOH có: OI=HIsin⁡IOH^

⇒OI=AI2sin⁡IOH^

⇒AI=OI.2sin⁡IOH^

AI=2.2sin15∘≈1,04(cm)

c) OH=r bán kính đường tròn nội tiếp đa giác đều 12 cạnh.

Trong tam giác vuông OHI ta có OH=OI.cosHOI^=2.cos15∘≈1,93(cm)

Bài 48 trang 108 SBT Toán 9 tập 2:

a) Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính 3cm.

b) Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính 3cm. 

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều n cạnh bằng 360∘n.

Lời giải:

a) Kẻ OH⊥AB, ta có: HA=HB=12AB,OA=R=3cm

Vì ABCDE là ngũ giác đều nên: BOA^=360∘5=72∘ 

Suy ra HOA^=BOA^2=72∘5=36∘ 

Trong tam giác vuông OHA vuông tại H ta có: 

AH=OA.sin⁡HOA^

⇒AB=2.AH=2OA.sin⁡HOA^=2.3.sin⁡36∘≈3,522 (cm)

b) Từ giả thiết suy ra OH=r=3cm

Trong tam giác vuông OHA vuông tại H ta có:

 AH=OH.tan⁡HOA^ ⇒AB=2.AH=2.OH.tan⁡HOA^=2.3.tan⁡36∘≈4,356 (cm)

Bài 49 trang 108 SBT Toán 9 tập 2: Tính cạnh của hình tám cạnh đều theo bán kính R của đường tròn ngoại tiếp.

Hướng dẫn:

Cách 1: áp dụng công thức a=2Rsin180∘n

Cách 2: tính trực tiếp.

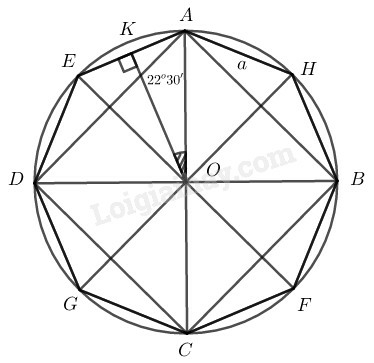
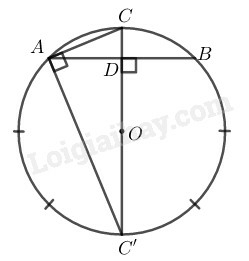
Vẽ dây AB là cạnh của một hình vuông nội tiếp đường tròn (O), gọi C là điểm chính giữa của cung nhỏ AB. Khi đó CA là cạnh của hình tám cạnh đều nội tiếp. Hãy tính CA trong tam giác vuông CAC′.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu của cạnh góc vuông đó trên cạnh huyền.

Lời giải:

Cách 1: Áp dụng công thức a=2Rsin⁡180∘n, ta có:

a=2Rsin⁡22∘30′≈0,765R 

Cách 2:

AC là cạnh của đa giác đều 8 cạnh.

Nên sđAC⏜=18.3600=450

Do đó AC′C^=sđAC⏜2=22030′ (tính chất góc nội tiếp)

Trong tam giác vuông CAC′, ta có:

sin⁡AC′C^=ACCC′ 

⇒AC=CC′.sin⁡AC′C^=2R.sin⁡22030′≈0,765R

Bài 50 trang 108 SBT Toán 9 tập 2: Trong đường tròn (O;R) cho một dây AB bằng cạnh hình vuông nội tiếp và dây BC bằng cạnh tam giác đều nội tiếp (điểm C và điểm A ở cùng một phía đối với BO). Tính các cạnh của tam giác ABC và đường cao AH của nó theo R.

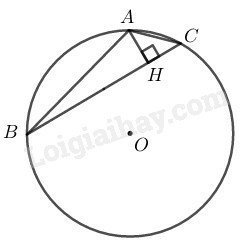
Ta sử dụng kiến thức:

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.

Lời giải:

Dây AB bằng cạnh hình vuông nội tiếp đường tròn (O;R) nên AB=R2 và cung AB⏜ nhỏ có  sđAB⏜=3600:4=90∘.

Dây BC bằng cạnh hình tam giác đều nội tiếp đường tròn (O;R) nên BC=R3 và cung nhỏ BC⏜ có  sđBC⏜=3600:3=120∘.

⇒sđAC⏜=sđBC⏜−sđAB⏜ =120∘−90∘=30∘

⇒ABC^=12sđAC⏜=15∘ (tính chất góc nội tiếp)

Trong ∆AHB có AHB^=90∘

⇒AH=AB.sin⁡ABH^=R2.sin⁡15∘≈0,36R

Trong ∆AHC có AHC^=90∘

ACB^=12 sđ AB⏜=45∘ (tính chất góc nội tiếp)

AC=AHsin⁡ACH^=AHsin⁡45∘≈0,36Rsin⁡45∘≈0,51R

Bài 51 trang 108 SBT Toán 9 tập 2: Cho ngũ giác đều ABCDE. Gọi I là giao điểm của AD và BE. Chứng minh DI2=AI.AD

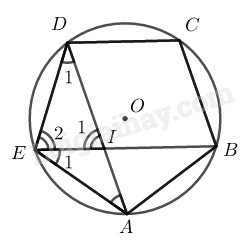
Ta sử dụng kiến thức:

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều n cạnh bằng 360∘n.

+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Lời giải:

Vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE 

sđAB⏜=sđBC⏜=sđCD⏜=sđDE⏜=sđAE⏜=360∘5=72∘(1)

E1^=12sđAB⏜ (tính chất góc nội tiếp)   (2)

D1^=12sđAE⏜ (tính chất góc nội tiếp)   (3)

Từ (1), (2) và (3) suy ra: E1^=D1^

Xét ∆AIE và ∆AED:

+) E1^=D1^ (chứng minh trên)

+) A^ chung

Suy ra: ∆AIE đồng dạng ∆AED(g.g)

Do đó: AIAE=AEAD

⇒ AE2=AI.AD(∗)

Lại có: E2^=12sđBCD⏜ (tính chất góc nội tiếp) hay E2^=12(sđBC⏜+sđCD⏜) (4)

I1^=12(sđDE⏜+sđAB⏜) (tính chất góc có đỉnh ở trong đường tròn)  (5)

Từ (1), (4) và (5) suy ra: E2^=I1^

⇒ ∆DEI cân tại D ⇒DE=DI

          DE=AE(gt)

Suy ra:DI=AE(∗∗)

Từ (∗) và (∗∗) suy ra:DI2=AI.AD

Bài tập bổ sung (trang 109 SBT Toán 9)

Bài 8.1 trang 109 SBT Toán 9 tập 2: Mỗi câu sau đây đúng hay sai?

a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp.

b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp.

c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.

d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.

e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.

f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.

g) Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn.

h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.

i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

Lời giải:

Câu a: Đúng 

Câu b: Sai

Câu c: Sai vì giao ba đường trung trực là tâm đường tròn ngoại tiếp tam giác.

Câu d: Đúng

Câu e: Đúng

Câu f: Sai vì giao ba đường phân giác là tâm đường tròn nội tiếp tam giác.

Câu g: Đúng

Câu h: Đúng

Câu i: Sai vì nó còn có thể là đường tròn bàng tiếp tam giác.

Bài 8.2 trang 109 SBT Toán 9 tập 2: Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA, MB với đường tròn (O). Qua điểm M kẻ cát tuyến MCD với đường tròn (O) (tức là đường thẳng đi qua điểm M và cắt đường tròn tại hai điểm C,D). Gọi I là trung điểm của dây CD. Khi đó MAOIB có là ngũ giác nội tiếp hay không?

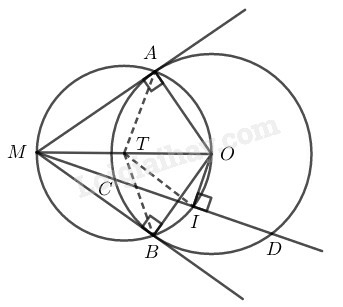
Ta sử dụng kiến thức:

+) Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Nếu các đỉnh của đa giác cùng nhìn một cạnh dưới góc vuông thì đa giác đó nội tiếp đường tròn.