tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 3: Góc nội tiếp chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 3: Góc nội tiếp
Phương pháp giải:
+) Vẽ hình: dùng thước thẳng và compa để vẽ hình
+) Chứng minh: Sử dụng dấu hiệu nhận biết hình bình hành và hình vuông
Dấu hiệu nhận biết hình bình hành: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Dấu hiệu nhận biết hình vuông: Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
Lời giải:
Cách vẽ:
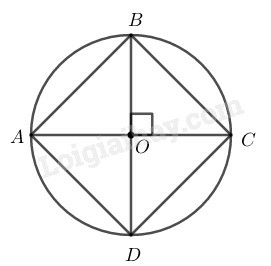
– Vẽ đường tròn (O;1,5cm)
– Vẽ 2 đường kính AC và BD vuông góc với nhau.
– Nối AB,BC,CD,DA ta có tứ giác ABCD là hình vuông có 4 đỉnh nằm trên cung tròn (O;1,5cm).
Chứng minh:
Theo cách vẽ ta có: OA=OC=R,OB=OD=R nên tứ giác ABCD là hình bình hành
Lại có: AC=BD=2R nên hình bình hành ABCD là hình chữ nhật.
Mặt khác: BD⊥AC nên hình chữ nhật ABCD là hình vuông.
Vậy tứ giác ABCD là hình vuông.
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
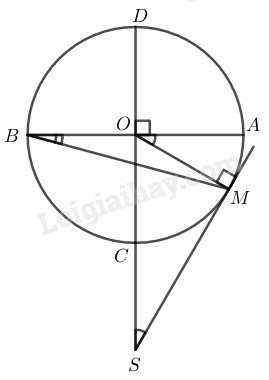
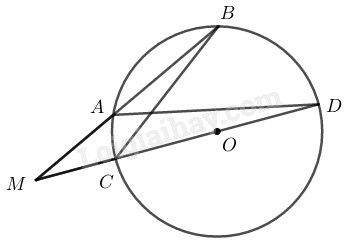
Xét đường tròn (O) có SM⊥OM (tính chất tiếp tuyến)
⇒ΔOMS vuông tại M
Nên MSO^+MOS^=90o
Lại có: AB⊥CD (gt)
⇒MOS^+MOA^=90o
Suy ra: MSO^=MOA^ hay MSD^=MOA^ (1)
Mà MOA^=2MBA^ (góc ở tâm và góc nội tiếp cùng chắn cung AM⏜) (2)
Từ (1) và (2) suy ra: MSD^=2MBA^
Phương pháp giải:
Ta sử dụng kiến thức:
+) Với hai cung nhỏ trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+) Trong một đường tròn, góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
Lời giải:
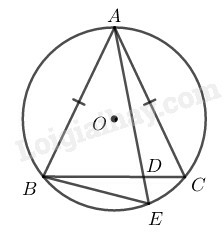
Vì AB=AC(gt)
Nên AB⏜=AC⏜ (hai dây bằng nhau căng 2 cung bằng nhau)
⇒ABC^=AEB^ (2 góc nội tiếp chắn 2 cung bằng nhau)
Xét ∆ABD và ∆ABE:
+) A^ chung
+) ABD^=ABC^=AEB^ (chứng minh trên)
Suy ra: ∆ABD đồng dạng ∆AEB (g-g)
⇒AEAB=ABAD⇒AB2=AD.AE.
Phương pháp giải:
sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
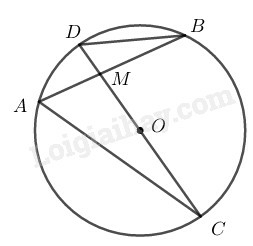
* Trường hợp M ở bên trong đường tròn (O)
Kẻ cát tuyến MAB bất kì của (O) và đường thẳng MO cắt đường tròn (O) tại C và D.
Xét hai ∆MAC và ∆MDB:
+) AMC^=BMD^ (đối đỉnh)
+) A^=D^ (hai góc nội tiếp cùng chắn cung BC⏜)
Suy ra: ∆MAC đồng dạng ∆MDB (g.g)
⇒MAMD=MCMB
⇒MA.MB=MC.MD (1)
Vì M,O cố định suy ra điểm C và D cố định nên độ dài của các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi (2)
Từ (1) và (2) suy ra tích MA.MB không đổi khi cát tuyến MAB thay đổi.
* Trường hợp điểm M ở ngoài đường tròn (O)
Kẻ cát tuyến MAB bất kỳ của (O) và đường thẳng MO cắt đường tròn (O) tại C và D
Xét ∆MAD và ∆MCB:
+) M^ chung
+) B^=D^ (hai góc nội tiếp cùng chắn cung AC⏜)
Suy ra: ∆MAD đồng dạng ∆MCB(g.g)
⇒MCMA=MBMD
⇒MA.MB=MC.MD (3)
Vì M và O cố định suy ra điểm C,D cố định nên độ dài của các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi (4)
Từ (3) và (4) suy ra tích MA.MB không đổi khi cát tuyến MAB thay đổi.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
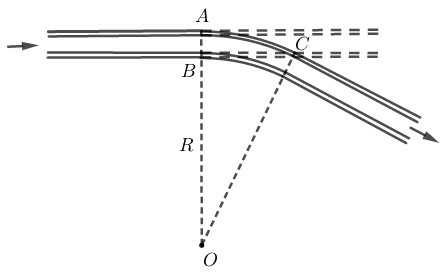
Ta xem hai đoạn đường ray thẳng là tiếp tuyến của hai đoạn đường ray vòng cung.
Điểm B cố định nằm trong đường tròn có cung AC⏜.
Đường thẳng OB cắt đường tròn đó tại A và A′.
A cố định và A′ cố định
B là tiếp điểm cung nhỏ trong nên BC là tiếp tuyến của đường tròn (O;OB)
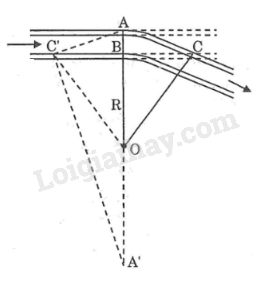
⇒BC⊥OB. Kéo dài BC cắt đường tròn (O;OA) tại C′
⇒BC=BC′ (đường kính vuông góc dây cung)
Xét ∆BAC và ∆BA′C:
+) ABC^=C′BA′^ (đối đỉnh)
+) ACB^=C′A′B^ (2 góc nội tiếp cùng chắn cung AC′⏜)
Suy ra: ∆BAC đồng dạng ∆BC′A′(g.g)
⇒BC′AB=BA′BC
⇒BC.BC′=AB.BA′ mà BC=BC′;BA′=2R–AB
Suy ra: BC2=AB(2R−AB)
(28,4)2≈1,1.(2R−1,1)
⇒2,2R≈806,56+1,21
R≈807,77:2,2=367,2 (m).
a) Hỏi tam giác MBD là tam giác gì?
b) So sánh hai tam giác BDA và BMC.
c) Chứng minh rằng MA=MB+MC.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
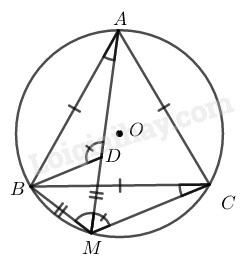
a) MB=MD(gt) ⇒ ∆MBD cân tại M
AMB^=ACB^ (2 góc nội tiếp cùng chắn cung AB⏜)
Mà ACB^=600 (vì ∆ABC đều)
⇒AMB^=600 hay DMB^=600
Vậy ∆MBD đều
b) ∆MBD đều
⇒DBC^+CBM^=DBM^=600 (1)
∆ABC đều ⇒ABD^+DBC^=ABC^=600 (2)
Từ (1) và (2) suy ra: CBM^=ABD^
Xét ∆BDA và ∆BMC:
BA=BC(gt)
ABD^=CBM^ (chứng minh trên)
BD=BM (vì ∆MBD đều)
Suy ra: ∆BDA=∆BMC(c.g.c)
c) ∆BDA=∆BMC (chứng minh trên)
⇒DA=MC
Ta có: MB=MD(gt) mà AM=AD+DM
Suy ra: MA=MB+MC(đpcm)
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải:
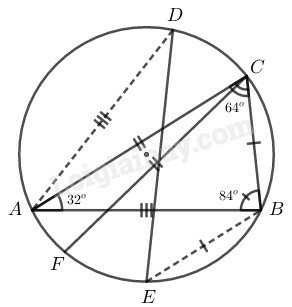
Xét đường tròn (O) có:
A^=12sđBC⏜ (tính chất góc nội tiếp)
⇒sđBC⏜ =2A^=2.32o=64o
Ta có: BC=BE(gt)
⇒sđBC⏜=sđBE⏜=64o
Mà B^=12sđAC⏜ (tính chất góc nội tiếp)
⇒ sđ AC⏜ =2B^=2.84o=168o
Lại có: AC=CF(gt)
⇒sđCF⏜ =sđAC⏜=168o
sđAC⏜+sđAF⏜+sđCF⏜=360o
⇒sđAF⏜ =360o−sđAC⏜−sđCF⏜=360o–168o.2=24o
Trong ∆ABC ta có: A^+B^+C^=180o
⇒ACB^=1800−(A^+B^)
=1800−(32o+84o)=64o
Mà ACB^=12sđAB⏜ (tính chất góc nội tiếp)
⇒sđAB⏜=2ACB^=2.64o=128o
Lại có AD=AB(gt)
⇒sđAD⏜=sđAB⏜=128o
Ta có: FED^=12sđDF⏜ =12(sđAD⏜+sđAF⏜)
=12.(128o+24o)=76o
EDF^=12sđEF⏜ =12(sđAB⏜−sđAF⏜−sđBE⏜)
=12.(128o−24o−64o)=20o
DFE^=180o−(FED^+EDF^)
=1800−(76o+20o)=84o
Ta sử dụng kiến thức:
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
Lời giải:
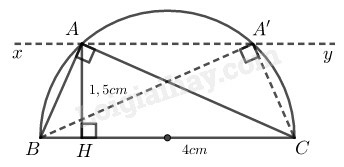
Cách vẽ:
– Vẽ đoạn BC=4cm.
– Vẽ nửa đường tròn đường kính BC
– Vẽ đường thẳng xy nằm trên nửa mặt phẳng chứa nửa đường tròn và xy//BC, cách BC một khoảng bằng 1,5cm.
– Đường thẳng xy cắt nửa đường tròn đường kính BC tại A và A′. Nối AB,AC,A′B,A′C ta có ∆ABC hoặc ∆A′BC cần vẽ.
Chứng minh:
Vì xy cách BC một khoảng 1,5m<BC2=2cm nên đường thẳng xy cắt nửa đường tròn đường kính BC.
Ta lại có ∆ABC nội tiếp trong nửa đường tròn đường kính BC nên BAC^=90o
Có AH⊥BC và AH=1,5cm.
Vậy tam giác ABC hoặc tam giác A′BC thỏa mãn đề bài.
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc kề cạnh đáy bằng nhau.
+) Trong một đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
+) Tứ giác có các cặp góc song song là hình bình hành.
+) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Lời giải:
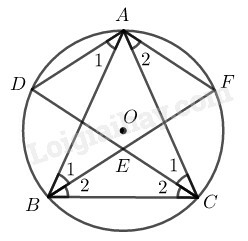
Vì ∆ABC cân tại A
⇒ABC^=ACB^ (tính chất tam giác cân)
Lại có:
BF là tia phân giác của ABC^ (gt)
CD là tia phân giác của ACB^ (gt)
Suy ra: B1^=B2^=C1^=C2^
Suy ra: AD⏜=DB⏜=AF⏜=FC⏜
Từ đó, đường tròn (O) có: A1^=B1^ (hai góc nội tiếp chắn 2 cung bằng nhau BD và AF)
⇒AD//BF (vì có cặp góc so le trong bằng nhau)
Hay AD//EF(1)
Tương tự: A2^=C1^ (hai góc nội tiếp chắn 2 cung bằng nhau)
⇒AF//CD (vì có cặp góc ở vị trí so le trong bằng nhau)
Hay AF//ED(2)
Mà AD⏜=AF⏜ (chứng minh trên)
⇒AD=AF (3)
Từ (1), (2) và (3) suy ra: Tứ giác ADEF là hình thoi
Bài tập bổ sung (trang 103 SBT Toán 9)
(A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó.
(B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
(C) Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau.
(D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn.
(E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
Chọn câu đúng: (E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Các câu (A), (B), (C), (D) đều sai.
a) ADC^ và ABC^ có bằng nhau không? Vì sao?
b) Chứng minh CD song song với AB.
c) Chứng minh AD vuông góc với OC
d) Tính số đo của DAO^.
e) So sánh hai cung BE và CD.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+) Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Trong hình thoi, hai đường chéo vuông góc.
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải:
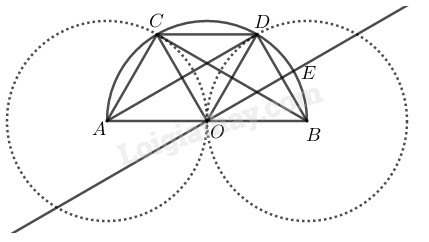
a) Trong đường tròn (O) ta có:
ADC^=ABC^ (2 góc nội tiếp cùng chắn cung AC⏜)
b) ∆ACB nội tiếp trong đường tròn (O) có AB là đường kính nên ∆ABC vuông tại C
⇒CO=OA=12AB (tính chất tam giác vuông)
Mà AC=AO (bán kính đường tròn (A))
Suy ra: AC=AO=OC
⇒∆ACO đều ⇒AOC^=60o
Ta có: ∆ADB nội tiếp trong đường tròn đường kính AB nên ∆ADB vuông tại D
⇒DO=OB=OA=12AB (tính chất tam giác vuông)
BD=BO (bán kính đường tròn (B))
Suy ra: BO=OD=BD
⇒ ∆BOD đều
⇒ODB^=BOD^=60o
Mà AOC^+COD^+BOD^=180o
Suy ra: COD^=60o
Kết hợp với: OC=OD (vì cùng bằng 12AB)
Suy ra: ∆COD đều
⇒ODC^=60o⇒ODC^=BOD^
⇒ CD//AB (vì có cặp góc ở vị trí so le trong bằng nhau)
c) Ta có: ∆AOC đều (chứng minh trên) ⇒OA=AC=OC
∆OCD đều (chứng minh trên) ⇒OC=OD=CD
Suy ra: AC=AO=OD=DC
Vậy: tứ giác AODC là hình thoi. Suy ra AD⊥OC.
d) ∆BOD đều (chứng minh trên) ⇒OBD^=60o hay ABD^=60o
Vì ∆ADB vuông tại D
⇒DAB^+ABD^=90o
⇒DAB^=90o−ABD^=90o−60o=30o
Vậy DAO^=30o
e) OE//AD(gt)
⇒EOB^=DAO^=30o (hai góc đồng vị)
sđBE⏜ =EOB^=300
sđCD⏜ =COD^
mà COD^=60o (chứng minh trên)
sđCD⏜=60o
Suy ra: Số đo cung CD⏜ gấp đôi số đo cung BE⏜.
