tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 3: Bảng lượng giác chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 3: Bảng lượng giác
sin39∘13′; cos52∘18′;
tg13∘20′; cotg10∘17′;
sin45∘; cos45∘.
Phương pháp giải:
Dùng cho bảng lượng giác để tìm các góc.
Lời giải:
sin39∘13′≈0,6323;
cos52∘18′≈0,6115;
tg13∘20′≈0,2370;
cotg10∘17′≈0,5118;
sin45∘≈0,7071;
cos45∘≈0,7071.
a) sinx=0,5446;
b) cosx=0,4444;
c) tgx=1,1111.
Phương pháp giải:
Dùng bảng lượng giác hoặc máy tính bỏ túi tìm góc x.
Lời giải:
a) sinx=0,5446⇒x≈33∘
b) cosx=0,4444⇒x≈63∘37′
c) tgx=1,1111⇒x≈48∘
a) sinx=1,0100;
b) cosx=2,3540;
c) tgx=1,6754?
Phương pháp giải:
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm x.
Lời giải:
a) sinx=1,0100: không có góc nhọn x vì sinx<1
b) cosx=2,3540: không có góc nhọn x vì cosx<1
c) tgx=1,6754⇒x≈59∘10′
Biết:
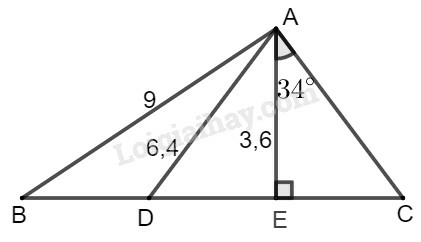
AB=9cm,AC=6,4cm
AN=3,6cm,AND^=90∘,DAN^=34∘
Hãy tính:
a) CN;
b) ABN^;
c) CAN^;
d) AD.
Phương pháp giải:
+) Sử dụng: Định lý Pytago vào tam giác ABC vuông tại A.
AB2+AC2=BC2
+) Sử dụng các tỉ số lượng giác của góc nhọn như sau:
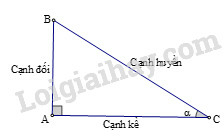
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
a) Áp dụng định lí Pytago vào tam giác vuông ANC, ta có:
AC2=AN2+NC2
⇒NC2=AC2−AN2
⇒NC=AC2−AN2=6,42−3,62=28
⇒NC≈5,2915(cm)
b) Tam giác ANB vuông tại N nên ta có:
sinABN^=ANAB=3,69=0,4
⇒ABN^≈23∘35′
c) Tam giác ANC vuông tại N nên ta có:
cosCAN^=ANAC=3,66,4=916=0,5625⇒CAN^≈55∘46′
d) Tam giác AND vuông tại N nên ta có:
cosNAD^=ANAD⇒AD=ANcosNAD^=3,6cos34∘≈4,3424
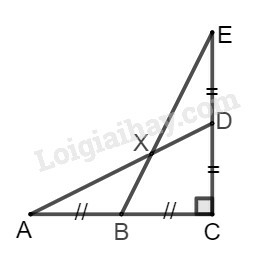
Biết:
ACE^=90∘,AB=BC=CD=DE=2cm.
Hãy tính:
a) AD,BE;
b) DAC^;
c) BXD^.
Phương pháp giải:
+) Định lí Pytago vào tam giác ABC vuông tại A:
AB2+AC2=BC2.
+) Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
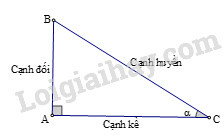
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
a) Ta có:
AC=AB+BC=2+2=4(cm)
Áp dụng định lí Pytago vào tam giác vuông ACD, ta có:
AD2=AC2+CD2=42+22=16+4=20
⇒AD=20=25(cm)
Mặt khác: CE=CD+DE=2+2=4(cm)
Áp dụng định lí Pytago vào tam giác vuông BEC, ta có:
BE2=BC2+CE2=22+42=4+16=20
⇒BE=20=25(cm)
b) Tam giác ACD vuông tại C nên ta có:
tgDAC^=CDAC=24=12
Suy ra: DAC^≈26∘34′
c) Xét tam giác ADC vuông tại C, ta có: CDA^=90∘−CAD^≈90∘−26∘34′=63∘26′
Xét hai tam giác ACD và ECB, ta có:
AC=EC(=4cm)
BC=DC(=2cm)
AD=EB(=25(cm))
Suy ra: ΔACD=ΔECB (c.c.c)
⇒CBE^=CDA^=63∘26′
Trong tứ giác BCDX, ta có:
BXD^=360∘−(C^+CDA^+CBE^)
=360∘−(90∘+63∘26′+63∘26′)=143∘8′.
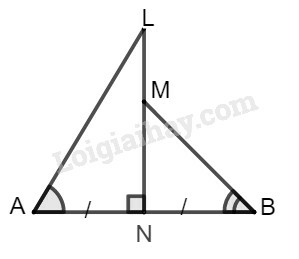
Đoạn thẳng LN vuông góc với đoạn thẳng AB tại trung điểm N của AB; M là một điểm của đoạn thẳng LN và khác với L,N. Hãy so sánh các góc LAN^ và MBN^.
Phương pháp giải:
Cho hình vẽ:
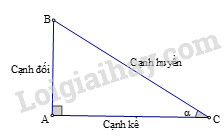
Ta có: tanα=ABAC.
Lời giải:
Tam giác ALN vuông tại N nên ta có:
tgLAN^=NLAN (1)
Tam giác BNM vuông tại N nên ta có:
tgMBN^=NMNB (2)
Mặt khác: AN=NB (gt) (3)
NL>NM (4) (do M thuộc đoạn thẳng LN)
Từ (1), (2), (3) và (4) suy ra: tgMBN^<tgLAN^
Suy ra: MBN^<LAN^ ( vì α tăng thì tgα tăng)
a) sin25∘ và sin70∘;
b) cos40∘ và cos75∘ ;
c) sin38∘ và cos38∘ ;
d) sin50∘ và cos50∘.
Phương pháp giải:
Với 0∘<α<90∘ ta có α tăng thì sinα tăng.
Hay α<β thì sinα<sinβ.
Với 0∘<α<90∘ ta có α tăng thì cosα giảm.
Hay α<β thì cosα>cosβ.
Lời giải:
a)
Với 0∘<α<90∘ ta có α tăng thì sinα tăng
Ta có: 25∘<75∘, suy ra: sin25∘<sin75∘
b)
Với 0∘<α<90∘ ta có α tăng thì cosα giảm
Ta có: 40∘<75∘, suy ra: cos40∘>cos75∘
c)
Ta có: 38∘+52∘=90∘, suy ra: cos38∘=sin52∘
Vì 38∘<52∘ nên sin38∘<sin52∘ hay sin38∘<cos38∘
d)
Ta có: 40∘+50∘=90∘, suy ra: sin50∘=cos40∘
Vì 40∘<50∘ nên cos40∘>cos50∘ hay sin50∘>cos50∘
a) tg50∘28′ và tg63∘;
b) cotg14∘ và cotg35∘12′;
c) tg27∘ và cotg27∘;
d) tg65∘ và cotg65∘.
Phương pháp giải:
Với 0∘<α<90∘ ta có α tăng thì tgα tăng.
Hay α<β thì tgα<tgβ.
Với 0∘<α<90∘ ta có α tăng thì cotgα giảm.
Hay α<β thì cotgα>cotgβ.
Lời giải:
a) Với 0∘<α<90∘ ta có α tăng thì tgα tăng
Ta có: 50∘28′<63∘, suy ra: tg50∘28′<tg63∘
b) Với 0∘<α<90∘ ta có α tăng thì cotgα giảm
Ta có: 14∘<35∘12′, suy ra: cotg14°>cotg35°12′
c) Với 0∘<α<90∘ ta có α tăng thì tgα tăng
Ta có: 27∘+63∘=90∘, suy ra: cotg27∘=tg63∘
Vì 27∘<63∘ nên tg27∘<tg63∘ hay tg27∘<cotg27∘
d) Với 0∘<α<90∘ ta có α tăng thì cotgα giảm
Ta có: 65∘+25∘=90∘ nên tg65°=cotg25°
Vì 25∘<65∘ nên cotg250>cotg650 hay
a) sinx−1
b) 1−cosx
c) sinx−cosx
d) tgx−cotgx
Phương pháp giải:
Với 0∘<α<90∘ ta có α tăng thì sinα tăng.
Hay α<β thì sinα<sinβ.
Với 0∘<α<90∘ ta có α tăng thì cosα giảm.
Hay α<β thì cosα>cosβ.
Với 0∘<α<90∘ ta có α tăng thì tgα tăng.
Hay α<β thì tgα<tgβ.
Với 0∘<α<90∘ ta có α tăng thì cotgα giảm.
Hay α<β thì cotgα>cotgβ.
Lời giải:
a) Ta có: 0∘<α<90∘ với thì sinx<1, suy ra sinx−1<0
b) Ta có: 0∘<α<90∘ với thì cosx<1, suy ra 1−cosx>0
c) Ta có:
* Nếu x=45° thì sinx=cosx, suy ra: sinx−cosx=0
* Nếu x<45° thì cosx=sin(90∘−x)
Vì x<45° nên 90∘−x>45∘ hay x<90∘−x, suy ra: sinx<sin(90∘−x)
Vậy sinx<cosx hay sinx−cosx<0
* Nếu x>45° thì cosx=sin(90∘−x)
Vì x>45° nên 90∘−x<45∘ hay x>90∘−x, suy ra: sinx>sin(90∘−x)
Vậy sinx>cosx hay sinx−cosx>0.
d) Ta có:
* Nếu x=45° thì tgx=cotgx, suy ra: tgx−cotgx=0
* Nếu x<45° thì cotgx=tg(90∘−x)
Vì x<45° nên 90∘−x>45∘ hay x<90∘−x, suy ra: tgx<tg(90∘−x)
Vậy tgx<cotgx hay tgx–cotgx<0.
* Nếu x>45° thì cotgx=tg(90∘−x)
Vì x>45° nên 90∘−x<45∘ hay x>90∘−x, suy ra: tgx>tg(90∘−x)
Vậy tgx>cotgx hay tgx–cotgx>0.
a) tg28∘ và sin28∘;
b) cotg42∘ và cos42∘;
c) cotg73∘ và sin17∘;
d) tg32∘ và cos58∘.
Phương pháp giải:
Với 0∘<α<90∘ ta có α tăng thì sinα tăng.
Hay α<β thì sinα<sinβ.
Với 0∘<α<90∘ ta có α tăng thì cosα giảm.
Hay α<β thì cosα>cosβ.
Với 0∘<α<90∘ ta có α tăng thì tgα tăng.
Hay α<β thì tgα<tgβ.
Với 0∘<α<90∘ ta có α tăng thì cotgα giảm.
Hay α<β thì cotgα>cotgβ.
Lời giải:
a) tg28∘=sin28∘cos28∘=sin28∘.1cos28∘ (1)
Vì 0<cos280<1 nên 1cos28∘>1⇒sin28∘.1cos28∘>sin28∘ (2)
Từ (1) và (2) suy ra: tg28°>sin28°
b) Ta có: cotg42∘=cos42∘sin42∘=cos42∘.1sin42∘ (1)
Vì 0<sin42°<1 nên 1sin42∘>1⇒cos42∘.1sin42∘>cos42∘ (2)
Từ (1) và (2) suy ra: cotg42°>cos42°
c) Ta có: 17°+73°=90° nên cos73∘=sin17∘ (1)
cotg73∘=cos73∘sin73∘=cos73∘.1sin73∘ (2)
Vì 0<sin73°<1 nên 1sin73∘>1 ⇒cos73∘.1sin73∘>cos73∘ (3)
Từ (1), (2) và (3) suy ra: cotg73°>sin17°
d) Ta có: 32°+58°=90° nên sin320=cos58° (1)
tg32∘=sin32∘cos32∘=sin32∘.1cos32∘ (2)
Vì 0<cos32°<1 nên 1cos32∘>1⇒sin32∘.1cos32∘>sin32∘ (3)
Từ (1), (2) và (3) suy ra: tg32°>cos58°
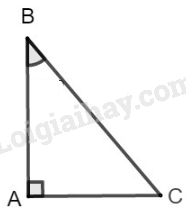
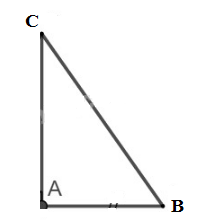
sinB,cosB,tgB,cotgB.
Phương pháp giải:
Sử dụng các tỉ số lượng giác của góc nhọn (hình) như sau:
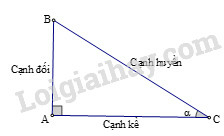
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Định lí Pytago vào tam giác ABC vuông tại A: AB2+AC2=BC2.
Lời giải:
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2
⇒AB2=BC2−AC2=BC2−BC24=3BC24⇒AB=BC32
Vậy: sinB^=ACBC=12BCBC=12
cosB^=ABBC=32BCBC=32
tgB^=ACAB=12BC32BC=33
cotgB^=1tgB=133=3
Phương pháp giải:
Sử dụng tỉ số lượng giác của góc nhọn: sinα=ABBC (hình vẽ)
Định lí Pytago đảo vào tam giác ABC:
Nếu AB2+AC2=BC2 thì tam giác ABC vuông tại A.
Lời giải:
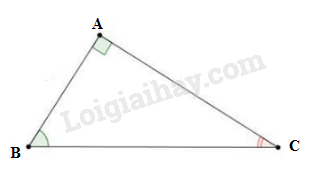
Ta có:
AB=3⇒AB2=32=9
AC=4⇒AC2=42=16
BC=5⇒BC2=52=25
Ta có:
AB2+AC2 =9+16=25=BC2
Suy ra tam giác ABC vuông tại A.
Ta có: sinB^=ACBC=45=0,8⇒B^=53∘8′
C^=90∘−B^=90∘−53∘8′=36∘52′
Sử dụng các tỉ số lượng giác của góc nhọn (hình) như sau:
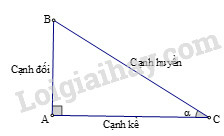
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Định lí Pytago vào tam giác ABC vuông tại A: AB2+AC2=BC2.
Lời giải:
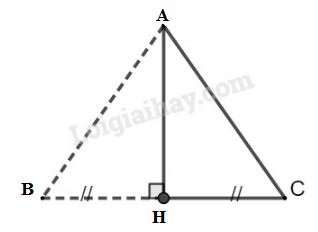
Giả sử tam giác ABC có AB=AC=3cm, BC=4cm.
Kẻ AH⊥BC thì AH cũng là đường trung tuyến của tam giác ABC.
Ta có: BH=12BC=42=2(cm)
Tam giác ABH vuông tại H nên ta có:
cosB^=BHAB=23⇒B^≈48∘11′
Sai số là: 50∘−48∘11′=1∘49′.
Bài tập bổ sung (trang 112,113 SBT Toán 9)
Bài 3.1 trang 112 SBT Toán 9 tập 1: Hãy so sánh:
a) sinα và tanα 0∘<α<90∘ ;
b) cosα và cotgα 0∘<α<90∘
c) sin35∘ và tan38∘
d) cos33∘ và tan61∘.
Phương pháp giải:
Với 0∘<α<90∘ ta có α tăng thì sinα tăng.
Hay α<β thì sinα<sinβ.
Với 0∘<α<90∘ ta có α tăng thì cosα giảm.
Hay α<β thì cosα>cosβ.
Với 0∘<α<90∘ ta có α tăng thì tgα tăng.
Hay α<β thì tgα<tgβ.
Với 0∘<α<90∘ ta có α tăng thì cotgα giảm.
Hay α<β thì cotgα>cotgβ.
Lời giải:
a) Do 0<cosα<1 và sinα>0 nên tanα=sinαcosα>sinα
b) Do 0<sinα<1 và cosα>0 nên cotgα=cosαsinα>cosα
c) Theo a) sin35∘ < tan35∘, mà khi góc lớn lên thì tan cũng lớn lên nên tan35∘ < tan38∘.
Vậy sin35∘ < tan38∘.
d) Theo b) cos33∘ < cotg33∘ mà khi góc lớn lên thì cotang nhỏ đi
Nên cotg33∘<cotg29∘=tan61∘ (vì 29∘+61∘=90∘)
Suy ra cotg33∘ < tan61∘.
a) sin20∘,cos20∘,sin55∘,cos40∘,tan70∘
b) tan70∘,cotg60∘,cotg65∘,tan50∘,sin25∘
Phương pháp giải:
Với 0∘<α<90∘ ta có α tăng thì sinα tăng.
Hay α<β thì sinα<sinβ.
Với 0∘<α<90∘ ta có α tăng thì cosα giảm.
Hay α<β thì cosα>cosβ.
Với 0∘<α<90∘ ta có α tăng thì tgα tăng.
Hay α<β thì tgα<tgβ.
Với 0∘<α<90∘ ta có α tăng thì cotgα giảm.
Hay α<β thì cotgα>cotgβ.
Lời giải:
a) Để ý rằng với các góc nhọn, khi góc lớn lên thì sin của nó lớn lên và chú ý rằng:
cos20∘=sin70∘,cos40∘=sin50∘ và sin70∘<tan 70∘ (do sinα<tgα (theo bài 3.1 trang 112)) nên từ:
Do sin200<sin500<sin550<sin700
Vậy sin20∘<cos40∘<sin55∘<sin70∘<tan70∘
b) Để ý rằng với các góc nhọn, khi góc lớn lên thì tan của góc đó lớn lên.
Ta có: cotg60∘=tan30∘,cotg65∘=tan25∘.
Do sinα<tanα (theo bài 3.1 trang 112) nên sin25∘<tan25∘
Từ đó suy ra: sin25∘<tan25∘<tan30∘<tan50∘<tan70∘
Hay sin25∘<cotg65∘<cotg60∘<tan50∘<tan70∘
a) Hãy biểu thị cạnh góc vuông kia, góc đối diện với cạnh này và cạnh huyền qua b và β.
b) Hãy tìm các giá trị của chúng khi b=10cm, β=50∘ ( làm tròn kết quả đến chữ số thập phân thứ ba).
Phương pháp giải:
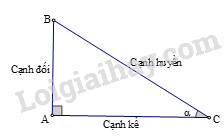
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
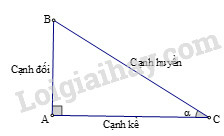
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
Trong tam giác ABC vuông tại A, cạnh AC=b, ABC^=β thì:
a) Theo định nghĩa tỉ số lượng giác của góc nhọn ta có:
tgβ=ACAB=bAB⇒AB=btgβcotgβ=ABAC=ABb⇒AB=b.cotgβ
sinβ=ACBC=bBC⇒BC=bsinβ
Vì tam giác ABC vuông tại A nên ACB^=90∘−β
b) Khi b=10(cm), β=50∘ thì
AB=10tg50∘≈8,391(cm), ACB^=900−500=40∘,BC=10sin50∘≈13,054(cm).
a) Hãy biểu thị cạnh góc vuông kia, góc nhọn kề với cạnh này và cạnh huyền đi qua b và α.
b) Hãy tìm các giá trị của chúng khi b=12cm, a=42∘ ( làm tròn kết quả đến chữ số thập phân thứ ba).
Phương pháp giải:
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:
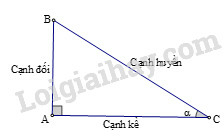
sinα=ABBC;cosα=ACBC;tanα=ABAC;cotα=ACAB.
Lời giải:
Trong tam giác ABC vuông tại A, cạnh AC=b, ACB^=α thì:
a) Theo định nghĩa tỉ số lượng giác của góc nhọn ta có:
tanα=ABAC=ABb⇒AB=c=b.tanαcosα=ACBC=bBC⇒BC=a=bcosα
Vì tam giác ABC vuông tại A nên ABC^=90∘−α
Vậy
AB=c=b.tanα, ABC^=90∘−α,BC=a=bcosα.
b) Khi b=12(cm), a=42∘ thì
c=12.tan42∘≈10,805(cm),
ABC^=900−420=48∘,a=12cos42∘≈16,148(cm).
Related posts
Tài liệu nổi bật
Categories
- Âm Nhạc – Mỹ Thuật Lớp 9 (17)
- Âm nhạc lớp 6 – KNTT (31)
- Âm Nhạc Lớp 7- CTST (23)
- Bài tập Toán 9 (8)
- Chưa phân loại (32)
- Chuyên đề Hóa học 12 (196)
- Chuyên đề Sinh học lớp 12 (61)
- Chuyên đề Toán 9 (50)
- Công Nghệ Lớp 10- CD (58)
- Công Nghệ Lớp 10- KNTT (52)
- Công nghệ Lớp 11 – KNTT (22)
- Công Nghệ Lớp 6 – CTST (15)
- Công Nghệ Lớp 6 – KNTT (16)
- Công Nghệ Lớp 7- CTST (18)
- Công Nghệ Lớp 7- KNTT (19)
- Công nghệ Lớp 8 – CD (21)
- Công nghệ Lớp 8 – CTST (18)
- Công nghệ Lớp 8 – KNTT (7)
- Công Nghệ Lớp 9 (114)
- Đề thi học kì 2 lớp 9 môn Văn (35)
- Địa Lí Lớp 10- CD (99)
- Địa Lí Lớp 10- KNTT (77)
- Địa lí Lớp 11 – CD (31)
- Địa lí Lớp 11 – CTST (23)
- Địa lí Lớp 11 – KNTT (19)
- Địa Lí Lớp 12 (134)
- Địa lí Lớp 6 – CTST (36)
- Địa lí Lớp 6 – KNTT (30)
- Địa Lí Lớp 7- CTST (22)
- Địa Lí Lớp 7- KNTT (19)
- Địa Lí Lớp 9 (290)
- GDCD 12 (28)
- GDCD Lớp 6 – CTST (8)
- GDCD Lớp 6 – KNTT (12)
- GDCD Lớp 9 (94)
- Giải bài tập Địa Lí 12 (12)
- Giải bài tập SGK Toán 12 (8)
- Giải bài tập Sinh học 12 (45)
- Giải SBT Hóa học 12 (71)
- Giải vở BT Văn 9 (122)
- Giáo Dục Công Dân Lớp 7- CTST (12)
- Giáo Dục Công Dân Lớp 7- KNTT (10)
- Giáo dục công dân Lớp 8 – CD (10)
- Giáo dục công dân Lớp 8 – CTST (10)
- Giáo dục công dân Lớp 8 – KNTT (10)
- Giáo Dục Quốc Phòng Lớp 10- CD (12)
- Giáo Dục Quốc Phòng Lớp 10- KNTT (12)
- Hóa Học Lớp 10- CD (30)
- Hóa Học Lớp 10- KNTT (61)
- Hoá Học Lớp 11 – CD (19)
- Hoá học Lớp 11 – CTST (19)
- Hoá học Lớp 11 – KNTT (25)
- Hóa Học Lớp 12 (130)
- Hóa Học Lớp 9 (717)
- Hoạt Động Trải Nghiệm Lớp 10- KNTT (52)
- Hoạt Động Trải Nghiệm Lớp 7- CTST (40)
- Hoạt Động Trải Nghiệm Lớp 7- KNTT (16)
- Hoạt động trải nghiệm Lớp 8 – CD (19)
- Hoạt động trải nghiệm Lớp 8 – CTST (9)
- Hoạt động trải nghiệm Lớp 8 – KNTT (18)
- Khoa học tự nhiên Lớp 6 – CTST (46)
- Khoa học tự nhiên Lớp 6 – KNTT (57)
- Khoa Học Tự Nhiên Lớp 7- CTST (51)
- Khoa học tự nhiên Lớp 8 – CD (51)
- Khoa học tự nhiên Lớp 8 – CTST (33)
- Khoa học tự nhiên Lớp 8 – KNTT (37)
- Kinh Tế & Pháp Luật Lớp 10 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CD (21)
- Kinh tế & Pháp luật Lớp 11 – CTST (11)
- Kinh tế & Pháp luật Lớp 11 – KNTT (11)
- Lịch Sử Lớp 10- CD (34)
- Lịch Sử Lớp 10- CTST (20)
- Lịch Sử Lớp 10- KNTT (42)
- Lịch sử Lớp 11 – CTST (13)
- Lịch sử Lớp 11 – KNTT (13)
- Lịch sử Lớp 6 – CTST (21)
- Lịch sử Lớp 6 – KNTT (22)
- Lịch Sử Lớp 7- CTST (19)
- Lịch sử lớp 7- KNTT (18)
- Lịch Sử Lớp 9 (148)
- Lịch sử và Địa lí Lớp 8 – CTST (40)
- Lịch sử và Địa lí Lớp 8 – KNTT (33)
- Lý thuyết Địa lý 12 (4)
- Lý thuyết Lịch sử lớp 9 (33)
- Lý thuyết Ngữ Văn (83)
- Lý thuyết Ngữ Văn 12 (18)
- Lý thuyết Sinh học 12 (41)
- Mở bài – Kết bài hay (55)
- Mở bài lớp 12 hay (24)
- Nghị luận xã hội (34)
- Ngữ Văn Lớp 10- CD (113)
- Ngữ Văn Lớp 10- CTST (79)
- Ngữ Văn Lớp 10- KNTT (198)
- Ngữ Văn Lớp 11 – CD (51)
- Ngữ văn Lớp 11 – CTST (89)
- Ngữ Văn Lớp 11 – KNTT (107)
- Ngữ Văn Lớp 12 (379)
- Ngữ Văn Lớp 6 – KNTT (293)
- Ngữ Văn Lớp 7- CTST (103)
- Ngữ Văn Lớp 7- KNTT (66)
- Ngữ văn Lớp 8 – CD (48)
- Ngữ văn Lớp 8 – CTST (123)
- Ngữ văn Lớp 8 – KNTT (196)
- Ngữ Văn Lớp 9 (28)
- Phân tích các tác phẩm lớp 12 (12)
- Sinh Học Lớp 10- CD (49)
- Sinh Học Lớp 10- CTST (61)
- Sinh Học Lớp 10- KNTT (71)
- Sinh Học Lớp 11 – CD (16)
- Sinh học Lớp 11 – CTST (18)
- Sinh học Lớp 11 – KNTT (18)
- Sinh Học Lớp 9 (229)
- Soạn Anh 12 mới (86)
- Soạn văn 9 (50)
- SOẠN VĂN 9 BÀI 1 (50)
- SOẠN VĂN 9 BÀI 2 (50)
- Tác giả – Tác phẩm (41)
- Tác giả – Tác phẩm Ngữ Văn 12 (13)
- Thi THPT QG môn Địa lý (12)
- Thi THPT QG môn Sinh (8)
- Tiếng Anh Lớp 10 Friends Global (57)
- Tiếng Anh Lớp 10 Global Success (604)
- Tiếng Anh Lớp 10 iLearn Smart World (98)
- Tiếng anh Lớp 11 Friends Global (171)
- Tiếng anh Lớp 11 Global Success (368)
- Tiếng anh Lớp 11 iLearn Smart World (104)
- Tiếng Anh Lớp 12 cũ (168)
- Tiếng Anh Lớp 6 Friends Plus (114)
- Tiếng Anh Lớp 6 Global Success (174)
- Tiếng Anh Lớp 7 Friends Plus (160)
- Tiếng Anh Lớp 8 Friends plus (71)
- Tiếng anh Lớp 8 Global Success (79)
- Tiếng anh Lớp 8 iLearn Smart World (40)
- Tiếng Anh Lớp 9 Mới (211)
- Tin Học Lớp 10- CD (24)
- Tin Học Lớp 10- KNTT (33)
- Tin học Lớp 11 – KNTT (21)
- Tin Học Lớp 6 – CTST (41)
- Tin Học Lớp 6- KNTT (17)
- Tin Học Lớp 7- CTST (14)
- Tin Học Lớp 7- KNTT (16)
- Tin học Lớp 8 – CD (36)
- Tin học Lớp 8 – CTST (10)
- Tin học Lớp 8 – KNTT (5)
- Tin Học Lớp 9 (21)
- Toán 10 sách Chân trời sáng tạo (42)
- Toán Lớp 1 – KNTT (1)
- Toán Lớp 10- CD (44)
- Toán Lớp 10- CTST (39)
- Toán Lớp 10- KNTT (161)
- Toán Lớp 11 – CD (19)
- Toán Lớp 11 – CTST (44)
- Toán Lớp 11 – KNTT (46)
- Toán Lớp 12 (123)
- Toán Lớp 6 – CTST (62)
- Toán Lớp 6 – KNTT (102)
- Toán Lớp 7- CTST (52)
- Toán Lớp 7- KNTT (74)
- Toán Lớp 8 – CD (23)
- Toán Lớp 8 – CTST (21)
- Toán Lớp 8 – KNTT (34)
- Toán Lớp 9 (194)
- Tóm tắt Ngữ văn (16)
- Trắc nghiệm Ngữ Văn (75)
- Trắc nghiệm Toán 9 (61)
- Trải nghiệm hướng nghiệp Lớp 11 – KNTT (8)
- Văn mẫu 12 phân tích chuyên sâu (12)
- Văn mẫu 9 (273)
- Vật Lí Lớp 10- CD (39)
- Vật Lí Lớp 10- KNTT (61)
- Vật Lí Lớp 11 – CD (18)
- Vật lí Lớp 11 – CTST (20)
- Vật lí Lớp 11 – KNTT (26)
- Vật Lý Lớp 9 (217)