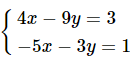tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 2: Hệ hai phương trình bậc nhất hai ẩn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 2: Hệ hai phương trình bậc nhất hai ẩn
a) (−4;5),
{7x−5y=−53−2x+9y=53
b) (3;−11),
{0,2x+1,7y=−18,13,2x−y=20,6
c) (1,5;2),(3;7),
{10x−3y=9−5x+1,5y=−4,5
d) (1;8),
{5x+2y=9x−14y=5
Phương pháp giải:
Sử dụng:
Ta thay giá trị x và y vào từng phương trình của hệ. Nếu cặp số (x;y) thỏa mãn cả hai phương trình của hệ thì cặp số đó là một nghiệm của hệ phương trình đã cho.
Lời giải:
a)
Thay x=−4;y=5 vào từng phương trình của hệ:
+) 7.(−4)–5.5=−53⇔−53=−53 (luôn đúng)
+) −2.(−4)+9.5=53⇔53=53 (luôn đúng)
Vậy cặp (−4;5) là nghiệm của hệ phương trình
{7x−5y=−53−2x+9y=53
b)
Thay x=3;y=−11 vào từng phương trình của hệ:
+)0,2.3+1,7.(−11)=−18,1⇔−18,1=−18,1(luôn đúng)
+) 3,2.3−(−11)=20,6⇔20,6=20,6 (luôn đúng)
Vậy cặp (3;−11) là nghiệm của hệ phương trình
{0,2x+1,7y=−18,13,2x−y=20,6
c)
Thay x=1,5;y=2 vào từng phương trình của hệ:
+) 10.1,5–3.2=9⇔9=9 (luôn đúng)
+)−5.1,5+1,5.2=−4,5⇔−4,5=−4,5(luôn đúng)
Vậy cặp (1,5;2) là nghiệm của hệ phương trình
{10x−3y=9−5x+1,5y=−4,5
Thay x=3;y=7 vào từng phương trình của hệ:
10.3–3.7=9⇔9=9 (luôn đúng)
−5.3+1,5.7=−4,5⇔−4,5=−4,5(luôn đúng)
Vậy cặp (3;7) là nghiệm của hệ phương trình
{10x−3y=9−5x+1,5y=−4,5
d)
Thay x=1;y=8 vào phương trình thứ nhất của hệ:
5.1+2.8=9⇔21=9 (vô lí)
Vậy cặp (1;8) không phải là nghiệm của hệ phương trình
{5x+2y=9x−14y=5
a)
b) {2,3x+0,8y=52y=6
c) {3x=−5x+5y=−4
d) {3x−y=16x−2y=5
Phương pháp giải:
Sử dụng:
– Ta biến đổi các hệ phương trình đã cho về dạng {y=ax+by=a′x+b′(nếu có thể)
– Với hai đường thẳng (d):y=ax+b và (d′):y=a′x+b′ trong đó a và a′ khác 0. Ta so sánh các hệ số a, a′; b, b′.
+) Nếu a≠a′ thì d cắt d′⇒ hệ đã cho có một nghiệm duy nhất.
+) Nếu a=a′, b≠b′ thì d song song với d′⇒ hệ đã cho vô nghiệm.
+) Nếu a=a′, b=b′ thì d trùng với d′⇒ hệ đã cho có vô số nghiệm.
Lời giải:
a)
{4x−9y=3−5x−3y=1⇔{y=49x−13(d)y=−53x−13(d′)
Ta có a=49, a′=−53 nên a≠a′.
Do đó (d),(d′) cắt nhau.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
b)
{2,3x+0,8y=52y=6⇔{y=−238x+254y=3
Đường thẳng y=−238x+254 cắt hai trục tọa độ, đường thẳng y=3 song song với trục hoành nên hai đường thẳng trên cắt nhau.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
c)
{3x=−5x+5y=−4⇔{x=−53y=−15x−45
Đường thẳng x=−53 song song với trục tung, đường thẳng y=−15x−45 cắt hai trục tọa độ nên hai đường thẳng đó cắt nhau.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
d)
{3x−y=16x−2y=5⇔{y=3x−1(d)y=3x−52(d′)
Ta có a=3,b=−1 và a′=3,b′=−52 nên a=a′,b≠b′.
Do đó (d),(d′) song song với nhau.
Vậy hệ phương trình đã cho vô nghiệm.
a) Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ có nghiệm duy nhất
b) Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ vô nghiệm
c) Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ có vô số nghiệm
Phương pháp giải:
Sử dụng:
– Với hai đường thẳng (d):y=ax+b và (d′):y=a′x+b′ trong đó a và a′ khác 0. Ta so sánh các hệ số a, a′; b, b′.
+) Nếu a≠a′ thì d cắt d′⇒ hệ đã cho có một nghiệm duy nhất.
+) Nếu a=a′, b≠b′ thì d song song với d′⇒ hệ đã cho vô nghiệm.
+) Nếu a=a′, b=b′ thì d trùng với d′⇒ hệ đã cho có vô số nghiệm.
Lời giải:
a)
Ta có 3x−2y=5⇔y=32x−52
Ta cần thêm một phương trình bậc nhất hai ẩn để được một hệ có nghiệm duy nhất. Do đó ta phải thêm đường thẳng có hệ số góc khác 32.
Chẳng hạn ta thêm đường thẳng
y=23x+13⇔2x−3y=−1
Khi đó ta có hệ phương trình
{3x−2y=52x−3y=−1
và hệ này có nghiệm duy nhất.
b)
Ta cần thêm một phương trình bậc nhất hai ẩn để được môt hệ vô nghiệm. Do đó ta phải thêm đường thẳng có hệ số góc bằng 32 và tung độ gốc khác −52.
Chẳng hạn ta thêm đường thẳng
y=32x−12⇔3x−2y=1
Khi đó ta có hệ phương trình
{3x−2y=53x−2y=1
và hệ này vô nghiệm.
c)
Ta cần thêm một phương trình bậc nhất hai ẩn để được một hệ có vô số nghiệm. Do đó ta phải thêm đường thẳng có hệ số góc bằng 32 và tung độ gốc bằng −52.
Chẳng hạn ta thêm đường thẳng
y=32x−52 ⇔ 6x−4y=10
Khi đó ta có hệ phương trình
{3x−2y=56x−4y=10
và hệ này có vô số nghiệm.
{ax+by=ca′x+b′y=c′
a) Có nghiệm duy nhất
b) Vô nghiệm
c) Có vô số nghiệm
Áp dụng:
a) Hãy lập một hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất
b) Hãy lập một hệ hai phương trình bậc nhất hai ẩn vô nghiệm
c) Hãy lập một hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm
Phương pháp giải:
Sử dụng:
– Với hai đường thẳng (d):y=ax+b và (d′):y=a′x+b′ trong đó a và a′ khác 0. Ta so sánh các hệ số a, a′; b, b′.
+) Nếu a≠a′ thì d cắt d′⇒ hệ đã cho có một nghiệm duy nhất.
+) Nếu a=a′, b≠b′ thì d song song với d′⇒ hệ đã cho vô nghiệm.
+) Nếu a=a′, b=b′ thì d trùng với d′⇒ hệ đã cho có vô số nghiệm.
Lời giải:
Ta chia ra các trường hợp:
1. Trường hợp a,b,a′,b′ đều khác 0
{ax+by=ca′x+b′y=c′
⇔{y=−abx+cb(d)y=−a′b′x+c′b′(d′)
a) Hệ phương trình đã cho có nghiệm duy nhất khi hai đường thẳng (d) và (d′) cắt nhau tức là hai đường thẳng này có hệ số góc khác nhau. Do đó ab≠a′b′ hay aa′≠bb′
b) Hệ phương trình đã cho vô nghiệm khi hai đường thẳng (d) và (d′) song song. Tức là hai đường thẳng này có hệ số góc bằng nhau và tung độ gốc khác nhau. Do đó:
{ab=a′b′cb≠c′b′ hay aa′=bb′≠cc′ (nếu c′≠0) hoặc a′a=b′b≠c′c (nếu c≠0)
c) Hệ phương trình đã cho có vô số nghiệm khi hai đường thẳng (d) và (d′) trùng nhau tức là hai đường thẳng này có cùng hệ số góc và tung độ gốc. Do đó
{ab=a′b′cb=c′b′ hay aa′=bb′=cc′ (nếu c′≠0) hoặc a′a=b′b=c′c (nếu c≠0)
2. Trường hợp a=0 và a′≠0
{ax+by=ca′x+b′y=c′
⇔{y=cby=−a′b′x+c′b′(nếu b′≠0)
Hoặc
{ax+by=ca′x+b′y=c′
⇔{y=cbx=c′a′(nếu b′=0)
Vì đường thẳng y=cb song song hoặc trùng với trục Ox, còn đường thẳng y=−a′b′x+c′b′ và đường thẳng x=c′a′ luôn luôn cắt trục hoành nên đường thẳng y=cb luôn luôn cắt hai đường thẳng y=−a′b′x+c′b′ và x=c′a′ . Do đó hệ phương trình đã cho có nghiệm duy nhất.
Tương tự trường hợp a≠0 và a′=0 , hệ phương trình đã cho cũng có nghiệm duy nhất.
3. Trường hợp a=a′=0
{ax+by=ca′x+b′y=c′⇔{y=cby=c′b′
Hệ đã cho vô nghiệm khi cb≠c′b′
Hệ đã cho có vô số nghiệm khi cb=c′b′
4. Trường hợp b=0;b′≠0
{ax+by=ca′x+b′y=c′⇔{x=cay=−a′b′x+c′b′
Vì đường thẳng x=ca song song hoặc trùng với trục Oy, còn đường thẳng y=−a′b′x+c′b′ luôn cắt trục Oy nên hai đường thẳng này luôn luôn cắt nhau. Do đó hệ đã cho có nghiệm duy nhất.
Tương tự trường hợp b≠0 và b′=0 , hệ phương trình đã cho cũng có nghiệm duy nhất.
5. Trường hợp b=b′=0
{ax+by=ca′x+b′y=c′⇔{x=cax=c′a′
Hệ vô nghiệm khi hai đường thẳng đó song song: ca≠c′a′
Hệ có vô số nghiệm khi hai đường thẳng đó trùng nhau: ca=c′a′
Áp dụng
a) Hệ phương trình {2x+3y=13x−y=3 có một nghiệm duy nhất vì aa′≠bb′(23≠3−1)
b) Hệ phương trình
{2x+3y=14x+6y=5 vô nghiệm vì aa′=bb′≠cc′(24=36≠15)
c) Hệ phương trình {2x+3y=14x+6y=2 có vô số nghiệm vì aa′=bb′=cc′(24=36=12)
a) {2x+3y=7x−y=6
b) {3x+2y=132x−y=−3
c) {x+y=13x+0y=12
d) {x+2y=60x−5y=10
Phương pháp giải:
Sử dụng:
– Ta biến đổi hệ phương trình đã cho về dạng {y=ax+by=a′x+b′
+) Vẽ hai đường thẳng y=ax+b và y=a′x+b′ trong cùng một hệ trục tọa độ.
+) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ.
+) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ.
Lời giải:
a)
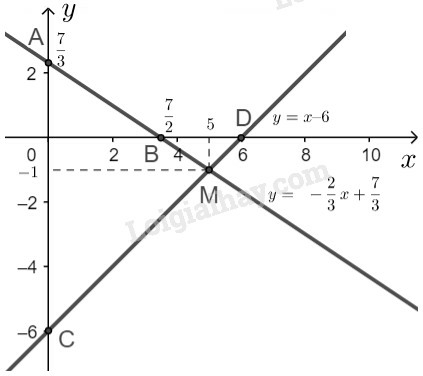
{2x+3y=7x−y=6⇔{y=−23x+73y=x−6
– Vẽ đường thẳng y=−23x+73:
Cho x=0⇒y=73 ta được A(0;73)
Cho y=0⇒x=72 ta được B(72;0)
Đường thẳng y=−23x+73 là đường thẳng đi qua hai điểm A, B.
– Vẽ đường thẳng y=x–6:
Cho x=0⇒y=−6 ta được C(0;−6)
Cho y=0⇒x=6 ta được D(6;0)
Đường thẳng y=x–6 là đường thẳng đi qua hai điểm C, D.
– Quan sát hình vẽ, ta thấy hai đường thẳng y=−23x+73 và y=x–6 cắt nhau tại điểm M(5;−1).
Thay x=5,y=−1 vào hệ phương trình đã cho ta được:
{2.5+3.(−1)=75−(−1)=6⇔{7=76=6(luôn đúng)
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x;y)=(5;−1).
b)
{3x+2y=132x−y=−3
⇔{y=−32x+132y=2x+3
– Vẽ đường thẳng y=−32x+132:
Cho x=0⇒y=132 ta được E(0;132)
Cho y=0⇒x=133 ta được F((133;0)
Đường thẳng y=−32x+132 là đường thẳng đi qua hai điểm E, F
– Vẽ đường thẳng y=2x+3:
Cho x=0⇒y=3 ta được G(0;3)
Cho y=0⇒x=−32 ta được H(−32;0)
Đường thẳng y=2x+3 là đường thẳng đi qua hai điểm G, H.
– Quan sát hình vẽ, ta thấy hai đường thẳng y=−32x+132 và y=2x+3 cắt nhau tại điểm N(1;5).
Thay x=1,y=5 vào hệ phương trình đã cho ta được:
{3.1+2.5=132.1−5=−3⇔{13=13−3=−3(luôn đúng)
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x;y)=(1;5).
c)
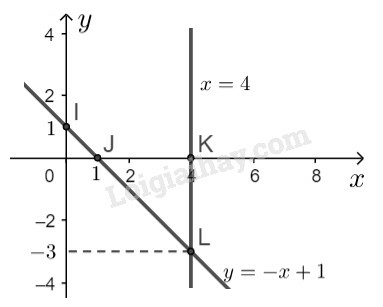
{x+y=13x+0y=12⇔{y=−x+1x=4
– Vẽ đường thẳng y=−x+1:
Cho x=0⇒y=1 ta được I(0;1)
Cho y=0⇒x=1 ta được J(1;0)
Đường thẳng y=−x+1 là đường thẳng đi qua hai điểm I, J.
– Vẽ đường thẳng x=4:
Đường thẳng x=4 đi qua điểm K(4;0) và song song với trục tung.
– Quan sát hình vẽ, ta thấy hai đường thẳng y=−x+1 và x=4 cắt nhau tại điểm L(4;−3).
Thay x=4,y=−3 vào hệ phương trình đã cho ta được:
{4+(−3)=13.4+0.(−3)=12⇔{1=112=12(luôn đúng)
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x;y)=(4;−3).
d)
{x+2y=60x−5y=10
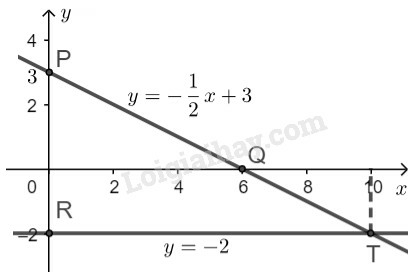
⇔{y=−12x+3y=−2
– Vẽ đường thẳng y=−12x+3:
Cho x=0⇒y=3 ta được P(0;3)
Cho y=0⇒x=6 ta được Q(6;0)
Đường thẳng y=−12x+3 là đường thẳng đi qua hai điểm P, Q.
– Vẽ đường thẳng y=−2:
Đường thẳng y=−2 đi qua điểm R(0;−2) và song song với trục hoành.
– Quan sát hình vẽ, ta thấy hai đường thẳng y=−12x+3 và y=−2 cắt nhau tại điểm T(10;−2).
Thay x=10,y=−2 vào hệ phương trình đã cho ta được:
{10+2.(−2)=60.10−5.(−2)=10⇔{6=610=10(luôn đúng)
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x;y)=(10;−2).
{x+0y=−25x−y=−9
a) Minh họa hình học tập nghiệm của hệ phương trình đã cho. Từ đó xác định nghiệm của hệ.
b) Nghiệm của hệ này có phải là nghiệm của phương trình 3x–7y=1 hay không?
Phương pháp giải:
Sử dụng:
– Ta biến đổi hệ phương trình đã cho về dạng {x=ay=a′x+b′
+) Vẽ hai đường thẳng x=a và y=a′x+b′ trong cùng một hệ trục tọa độ.
+) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ.
+) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ.
– Một cặp số (x0;y0) là một nghiệm của phương trình ax+by=c (a≠0 hoặc b≠0) khi và chỉ khi ax0+by0=c.
Lời giải:
a)
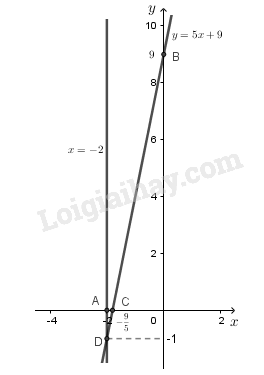
{x+0y=−25x−y=−9⇔{x=−2y=5x+9
– Vẽ đường thẳng x=−2:
Đường thẳng x=−2 là đường thẳng đi qua điểm A(−2;0) và song song với trục tung.
– Vẽ đường thẳng y=5x+9:
Cho x=0⇒y=9 ta được B(0;9)
Cho y=0⇒x=−95 ta được C(−95;0)
Đường thẳng y=5x+9 là đường thẳng đi qua hai điểm B, C
– Quan sát hình vẽ, ta thấy hai đường thẳng x=−2 và y=5x+9 cắt nhau tại điểm D(−2;−1).
Thay x=−2,y=−1 vào hệ phương trình đã cho ta được:
{−2+0.(−1)=−25.(−2)−(−1)=−9⇔{−2=−2−9=−9(luôn đúng)
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x;y)=(−2;−1).
b)
Thay x=−2;y=−1 vào phương trình 3x–7y=1 ta có:
3.(−2)−7.(−1)=1⇔1=1 (luôn đúng)
Vậy cặp (x;y)=(−2;−1) là nghiệm của phương trình 3x–7y=1.
Hỏi đường thẳng (d3):3x+2y=10 có đi qua giao điểm của (d1) và (d2) hay không?
Phương pháp giải:
Sử dụng:
– Vẽ đường thẳng có phương trình ax+by=c, (a,b≠0):
Ta có ax+by=c⇔y=−abx+cb.
+) Cho x=0⇒y=cb ta được A(0;cb)
+) Cho y=0⇒x=ca ta được B(ca;0)
Đường thẳng đã cho là đường thẳng đi qua hai điểm A, B.
– Hoành độ giao điểm của hai đường thẳng y=ax+b và y=a′x+b′ là nghiệm của phương trình: ax+b=a′x+b′.
Giải phương trình trên ta tìm được x. Thay giá trị của x vào phương trình y=ax+b hoặc y=a′x+b′, ta tìm được tung độ giao điểm.
– Đường thẳng ax+by=c đi qua điểm M(x0;y0) ⇔ax0+by0=c.
Lời giải:
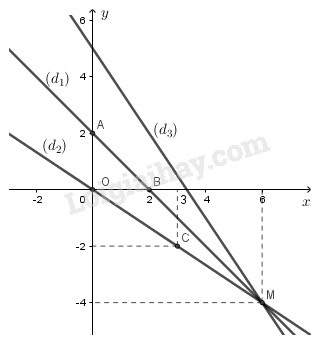
– Vẽ đường thẳng (d1):x+y=2
Ta có (d1):x+y=2⇔y=−x+2
Cho x=0⇒y=2 ta được A(0;2)
Cho y=0⇒x=2 ta được B(2;0)
Đường thẳng (d1) là đường thẳng đi qua hai điểm A, B.
– Vẽ đường thẳng (d2):2x+3y=0
Ta có (d2):2x+3y=0⇔y=−23x
Cho x=0⇒y=0 ta được O(0;0)
Cho x=3⇒y=−2 ta được C(3;−2)
Đường thẳng (d2) là đường thẳng đi qua hai điểm O, C.
– Hoành độ giao điểm M của hai đường thẳng (d1) và (d2) là nghiệm của phương trình:
−x+2=−23x⇔13x=2⇔x=6
Suy ra tung độ giao điểm M là y=−6+2=−4
Vậy tọa độ giao điểm của hai đường thẳng (d1) và (d2) là M(6;−4).
Thay x=6;y=−4 vào phương trình đường thẳng (d3) ta được:
3.6+2.(−4)=10⇔18−8=10⇔10=10 (luôn đúng).
Vậy đường thẳng (d3):3x+2y=10 đi qua giao điểm của (d1) và (d2).
(d1):3x+2y=13(d2):2x+3y=7(d3):x−y=6(d4):5x−0y=25?
Phương pháp giải:
Sử dụng:
– Tìm giao điểm M của hai đường thẳng bất kì:
Hoành độ giao điểm M của hai đường thẳng y=ax+b và y=a′x+b′ là nghiệm của phương trình: ax+b=a′x+b′.
Giải phương trình trên ta tìm được x. Thay giá trị của x vào phương trình y=ax+b hoặc y=a′x+b′, ta tìm được tung độ giao điểm.
– Nếu hai đường thẳng còn lại cùng đi qua điểm M thì 4 đường thẳng đã cho đồng quy tại điểm M.
– Đường thẳng ax+by=c đi qua điểm M(x0;y0) ⇔ax0+by0=c.
Lời giải:
– Ta có (d2):2x+3y=7⇔y=−23x+73
(d3):x−y=6⇔y=x–6
Hoành độ giao điểm M của hai đường thẳng (d2) và (d3) là nghiệm của phương trình:
−23x+73=x−6⇔53x=253⇔x=5
Suy ra tung độ giao điểm M là y=5−6=−1
Vậy tọa độ giao điểm của hai đường thẳng (d2) và (d3) là M(5;−1).
– Nếu (d1),(d4) cùng đi qua điểm M(5;−1) thì bốn đường thẳng đã cho đồng quy.
Thay x=5;y=−1 vào phương trình đường thẳng (d1) ta được:
3.5+2.(−1)=13⇔13=13 (luôn đúng)
Do đó (d1) đi qua M(5;−1).
Thay x=5;y=−1 vào phương trình đường thẳng (d4) ta được:
5.5−0.(−1)=25⇔25=25 (luôn đúng)
Do đó (d4) đi qua M(5;−1).)
Vậy bốn đường thẳng đã cho đồng quy tại M(5;−1).
Bài tập bổ sung (trang 8 SBT Toán 9)
a){3x=6x−3y=2
b){3x+5y=152y=−7
c){3x=62y=−7
Phương pháp giải:
Sử dụng:
– Cho hệ hai phương trình bậc nhất hai ẩn:
(I) {ax+by=c (d)a′x+b′y=c′ (d′)
+ Nếu (d) cắt (d′) thì hệ (I) có một nghiệm duy nhất.
+ Nếu (d) song song với (d′) thì hệ (I) vô nghiệm.
+ Nếu (d) trùng với (d′) thì hệ (I) có vô số nghiệm.
Lời giải:
a){3x=6x−3y=2⇔{x=2y=13x−23
Đường thẳng x=2 song song với trục tung, đường thẳng y=13x−23 cắt trục tung nên hai đường thẳng trên cắt nhau. Vậy hệ phương trình đã cho có nghiệm duy nhất.
b){3x+5y=152y=−7 ⇔{y=−35x+3y=−72
Đường thẳng y=−72 song song với trục hoành, đường thẳng y=−35x+3 cắt trục hoành nên hai đường thẳng trên cắt nhau. Vậy hệ phương trình đã cho có nghiệm duy nhất.
c){3x=62y=−7 ⇔{x=2y=−72
Đường thẳng x=2 song song với trục tung, đường thẳng y=−72 cắt trục tung nên hai đường thẳng trên cắt nhau. Vậy hệ phương trình đã cho có nghiệm duy nhất.
a){2x+0y=54x+0y=7
b){2x+0y=54x+0y=10
c){0x+3y=−80x−21y=56
d){0x+3y=−80x−21y=50
Phương pháp giải:
Sử dụng:
– Cho hệ hai phương trình bậc nhất hai ẩn:
(I) {ax+by=c (d)a′x+b′y=c′ (d′)
+ Nếu (d) cắt (d′) thì hệ (I) có một nghiệm duy nhất.
+ Nếu (d) song song với (d′) thì hệ (I) vô nghiệm.
+ Nếu (d) trùng với (d′) thì hệ (I) có vô số nghiệm.
Lời giải:
a){2x+0y=54x+0y=7⇔{x=52x=74
Đường thẳng x=52 song song với trục tung, đường thẳng x=74 cũng song song với trục tung nên chúng song song với nhau (vì 52≠74)
Vậy hệ phương trình đã cho vô nghiệm.
b) Ta có 2x+0y=5⇔x=52;
4x+0y=10⇔x=52
Do đó đường thẳng 2x+0y=5 và đường thẳng 4x+0y=10 trùng nhau.
Vậy hệ phương trình đã cho có vô số nghiệm.
c) Ta có 0x+3y=−8⇔y=−83;
0x−21y=56⇔y=−83
Do đó đường thẳng 0x+3y=−8 và đường thẳng 0x−21y=56 trùng nhau. Vậy hệ phương trình đã cho có vô số nghiệm.
d){0x+3y=−80x−21y=50⇔{y=−83y=−5021
Đường thẳng y=−83 và đường thẳng y=−5021 đều song song với trục hoành nên chúng song song với nhau. Vậy hệ phương trình đã cho vô nghiệm.
