SBT Toán 9 Bài 1: Góc ở tâm. Số đo cung | Giải SBT Toán lớp 9 

a) Từ 1 giờ đến 3 giờ kim giờ quay được 1 góc ở tâm bằng bao nhiêu độ?

b) Cũng hỏi như thế từ 3 giờ đến 6 giờ?

Phương pháp giải:

Ta sử dụng kiến thức: Góc ở có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

Lời giải:

Vì trên đồng hồ có 12 chữ số nên mặt đồng hồ được chia ra thành 12 cung tròn bằng nhau, mỗi cung tròn tương ứng với góc ở tâm bằng 3600:12=30o.

a) Từ 1 giờ đến 3 giờ thì kim giờ quay được một góc ở tâm bằng 2.300=60o.

b) Từ 3 giờ đến 6 giờ thì kim giờ quay được một góc ở tâm bằng 3.300=90o.

Lời giải:

Một vòng quay của kim phút là 60 phút tương ứng với 360°. Như vậy mỗi phút tương ứng với 3600:60=60. Đồng hồ chạy chậm 25 phút thì phải quay kim phút một góc ở tâm là 60.25=1500.

Muốn cắt chỉ bằng một nhát kéo thì phải gấp tờ giấy đó thành một hình có góc ở tâm bằng bao nhiều độ?

Phương pháp giải:

Ta sử dụng kiến thức: Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. 

Lời giải:

Đầu tiên ta gấp đôi tờ giấy, ta chọn điểm làm tâm rồi chia tờ giấy ra thành 5 phần với 5 góc ở tâm bằng nhau, mỗi góc bằng 180o:5=36o.

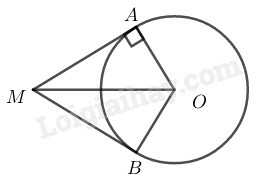
Tính số đo góc ở tâm AOB^?

Phương pháp giải:

Lời giải:

Xét đường trong (O) có: MA⊥OA (tính chất tiếp tuyến)

Trong ∆MAO có OAM^=900, ta có:

cos⁡AOM^=OAOM=R2R=12

⇒AOM^=600

Lại có OM là tia phân giác của góc AOB (tính chất 2 tiếp tuyến MA, MB cắt nhau nhau tại M)

Suy ra AOM^=12AOB^ 

⇒AOB^=2AOM^=1200

Phương pháp giải:

Ta sử dụng kiến thức:

+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

+) Trong tam giác đều mỗi góc bằng 60o.

+) Số đo của nửa đường tròn bằng 180o.

Lời giải:

Điểm D có 2 trường hợp :

∗) Nếu điểm D nằm giữa C và B

Ta có C điểm chính giữa của cung AB nên:

sđBC⏜=sđAC⏜=90o

Ta lại có CD=R (gt)

Suy ra : OC=OD=CD=R

⇒ΔOCD đều ⇒COD^=60o

⇒sđCD⏜=COD^=60o

⇒sđBD⏜=sđBC⏜−sđCD⏜=90o−60o=30o

Suy ra BOD^=sđBD⏜=30o

∗) Nếu D nằm giữa C và A ta có : CD=OC=OD=R

⇒ΔOCD đều ⇒COD^=60o

sđCD⏜=COD^=60o

sđBD⏜=sđBC⏜+sđCD⏜=90o+60o=150o

Suy ra BOD^=sđBD⏜=150o

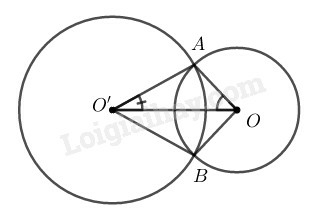
a) Số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O′;R′).

b) Số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O;R′).

c) Số đo hai cung nhỏ bằng nhau.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Số đo của cung lớn bằng hiệu giữa 360o và số đo cung nhỏ(có chung hia mút với cung lớn).

+) Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

+) Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.

+) Hai cung được là bằng nhau nếu chúng có số đo bằng nhau.

+) Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.

Lời giải:

a) Trong (O;R) ta có: AOB^=sđAB⏜ (nhỏ)

Trong (O′;R) ta có: AO′B^=sđAB⏜ (nhỏ)

Vì số đo cung AB nhỏ của (O;R) lớn hơn số đo cung AB nhỏ của (O′;R′)

Suy ra: AOB^>AO′B^                   (1)

Xét hai tam giác ΔAOO′ và ΔBOO′ có:

+) O′A=O′B=R′

+) OA=OB=R

+) OO′ cạnh chung

Nên ΔAOO′=ΔBOO′ (c.c.c)

⇒AOO′^=BOO′^=12AOB^          (2)

AO′O^=BO′O^=12AO′B^          (3)

Từ (1), (2) và (3) suy ra: AOO′^>AO′O^

Trong ΔAOO′ ta có:  AOO′^>AO′O^

Suy ra: O′A>OA (bất đẳng thức tam giác) hay R′>R 

Chú ý: Nếu các em vẽ hình như dưới đây thì ta lấy đối xứng đường tròn (O) qua trục AB để chứng minh như trên.

b) Trong (O;R) số đo cung lớn AB cộng với số đo cung nhỏ AB bằng 360o

Mà số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O′;R′)

Suy ra số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ của (O′;R′)

Chứng minh tương tự câu a) ta có: R>R′.

c) Số đo hai cung nhỏ của (O;R) và (O′;R′) bằng nhau

⇒AOB^=AO′B^

Suy ra: AOO′^=AO′O^⇒ΔAOO′ cân tại A nên OA=OA′ hay R=R′.

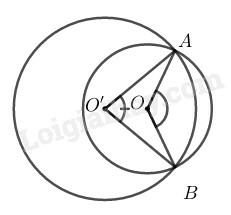
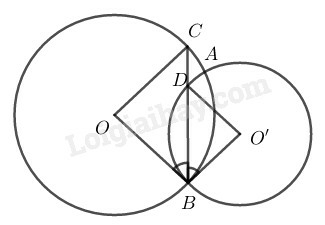
Hãy so sánh các góc ở tâm BOC và BO′D.

Hướng dẫn. Sử dụng các tam giác cân OBC, O′BD.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Trong tam giác cân, hai góc ở đáy bằng nhau.

+) Góc có đỉnh trùng với tâm đường tròn gọi là góc ở tâm.

Lời giải:

Trong (O) ta có:

ΔOBC cân tại O (vì OB=OC= bán kính)

⇒BOC^=1800−2.OBC^(1)

Trong (O′) ta có:

ΔBO′D cân tại O′ (vì O′D=O′D= bán kính)

⇒BO′D^=1800−2.O′BD^(2)

Lại có OBC^=O′BD^ (3) (vì BC là phân giác của OBO′^)

Từ (1), (2) và (3) suy ra: BOC^=BO′D^.

Ta sử dụng kiến thức:

+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

+) Số đo của cung lớn bằng hiệu giữa  360o và số đo cung nhỏ (có chung hai đầu mút với cung lớn).

Lời giải:

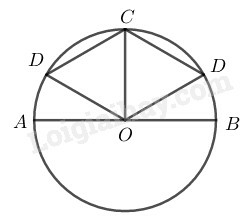
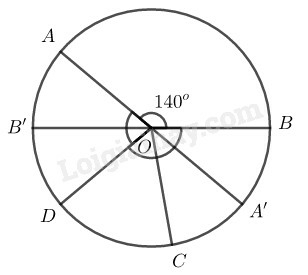
Vì  cung AD nhận B làm điểm chính giữa, cung CB nhận A là điểm chính giữa nên AB⏜=BD⏜=AC⏜

⇒AOB^=BOD^=AOC^=1400 

Kẻ đường kính AA′,BB′ ta có:

AOB^+AOB′^=1800 (hai góc kề bù)

⇒AOB′^=1800−AOB^=1800−1400=400

Suy ra: BOA′^=AOB′^=400 (hai góc đối đỉnh)

B′OD^+BOD^=1800 (hai góc kề bù)

⇒B′OD^=1800−BOD^=1800−1400=400

AOC^=AOB′^+B′OD^+DOC^

⇒DOC^=AOC^−AOB′^−B′OD^=1400−400−400=600

sđCD⏜(nhỏ)=COD^=600

sđCD⏜(lớn)=360o−sđCD⏜(nhỏ)=360o−60o=300o

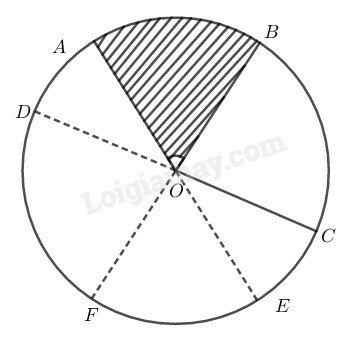
Hướng dẫn: Xét 3 trường hợp:

a) Tia OC nằm trong góc đối đỉnh của góc ở tâm AOB^.

b) Tia OC trùng với tia đối của một cạnh của góc ở tâm AOB^.

c) Tia OC nằm trong một góc kề bù với góc ở tâm AOB^.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Nếu C là một điểm trên cung AB thì: sđAB⏜=sđAC⏜+sđCB⏜.

+) Số đo của nửa đường tròn bằng 180o.

+) Số đo của cung lớn bằng hiệu giữa  360o và số đo cung nhỏ (có chung hai đầu mút với cung lớn).

+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Lời giải:

a) Trường hợp tia OC nằm trong góc đối đỉnh với AOB^ 

Kẻ đường kính CD

Suy ra: OD nằm giữa OA và OB nên điểm D nằm trên cung nhỏ cung AB⏜

⇒sđAD⏜(nhỏ)+sđBD⏜(nhỏ)=sđAB⏜(nhỏ) (1)

Vì OA nằm giữa OC và OD nên điểm A nằm trên cung nửa đường tròn CD.

⇒sđAD⏜(nhỏ)+sđAC⏜(nhỏ)=180o (2)

Vì OB nằm giữa OC và OD nên điểm B nằm trên cung nửa đường tròn CD.

⇒sđBD⏜(nhỏ)+sđBC⏜(nhỏ)=180o (3)

Cộng từng vế (2) và (3):

sđAD⏜(nhỏ)+sđAC⏜(nhỏ)+sđBD⏜(nhỏ)+sđBC⏜(nhỏ)=360o (4)

Từ (1) và (4) suy ra: sđAC⏜(nhỏ)+sđBC⏜(nhỏ)+sđAB⏜(nhỏ)=360o

⇒sđAC⏜(nhỏ)+sđBC⏜(nhỏ)=360o−sđAB⏜(nhỏ)

Mà 360o−sđAB⏜(nhỏ)=sđAD⏜(lớn)

Vậy với cung lớn AB⏜ ta có: sđAB⏜=sđAC⏜+sđBC⏜

b) Trường hợp tia OC trùng với tia đối của một cạnh của góc ở tâm AOB^

Do tia OC trùng với tia đối của một cạnh của góc ở tâm AOB^, ta có:

AOB^+BOC^=180o; AOC^=180o

⇒AOB^+BOC^+AOC^=360o

⇒AOC^+BOC^=360o−AOB^

Suy ra: sđAB⏜+sđBC⏜(nhỏ)=360o−sđAB⏜(nhỏ)

Vậy với cung lớn AB⏜ ta có: sđAB⏜=sđAC⏜(nhỏ)+sđBC⏜

c) Trong hợp tia OC nằm trong góc kề bù với góc ở tâm AOB^

Kẻ đường kính AE.

Theo trường hợp b) ta có:

sđAB⏜(lớn)=sđAE⏜(nhỏ)+sđBE⏜(nhỏ)

Ta xét trường hợp C nằm trên cung nhỏ EB⏜:

sđEB⏜(nhỏ)=sđEC⏜(nhỏ)+sđCB⏜(nhỏ)

⇒ sđAB⏜(lớn)=sđAE⏜+sđEC⏜(nhỏ)+sđCB⏜(nhỏ)

Theo kết quả trường hợp b) ta có:

sđAE⏜+sđEC⏜(nhỏ)=sđAC⏜(lớn)

Vậy với cung AB⏜ lớn ta có: sđAB⏜=sđAC⏜+sđCB⏜

Trong trường hợp OC nằm trên góc đối với góc ở tâm BOE^ chứng minh tương tự.

Trong trường hợp OC nằm trên góc đối đỉnh với góc ở tâm AOB^ chứng minh ở trường hợp a).

Bài tập bổ sung (trang 100 SBT Toán 9)

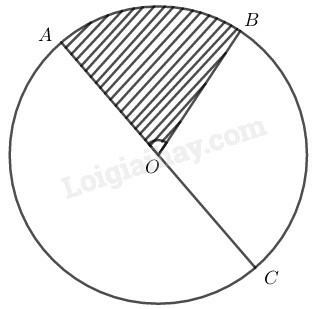
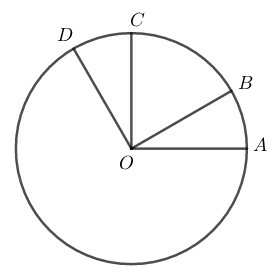
a) Đọc tên các góc ở tâm có số đo nhỏ hơn 180o.

b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.

c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 180o).

d) So sánh hai cung nhỏ AB và BC. 

Phương pháp giải:

Ta sử dụng kiến thức:

+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

+) Cung nhỏ có số đo nhỏ hơn 180o.

+) Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

Lời giải:

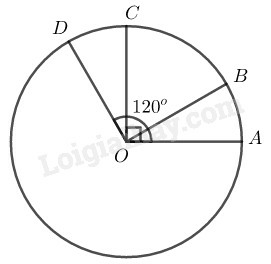
a) Các góc ở tâm có số đo nhỏ hơn 180o là:

AOB^,AOC^,AOD^,BOC^,BOD^,COD^

b) OA⊥OC⇒AOC^=900

OB⊥OD⇒BOD^=900

AOB^+BOD^=AOD^

⇒AOB^=AOD^−BOD^=1200−900=300

AOC^+COD^=AOD^

⇒COD^=AOD^−AOC^=1200−900=300

AOB^+BOC^=AOC^

⇒BOC^=AOC^−AOB^=900−300=600

c) Các cung có số đo bằng nhau nhỏ hơn 180o là:

AB⏜=CD⏜; AC⏜=BD⏜

d) sđAB⏜=AOB^=300

sđBC⏜=BOC^=600

Suy ra: sđBC⏜ gấp đôi sđAB⏜

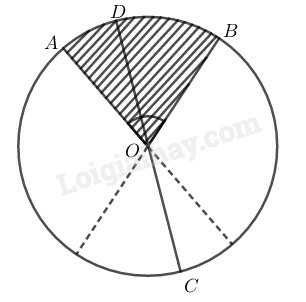
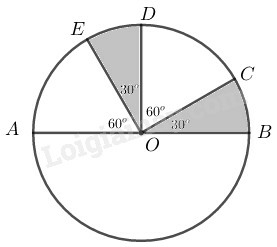
a) Đọc tên các góc ở tâm có số đo không lớn hơn 180o.

b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.

c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 180o).

d) So sánh hai cung nhỏ AE và BC.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

+) Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

+) Cung nhỏ có số đo nhỏ hơn 180o.

Lời giải:

a) Các góc ở tâm có số đo không quá 180o là:

AOB^,AOC^,AOD^,AOE^,BOC^,BOD^,BOE^,COD^,COE^,DOE^

b) Ta có: AOB^=1800

⇒sđAB⏜=180o

Ta có: sđBC⏜=16sđAB⏜

=16.1800=30o

⇒BOC^=sđBC⏜=30o

Ta có: sđ BD⏜=12sđAB⏜

=12.1800=900

⇒BOD^=sđBD⏜=900

Ta có: sđBE⏜=23sđBA⏜

=23.1800=1200

⇒BOE^=sđBE⏜=120o

BOC^+COE^=BOE^

⇒COE^=BOE^−BOC^

=1200−300=900

AOE^+BOE^=AOB^

⇒AOE^=AOB^−BOE^

=1800−1200=600

AOD^=BOD^=12AOB^=900

BOC^+COD^=BOD^

⇒COD^=BOD^−BOC^

=900−300=600

COD^+DOE^=COE^

⇒DOE^=COE^−COD^

=900−600=300

COA^+BOC^=1800

⇒AOC^=1800−BOC^

=1800−300=1500

c) Các cung có số đo nhỏ hơn 180o bằng nhau.

BC⏜=DE⏜; AE⏜=CD⏜; AD⏜=BD⏜; AD⏜=CE⏜; CE⏜=BD⏜.

d) sđAE⏜=AOE^=600

sđBC⏜=BOC^=300

Ta có số đo của cung AE⏜ gấp đôi số đo của cung BC⏜.