Giải SGK Toán 9 bài 5: Bảng Căn bậc hai hướng dẫn các bạn trả lời các câu hỏi trong SGK Toán lớp 9 trang 23. Lời giải Toán 9 giúp các em học sinh có thêm tài liệu tham khảo, so sánh đánh giá kết quả, từ đó học tốt môn Toán lớp 9. Dưới đây là chi tiết bài tập, các em tham khảo nhé.

Trả lời câu hỏi 1 Bài 5 trang 21 SGK Toán 9 Tập 1

Tìm:

a) sqrt {9,11} b) sqrt {39,82}

Lời giải chi tiết

a) sqrt {9,11} approx 3,018

b) sqrt {39,82} approx 6,310

Trả lời câu hỏi 2 Bài 5 trang 22 SGK Toán 9 Tập 1

Tìm: a) sqrt {911} b) sqrt {988}

Lời giải chi tiết:

a) sqrt {911} = sqrt {9,11}. sqrt {100} approx 3,018 .10 = 30,18

b) sqrt {988} = sqrt {9,88} . sqrt {100} approx 3,143 .10 = 31,43

Trả lời câu hỏi 3 Bài 5 trang 22 SGK Toán 9 Tập 1

Dùng bảng căn bậc hai, tìm giá trị gần đúng của nghiệm phương trình: x2=0,3982

Lời giải chi tiết:

begin{array}{l} {x^2} = 0,3982\ Leftrightarrow x = pm sqrt {0,3982} \ Leftrightarrow left[ begin{array}{l} x approx 0,631\ x approx - 0,631 end{array} right. end{array}

Bài 38 trang 23 SGK Toán 9 tập 1

Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

5,4;7,2;9,5;31;68.

Hướng dẫn giải:

Sử dụng máy tính cho kết quả như sau:

sqrt{5,4}approx2,324

sqrt{7,2}approx2,683

sqrt{9,5}approx3,082

sqrt{31}approx5,568

sqrt{68}approx8,246

So sánh kết quả, ta thấy:

sqrt{5,4}<sqrt{7,2}<sqrt{9,5}<sqrt{31}<sqrt{68}

Bài 39 trang 23 SGK Toán 9 tập 1

Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

115; 232; 571; 9691.

Hướng dẫn giải:

sqrt{232}approx15,232

sqrt{571}approx23,896

<sqrt{9691}approx98,443

So sánh kết quả, ta được:

10,724<15,232<23,896<98,443

Leftrightarrowsqrt{115}<sqrt{232}<sqrt{571}<sqrt{9691}

Bài 40 trang 23 SGK Toán 9 tập 1

Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

0,71;0,03;0,216;

0,811;0,0012; 0,000315.

Lời giải chi tiết

sqrt{0,71}approx 0,843

Giải bài tập SGK Toán lớp 9 bài 5: Bảng Căn bậc hai

sqrt{0,03}approx 0,173

sqrt{0,216}approx 0,465

sqrt{0,811}approx 0,901

sqrt{0,0012}approx 0,035

sqrt{0,000315}approx 0,018

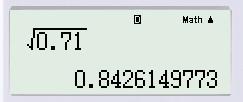
So sánh các số như sau:

Vì 0,018 <0,035 <0,173 <0,465<0,843< 0,901

Leftrightarrow sqrt{0,000315}<sqrt{0,0012}<sqrt{0,03}<sqrt{0,216}

<sqrt{0,71}< sqrt{0,811}.

Nhận thấy rằng, đối với các số từ 0 đến 1, lấy căn bậc hai ta luôn tìm được kết quả lớn hơn số ban đầu!

Bài 41 trang 23 SGK Toán 9 tập 1

Biết sqrt {9,119} approx 3,019. Hãy tính:

sqrt {911,9} ; sqrt {91190};

sqrt {0,09119} ; sqrt {0,0009119}

Lời giải chi tiết

Ta có:

+ sqrt {911,9} =sqrt {9,119.100}=sqrt{9,119}.sqrt{100}

=sqrt{9,119}.sqrt{10^2}=sqrt{9,119}.10

approx 3,019.10=30,19.

+ sqrt {91190} =sqrt {9,1190.10000}=sqrt{9,119}.sqrt{10000}

=sqrt{9,119}.sqrt{100^2}=sqrt{9,119}.100

approx 3,019.100=301,9.

(vì 9,1190 = 9,119)

+ sqrt {0,09119} =sqrt {9,119.0,01}=sqrt{9,119}.sqrt{0,01}

=sqrt{9,119}.sqrt{0,1^2}=sqrt{9,119}.0,1

approx 3,019.0,1=0,3019.

sqrt {0,0009119} =sqrt {9,119.0,0001}=sqrt{9,119}.sqrt{0,0001}

=sqrt{9,119}.sqrt{0,01^2}=sqrt{9,119}.0,01

approx 3,019.0,01=0,03019.

Bài 42 trang 23 SGK Toán 9 tập 1

Dùng bảng căn bậc hai để tìm giá trị gần đúng của nghiệm mỗi phương trình sau:

a) x^2=3,5;

b) x^2=132

Hướng dẫn giải:

a) x^2=3,5Rightarrow x=2sqrt{2,5}Rightarrow xapprox1,87

b) x^2=132Rightarrow x=sqrt{132}Rightarrow xapprox11,48

………………………..

Như vậy TaiLieuViet đã giới thiệu các bạn tài liệu Giải Toán 9 bài 5 Bảng Căn bậc hai. Để tham khảo lời giải những bài tiếp theo, mời các em vào chuyên mục Giải Toán 9 trên TaiLieuViet nhé. Chuyên mục tổng hợp lời giải theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong SGK Toán 9. Chúc các em học tốt, nếu có thắc mắc hay trao đổi kiến thức các em có thể vào link sau nhé: Hỏi – đáp

Ngoài tài liệu trên, mời các bạn tham khảo thêm tài liệu: Toán lớp 9, Ngữ văn lớp 9, Địa lý lớp 9, Tài liệu học tập lớp 9, và các đề học kì 1 lớp 9 và đề thi học kì 2 lớp 9 mới nhất được cập nhật.

Giải Toán 9 bài 5 Bảng Căn bậc haiBài tiếp theo: Giải Toán 9 bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai