tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 7: Vị trí tương đối của hai đường tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 7: Vị trí tương đối của hai đường tròn
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu hai đường tròn tiếp xúc thì tiếp điểm nằm trên đường thẳng nối tâm.
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
Lời giải:
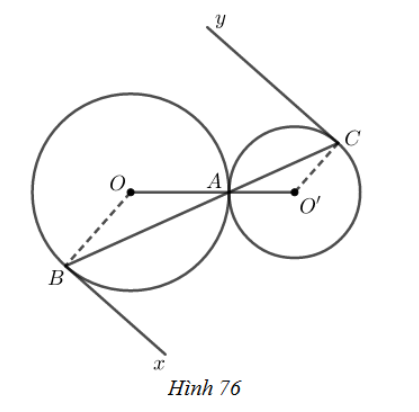
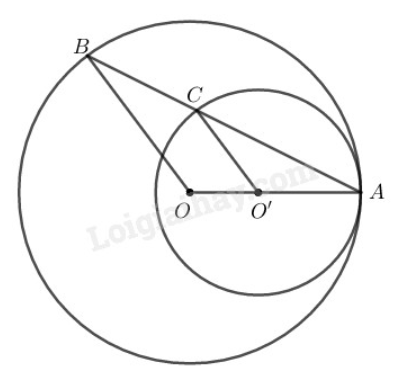
Vì hai đường tròn (O) và (O′) tiếp xúc nhau tại A.
Nên O,A,O′ thẳng hàng
Lại có C,A,B thẳng hàng
Suy ra: OAB^=O′AC^ (đối đỉnh) (1)
Tam giác AOB cân tại O (do OA=OB)
Suy ra: OAB^=OBA^ (2)
Tam giác AO′C cân tại O′ (do O′A=O′C)
Suy ra: O′AC^=O′CA^ (3)
Từ (1), (2) và (3) suy ra: OBA^=O′CA^
Suy ra OB//O′C (vì có cặp góc so le trong bằng nhau)
Lại có: Bx⊥OB (tính chất tiếp tuyến)
Suy ra: Bx⊥O′C
Mà: Cy⊥O′C ( tính chất tiếp tuyến)
Suy ra: Bx//Cy.
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.
+) Sử dụng định lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
+) Nếu OO′=R+r thì đường tròn (O) và đường tròn (O′) tiếp xúc ngoài.
Lời giải:
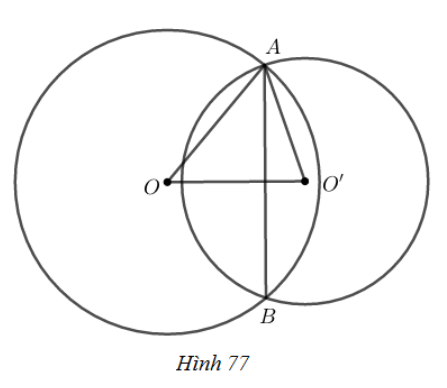
Gọi H là giao điểm của AB và OO′.
Suy ra OO′⊥AB tại H.
Vì OO′ là đường trung trực của AB (do hai đường tròn (O) và (O′) cắt nhau tại A và B) nên:
HA=HB=12AB=12.24=12(cm)
Áp dụng định lí Py−ta−go vào tam giác vuông AOH, ta có: AO2=OH2+AH2
Suy ra: OH2=OA2−AH2=152–122=81
⇒OH=9(cm)
Áp dụng định lí Py-ta-go vào tam giác vuông AO′H, ta có:AO′2=O′H2+AH2
Suy ra: O′H2=O′A2−AH2=132–122=25
⇒O′H=5(cm)
Vậy OO′=OH+O′H=9+5=14(cm).
Phương pháp giải:
Sử dụng kiến thức: Nếu một đường thẳng cắt hai đường thẳng tạo ra các góc đồng vị bằng nhau thì hai đường thẳng đó song song với nhau.
Lời giải:
Ta có: OA=OB (= bán kính đường tròn (O))
Suy ra tam giác AOB cân tại O
Hay OAB^=OBA^ (1)
Ta có: O′A=O′C (= bán kính đường tròn (O’))
Suy ra tam giác AO′C cân tại O′
Hay O′AC^=O′CA^ (2)
Từ (1) và (2) suy ra: OBA^=O′CA^
Suy ra: OB//O′C ( vì có hai góc ở vị trí đồng vị bằng nhau).
Sử dụng kiến thức: Để chứng minh ba điểm thẳng hàng ta có thể chứng minh qua ba điểm đó xác định góc bẹt (góc180o)
Lời giải:
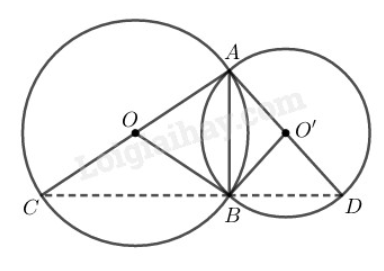
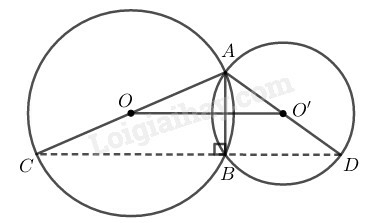
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên ABC^=90∘
Tam giác ABD nội tiếp trong đường tròn (O′) có AD là đường kính nên ABD^=90∘
Ta có: CBD^=ABC^+ABD^=90∘+90∘=180∘
Vậy ba điểm C,B,D thẳng hàng và AB⊥CD (vì ABC^=90∘
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Lời giải:
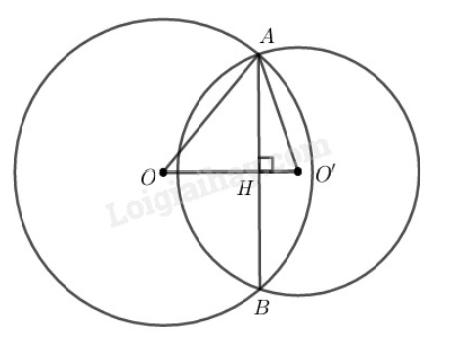
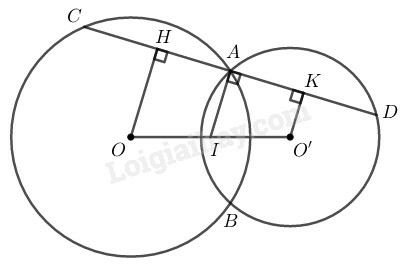
Kẻ OH⊥CD,O′K⊥CD
Ta có: IA⊥CD
Suy ra: OH//IA//O′K
Theo giả thiết: IO=IO′
Suy ra: AH=AK (1) (tính chất đường thẳng song song cách đều)
Xét đường tròn (O) có OH⊥AC mà OH là 1 phần đường kính và AC là dây cung
Suy ra: HA=HC=12AC (quan hệ giữa đường kính và dây cung)
⇒AC=2AH(2)
Xét đường tròn (O’) có O′K⊥AD mà O’K là 1 phần đường kính và AD là dây cung
Suy ra: KA=KD=12AD ( quan hệ giữa đường kính và dây cung)
⇒AD=2AK(3)
Từ (1),(2) và (3) suy ra: AC=AD.
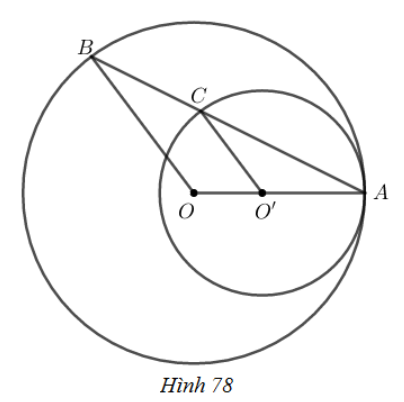
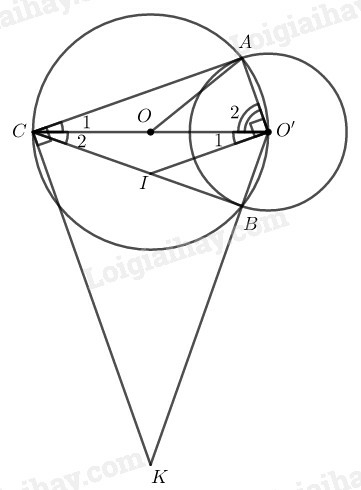
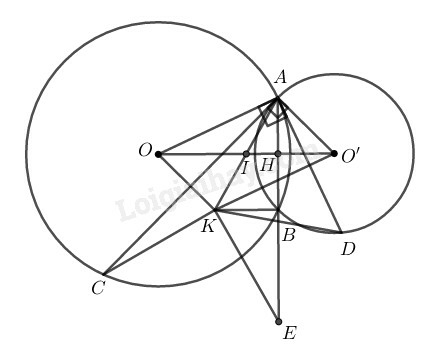
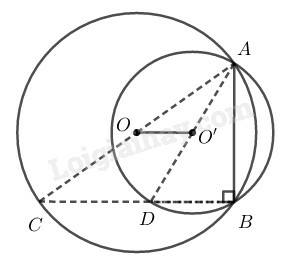
a) Chứng minh rằng CA,CB là các tiếp tuyến của đường tròn (O′)
b) Đường vuông góc với AO′ tại O′ cắt CB ở I. Đường vuông góc với AC tại C cắt đường thẳng O′B ở K. Chứng minh rằng ba điểm O,I,K thẳng hàng.
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
+) Để chứng minh ba điểm thẳng hàng ta có thể dùng tính chất đường trung trực: chứng minh ba điểm đó cùng cách đều hai đầu mút đoạn thẳng.
Lời giải:
a) Tam giác AO′C nội tiếp trong đường tròn (O) có O′C là đường kính nên O′AC^=90∘
Suy ra: CA⊥O′A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O′)
Tam giác BO′C nội tiếp trong đường tròn (O) có O′C là đường kính nên O′BC^=90∘
Suy ra: CB⊥O′B tại điểm B
Vậy CB là tiếp tuyến đường tròn (O′)
b) Trong đường tròn (O′) ta có AC và BC là hai tiếp tuyến cắt nhau tại C.
Suy ra: AO′C^=BO′C^ và ACO′^=BCO′^ (tính chất hai tiếp tuyến cắt nhau)
Mà O′I⊥O′A (gt)
CA⊥O′A (chứng minh trên)
Suy ra: O′I//CA ⇒ACO′^=CO′I^ (hai góc so le trong)
Suy ra: BCO′^=CO′I^
Hay tam giác CIO′ cân tại I⇒IC=IO′
Khi đó I nằm trên đường trung trực của O′C
Lại có: AO′C^=BO′C^ (chứng minh trên)
KC⊥CA(gt)
O′A⊥AC (chứng minh trên)
Suy ra:KC//O′A ⇒AO′C^=O′CK^ (hai góc so le trong)
Suy ra: O′CK^=KO′C^
Hay tam giác CKO′ cân tại K⇒KC=KO′
Khi đó K nằm trên đường trung trực của O′C
Mặt khác: OC=OO′ (= bán kính đường tròn (O))
Suy ra O,I,K nằm trên đường trung trực của O′C.
Vậy O,I,K thẳng hàng.
a) AB⊥KB;
b) Bốn điểm A,C,E,D nằm trên cùng một đường tròn.
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là trung trực của dây chung.
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Hai điểm gọi là đối xứng với nhau qua O nếu O là trung điểm của đoạn thẳng nối hai điểm đó
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Để chứng minh các điểm cùng thuộc một đường tròn, ta chứng minh chúng cùng cách đều một điểm.
Lời giải:
a) Gọi H là giao điểm của AB và OO′.
Vì hai đường tròn (O) và (O′) cắt nhau tại A và B nên OO′ là đường trung trực của AB
Hay OO′⊥AB tại H và HA=HB
Lại có I là trung điểm của OO′ nên IH⊥AB(1)
Trong tam giác ABK, ta có:
HA=HB (chứng minh trên)
IA=IK (tính chất đối xứng tâm)
Suy ra IH là đường trung bình của tam giác ABK
Suy ra IH//BK(2)
Từ (1) và (2) suy ra: AB⊥KB
b) Vì AB⊥KB nên AE⊥KB
Lại có: AB=BE ( tính chất đối xứng tâm)
Suy ra KB là đường trung trực của AE
Do đó: KA=KE ( tính chất đường trung trực) (3)
Ta có: IO=IO′(gt)
IA=IK ( chứng minh trên)
Tứ giác AOKO′ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Suy ra: OK//O′A và OA//O′K
CA⊥O′A (vì CA là tiếp tuyến của đường tròn (O′))
OK//O′A ( chứng minh trên)
Suy ra: OK⊥AC
Xét đường tròn (O) có OK⊥AC mà OK là 1 phần đường kính và AC là dây cung nên OK đi qua trung điểm của AC.
Khi đó OK là đường trung trực của AC
Suy ra: KA=KC ( tính chất đường trung trực) (4)
DA⊥OA ( vì DA là tiếp tuyến của đường tròn (O))
O′K//OA ( chứng minh trên)
Suy ra: O′K⊥DA
Xét đường tròn (O’) có O′K⊥DA mà O’K là 1 phần đường kính và AD là dây cung nên O’K đi qua trung điểm của AD.
Khi đó O′K là đường trung trực của AD
Suy ra: KA=KD ( tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA=KC=KE=KD
Vậy bốn điểm A,C,E,D cùng nằm trên một đường tròn.
Bài tập bổ sung (trang 168 SBT Toán 9)
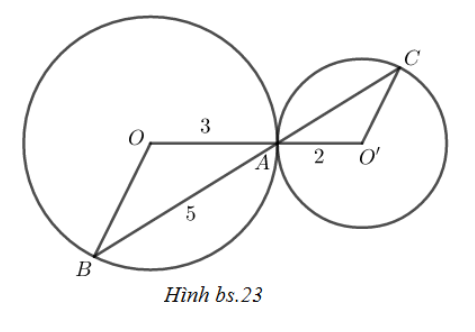
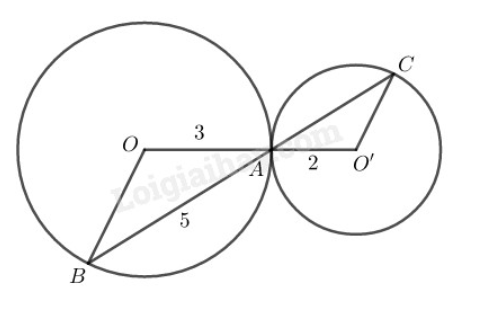
(A) 103 ; (B) 3,5 ;
(C) 3 ; (D) 4.
Hãy chọn phương án đúng.
Phương pháp giải:
Quy về xét hai tam giác đồng dạng theo trường hợp góc – góc
Lời giải:
Ta có: ΔOAB cân tại O (do OA=OB) nên OBA^=OAB^
ΔO′AC cân tại O’ (do O′A=O′C) nên O′CA^=O′AC^
Mà OAB^=O′AC^ (đối đỉnh)
⇒OBA^=OAB^=O′AB^=O′AC^
Nên ΔOAB∽ΔO′AC(g.g)
⇒OAO′A=ABAC
⇒AC=AB.O′AOA=5.23=103
Vậy chọn (A).
Sử dụng kiến thức:
+) Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
Vì ABC^=90∘ nên tam giác ABC vuông tại B có O là tâm đường tròn ngoại tiếp, do đó A,O,C thẳng hàng.
Vì ABD^=90∘ nên tam giác ABD vuông tại B có O’ là tâm đường tròn ngoại tiếp, do đó A,O′,D thẳng hàng.
Trong ∆ACD, có:
O là trung điểm của AC
O′ là trung điểm của AD
⇒OO′ là đường trung bình của ∆ACD nên OO′=12CD.
Chú ý: 2 trường hợp hình vẽ đều được chứng minh như trên.
