tailieuviet.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Phương pháp giải:
Sử dụng:
– Diện tích xung quanh của hình nón: Sxq=πrl.
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, l là đường sinh, h là chiều cao)..
Lời giải:
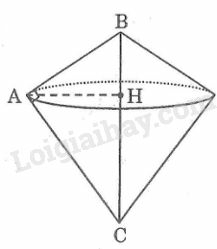
Khi quay tam giác vuông ABC một vòng xung quanh cạnh huyền BC ta thu được hai hình nón có đáy úp vào nhau, bán kính đường tròn đáy bằng đường cao AH kẻ từ A đến cạnh huyền BC.
Trong tam giác vuông ABC ta có:
+) AB=BC.cosB=2a.cos60o=2a.12=a
+) AC=BC.sinB=2a.sin60o=2a.32=a3
+) AB.AC=AH.BC (hệ thức lượng trong tam giác vuông)
⇒AH=AB.ACBC=a.a32a=a32
Diện tích xung quanh hình tạo thành là:
S=π.AH.AB+πAH.AC=π.AH.(AB+AC)
=π.a32(a+a3)=πa2(3+3)2 (đơn vị diện tích)
Thể tích hình tạo thành là:
V=13πAH2.BH+13πAH2.HC=13πAH2.(BH+HC)
V=13πAH2.BC=13π(a32)2.2a=13π.a2.34.2a=πa32.
Phương pháp giải:
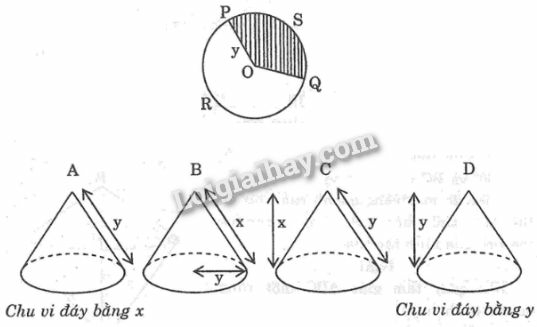
Quan sát hình vẽ để tưởng tượng hình nón tạo thành từ phần hình quạt còn lại sau khi cắt.
Lời giải:
Phần còn lại ghép thành hình nón sẽ có đường sinh là y; chu vi đáy là độ dài của PRQ⏜ là x.
Chọn hình A.
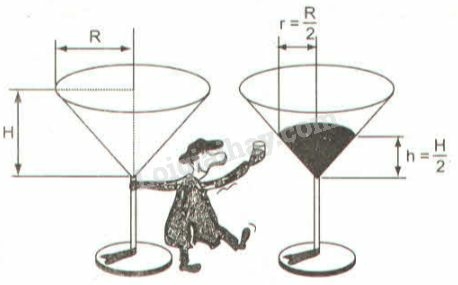
Cụ Bá uống một lượng rượu nên “chiều cao” của rượu còn lại trong cốc bằng một nửa chiều cao ban đầu.
Hỏi cụ Bá đã uống bao nhiêu phần rượu trong cốc?
Phương pháp giải:
Sử dụng:
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
Lời giải:
Thể tích rượu ban đầu trong cốc là: V1=13πR2.H
Thể tích rượu còn lại trong cốc là: V2=13πr2.h=13π(R2)2.H2=124πR2H=18.13πR2H=18V1
Thể tích rượu đã uống là: V1−V2=V1−18V1=78V1
Vậy cụ Bá đã uống 78 thể tích rượu trong cốc.
Thể tích nước chứa đầy xô sẽ là (tính theo cm3):
(A) 1000π3; (B) 1750π3;
(C) 2000π3; (D) 2750π3.
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
Lời giải:
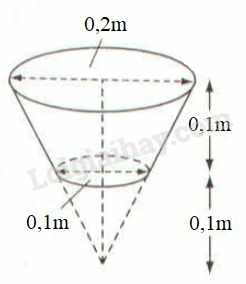
Thể tích hình nón có đường kính đáy 0,2m là:
13π.(0,22)2.0,2=0,002π3(m3)=2000π3(cm3)
Thể tích hình nón có đường kính đáy 0,1m là:
13π.(0,12)2.0,1=0,00025π3(m3)=250π3(cm3)
Thể tích nước chứa đầy xô là:
V=2000π3−250π3=1750π3(cm3)
Chọn (B).
(A) 220; (B) 264;
(C) 308; (D) 374.
(Chọn π=227 và tính gần đúng đến cm2).
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Diện tích xung quanh của hình nón: Sxq=πrl.
– Diện tích toàn phần của hình nón: Stp=Sxq+Sđ=πrl+πr2.
(r là bán kính đường tròn đáy, l là đường sinh).
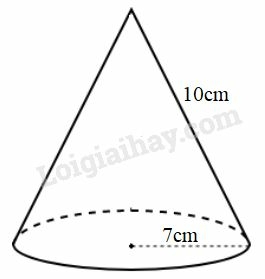
Lời giải:
Diện tích xung quanh hình nón là:
Sxq=πrl=227.7.10=220(cm2)
Diện tích đáy hình nón là:
Sđ=πr2=227.72=154(cm2)
STP=Sxq+Sđ=220+154=374(cm2).
Chọn (D).
a) Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần S1 của hình tạo thành khi quay quanh cạnh AD.
b) Xác định giá trị x khi S=S1 và S=2S1.
Phương pháp giải:
Sử dụng:
– Diện tích xung quanh của hình nón: Sxq=πrl.
(r là bán kính đường tròn đáy, l là đường sinh).
– Diện tích xung quanh hình trụ: Sxq=2πrh.
(r là bán kính đường tròn đáy, h là chiều cao).
Lời giải:
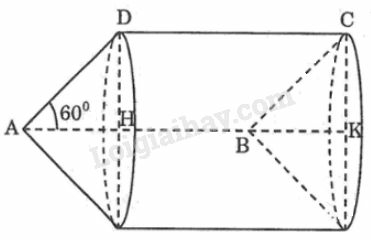
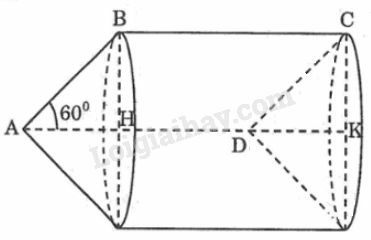
a) Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên 2 hình nón bằng nhau có đường sinh AD=BC=x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính đáy hình nón.
Trong ∆AHD có AHD^=90∘;A^=60∘, ta có:
DH=AD.sin60o=x.32=x32
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh 2 hình nón và diện tích xung quanh hình trụ: S=Sxq trụ+2Sxq nón
S=2πDH.DC+2.πDH.AD=2πx32.1+2.π.x32.x=πx3+πx23
⇒S=πx3(1+x)
Khi quay hình bình hành quanh trục AD một vòng thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB=CD=1. Cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy hình nón.
Bán kính đáy: BH=AB.sin60o=1.32=32
S1 là diện tích toàn phần hình tạo thành bằng tổng diện tích xung quanh hai hình nón cộng với diện tích hình trụ.
S1=Sxq trụ+2Sxq nón
S1=2π.BH.BC+2.π.BH.AB
S1=2π.32.x+2.π.32.1
S1=π3(x+1)
b) Để S=S1 ⇔πx3(1+x)=π3(x+1)
⇔x(1+x)=x+1
⇔x(x+1)−(x+1)=0
⇔(x+1)(x−1)=0
Vì x>0⇒x+1≠0
⇒x−1=0⇔x=1
Vậy x=1 thì S=S1.
Để S=2S1 ⇔πx3(1+x)=2π3(x+1)
⇔x(x+1)=2(x+1)
⇔x(x+1)−2(x+1)=0
⇔(x+1)(x−2)=0
Vì x>0⇒x+1≠0
⇒x−2=0⇔x=2.
Vậy x=2 thì S=2S1.
Người ta múc đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là:
(A) l6(cm); (B) l(cm);
(C) 56 (cm); (D) 116l (cm).
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
– Thể tích hình trụ: V=Sh=πr2h.
(r là bán kính đường tròn đáy, h là chiều cao, S là diện tích đáy).
Lời giải:
Thể tích hình nón là: V1=13πr2.h
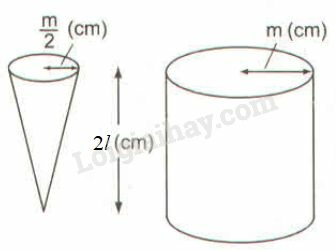
V1=13π(m2)2.2l=13πm24.2l=πm2l6 (cm3)
Thể tích hình trụ là: V2=πr2.h
V2=πm2.2l=2πm2l (cm3)
V1V2=πm2l6:2πm2l=πm2l6.12πm2l=112
Vậy khi đổ đầy nước vào hình nón rồi đổ vào hình trụ thì độ cao của nước trong hình trụ là 112.2l=16l (cm).
Chọn (A).
(A) 54; (B) 1512;
(C) 2516; (D) 12564.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
Lời giải:
Gọi bán kính đáy hình nón ban đầu là r, độ dài đường cao là h.
Thể tích hình nón ban đầu là: V=13πr2.h
Thể tích nón mới khi bán kính và chiều cao tăng là:
V1=π(54r)2.54h=πr2.h.(54)3
V1V=13πr2h.(54)313πr2h=(54)3=12564
Chọn (D).
Sử dụng:
– Công thức tính thể tích hình trụ: V=Sh=πr2h.
(r là bán kính đường tròn đáy, h là chiều cao, S là diện tích đáy).
Lời giải:
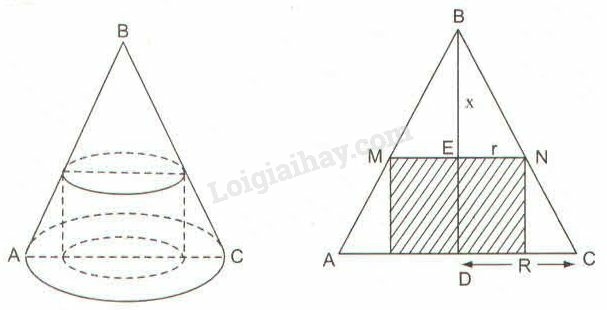
Gọi bán kính đáy hình nón là R, chiều cao hình nón là h, bán kính đáy hình trụ là r, chiều cao phần hình nón cắt đi là BE=x.
Vì MN//AC, theo hệ quả định lí Ta-lét ta có:
MEAD=BEBD hay rR=xh⇒r=Rxh
Thể tích hình trụ là: V=πr2.(h−x)
V=π.(Rxh)2.(h−x)=π.R2x2h2.(h−x)
Phần bỏ đi của hình nón ít nhất có nghĩa là thể tích của hình trụ lớn nhất:
V=π.R2x2h2(h−x)
⇒2Vh2=πR2x2(2h−2x)
⇒2Vh2πR2=x2(2h−2x))
Vì π,R,h là các hằng số nên thể tích hình trụ lớn nhất khi và chỉ khi x2(2h−2x) lớn nhất. Ta có x2(2h−2x)=x.x.(2h−2x)
Áp dụng bất đẳng thức Cô – si cho ba số dương x,x,2h−2x ta có:
x.x.(2h−2x)3≤x+x+2h−2×3=2h3 ⇒x.x.(2h−2x)≤(2h3)3 =8h327
Dấu “=” xảy ra khi x=2h−2x⇔3x=2h ⇒x=23h
Vậy khi phần cắt bỏ ở phía trên hình nón có chiều cao bằng 23 chiều cao hình nón thì phần bỏ đi là ít nhất.
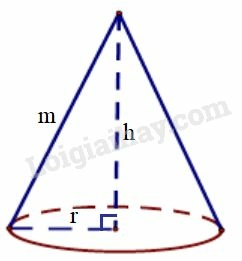
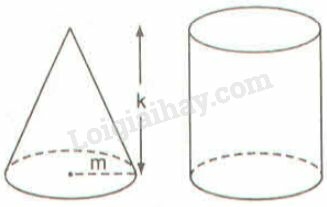
Chiều cao là h(cm), bán kính đường tròn đáy là r(cm) và độ dài đường sinh m(cm) thì thể tích hình nón này là:
(A) πr2h(cm3);
(B) 13πr2h(cm3);
(C) πrm(cm3);
(D) πr(r+m)(cm3).
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
Lời giải:
Chiều cao hình nón là h(cm), bán kính đường tròn đáy là r(cm), độ dài đường sinh là m(cm).
Thể tích hình nón là: V=13πr2.h(cm3).
Chọn (B).
(A) 2π3(cm3); (B) 4π3(cm3);
(C) 2π(cm3); (D) 8π3(cm3).
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Thể tích hình trụ: V=Sh=πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
Lời giải:
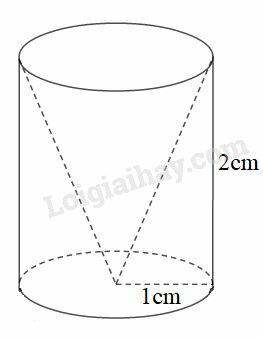
Thể tích hình trụ là: V1=πr2.h=π.12.2=2π(cm3)
Thể tích hình nón là: V2=13πr2.h=13π.12.2=23π(cm3)
Thể tích phần còn lại của hình trụ là: V=V1−V2=2π−23π=43π(cm3)
Chọn (B).
1V12=1V22+1V32.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
– Định lí Pytago trong tam giác vuông: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải:
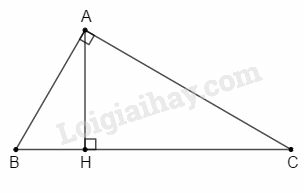
∆ABC có A^=90∘, đặt AB=c,AC=b,BC=a,AH=h; AH là đường cao kẻ từ đỉnh A đến cạnh huyền BC.
Ta có: h=bca (hệ thức lượng trong tam giác vuông)
– Khi quay tam giác vuông ABC quanh cạnh huyền BC một vòng thì cạnh AB và AC vạch nên hai hình nón có chung đáy có bán kính đáy bằng đường cao AH và tổng chiều cao 2 hình nón bằng cạnh huyền BC. Như vậy, thể tích hình sinh ra là:
V1=13π.AH2.HB+13π.AH2.HC
=13AH2.(HB+HC)
=13AH2.BC
=13π(bca)2.a=πb2c23a
⇒1V12=1(πb2c23a)2=9a2π2b4c4 (1)
– Khi quay ∆ABC quanh cạnh AB một vòng ta thu được hình nón có chiều cao AB=c, bán kính đáy AC=b và thể tích hình sinh ra là:
V2=13π.AC2.AB=13πb2c
⇒1V22=1(πb2c3)2=9π2b4c2
– Khi quay ∆ABC quanh cạnh AC một vòng ta thu được hình nón có chiều cao AC=b, bán kính đáy AB=c và thể tích hình sinh ra là:
V3=13AB2.AC=13πc2b
⇒1V32=1(πbc23)2=9π2b2c4
Ta có:
1V22+1V32=9π2b4c2+9π2b2c4=9(b2+c2)π2b4c4
Áp dụng định lí Pytago vào ∆ABC vuông tại A, ta có:
b2+c2=a2
⇒1V22+1V32=9(b2+c2)π2b4c4=9a2π2b4c4 (2)
Từ (1) và (2) suy ra: 1V12=1V22+1V32.
Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là:
(A) k4cm; (B) k3cm;
(C) 2k3cm; (D) 3k4cm.
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
– Thể tích hình nón: V=13πr2h.
(r là bán kính đường tròn đáy, h là chiều cao).
– Thể tích hình trụ: V=Sh=πr2h.
(r là bán kính đường tròn đáy, h là chiều cao, S là diện tích đáy).
Lời giải:
Vnón=13πm2.kVtrụ=πm2.k⇒Vtrụ=3Vnón
Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ bằng 13 độ cao của hình trụ tức là k3cm.
Chọn (B).
