Chuyên đề Toán học lớp 9: Giải bài toán bằng cách lập hệ phương trìnhđược TaiLieuViet sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Đây là tài liệu hay giúp các bạn củng cố kiến thức, đồng thời học tốt môn Toán học lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

I. Các bước giải Toán

Để giải bài toán bằng cách lập phương trình, hệ phương trình ta thường thực hiện theo các bước sau:

+ Bước 1: Chọn ẩn số (nêu đơn vị của ẩn và đặt điều kiện nếu cần).

+ Bước 2: Tính các đại lượng trong bài toán theo giả thiết và ẩn số, từ đó lập phương trình hoặc hệ phương trình.

+ Bước 3: Giải phương trình hoặc hệ phương trình vừa lập.

+ Bước 4: Đối chiếu với điều kiện và trả lời.

II. Một số kiến thức cần nhớ

1. Các bài toán chuyển động

Kiến thức cần nhớ:

+ Quãng đường = Vận tốc. Thời gian.

+ Vận tốc tỷ lệ nghịch với thời gian và tỷ lệ thuận với quãng đường đi được:

+ Nếu hai xe đi ngược chiều nhau khi gặp nhau lần đầu: Thời gian hai xe đi được là như nhau, Tổng quãng đường 2 xe đi được bằng đúng quãng đường cần đi của 2 xe.

+ Nếu hai phương tiện chuyển động cùng chiều từ hai địa điểm khác nhau là A và B, xe từ A chuyển động nhanh hơn xe từ B thì khi xe từ A đuổi kịp xe từ B ta luôn có hiệu quãng đường đi được của xe từ A với quãng đường đi được của xe từ B bằng quãng đường AB

+ Đối với (Ca nô, tàu xuồng) chuyển động trên dòng nước: Ta cần chú ý:

Khi đi xuôi dòng: Vận tốc ca nô = Vận tốc riêng + Vận tốc dòng nước.

Khi đi ngược dòng: Vận tốc ca nô = Vận tốc riêng – Vận tốc dòng nước.

Vận tốc của dòng nước là vận tốc của một vật trôi tự nhiên theo dòng nước (Vận tốc riêng của vật đó bằng 0)

2. Bài toán liên quan đến năng suất lao động, công việc.

Ta cần chú ý: Khi giải các bài toán liên quan đến năng suất thì liên hệ giữa ba đại lượng là: Khối lượng công việc = năng suất lao động × thời gian

III. Ví dụ cụ thể

Câu 1:Một người đi xe đạp từ A đến B cách nhau 24km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4km/h so với lúc đi, nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A đến B.

Hướng dẫn:

Đổi 30 phút = 1/2 giờ.

Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x > 0). Thời gian xe đi từ A đến B là 24/x (giờ).

Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là Lý thuyết: Giải bài toán bằng cách lập hệ phương trình (giờ)

Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:

Lý thuyết: Giải bài toán bằng cách lập hệ phương trình

Giải phương trình:

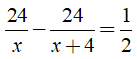
Lý thuyết: Giải bài toán bằng cách lập hệ phương trình

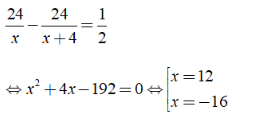
Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.

Cách 1: Lập hệ phương trình

Gọi thời gian vòi một chảy một mình đầy bể trong x (giờ, x > 24/5 )

Gọi thời gian vòi hai chảy một mình đầy bể trong y (giờ, y > 24/5 )

Biết hai vòi cùng chảy thì sau 24/5 giờ thì đầy bể nên ta có phương trình: Lý thuyết: Giải bài toán bằng cách lập hệ phương trình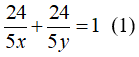

Nếu chảy riêng thì vòi một chảy đầy bể nhanh hơn vòi hai là 4 giờ nên ta có phương trình:

x = y – 4 (2)

Từ (1) và (2) ta có hệ phương trình:

Lý thuyết: Giải bài toán bằng cách lập hệ phương trình

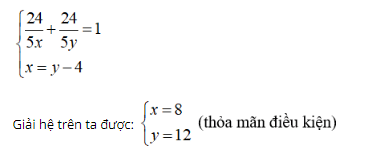
Vậy vòi một chảy một mình trong 8 giờ thì đầy bể và vòi hai chảy một mình trong 12 giờ thì đầy bể.

IV. Bài tập tự luyện

Mộ số bài Toán bằng cách lập hệ phương trình cho các bạn học sinh tự luyện

Giải bài toán bằng cách lập hệ phương trình

Giải bài toán bằng cách lập hệ phương trình

Câu 45 trang 14 Sách bài tập (SBT) Toán 9 tập 2

Hai công nhân cùng sơn cửa cho một công trình trong bốn ngày thì xong việc) Nếu người thứ nhất làm một mình trong chín ngày rồi người thứ hai đến cùng làm tiếp trong một ngày nữa thì xong việc). Hỏi mỗi người làm một mình thì bao lâu xong việc?

Gọi thời gian người thứ nhất làm riêng xong công việc là x ngày

Người thứ hai làm riêng xong công việc là y ngày

Điều kiện: x > 4; y > 4

Trong 1 ngày người thứ nhất làm được frac{1}{x} công việc

Trong 1 ngày người thứ hai làm được frac{1}{y} công việc

Trong 1 ngày cả hai người làm được 1:4=frac{1}{4} công việc

Ta có phương trình: frac{1}{x}+frac{1}{y}=frac{1}{4}

Người thứ nhất làm riêng 9 ngày, người thứ hai đến làm chung 1 ngày nữa thì xong, ta có phương trình:

frac{10}{x}+frac{1}{y}=1

Ta có hệ phương trình:

Giải bài toán bằng cách lập hệ phương trình

x = 12; y = 6 thỏa mãn điều kiện bài toán.

Vậy: Người thứ nhất làm riêng xong công việc trong 12 ngày

Người thứ hai làm riêng xong công việc trong 6 ngày.

Giải bài toán bằng cách lập hệ phương trình được TaiLieuViet chia sẻ trên là tài liệu khá hay, bao gồm các chuyên đề gồm phần lý thuyết có bài tập kèm theo giúp học sinh vận dụng giải bài tập một cách dễ dàng. Hơn nữa tài liệu này hệ thống lại toàn bộ kiến thức cách lập hệ phương trình giúp học sinh ôn tập một cách thuận tiện hơn. Chúc các bạn học tốt, mời các bạn tham khảo

  • Giải hệ phương trình bằng phương pháp cộng đại số
  • Giải hệ phương trình bằng phương pháp thế
  • Chuyên đề Hệ phương trình ôn thi vào lớp 10
  • Phương trình quy về phương trình bậc hai

Trên đây TaiLieuViet đã giới thiệu tới các bạn Giải bài toán bằng cách lập hệ phương trình. Để có kết quả cao hơn trong học tập, TaiLieuViet xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 9, Giải bài tập Toán lớp 9 mà TaiLieuViet tổng hợp và giới thiệu tới các bạn đọc