Bộ Đề thi vào lớp 10 môn Toán TP.HCM năm 2023 có đáp án 

tailieuviet.vn xin giới thiệu Bộ Đề thi vào lớp 10 môn Toán TP.HCM năm 2023 có đáp án. Mời các bạn đón xem:

Chỉ 100k mua trọn Bộ Đề thi vào lớp 10 môn Toán TP.HCM năm 2023 có đáp án bản word có lời giải chi tiết (chỉ 20k cho 1 đề thi bất kì):

B1: Gửi phí vào tài khoản 0711000255837 – NGUYEN THANH TUYEN – Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Bộ Đề thi vào lớp 10 môn Toán TP.HCM năm 2022 có đáp án

Sở Giáo dục và Đào tạo TP.HCM

Kì thi tuyển sinh vào lớp 10

Năm học 2022

Môn thi: Toán (hệ Công lập)

Thời gian làm bài: 120 phút

Bài 1. (1,5 điểm)

Cho parabol (P):y=x2 và đường thẳng .

a) Vẽ (P)  và  (d)  trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm (P) và (d)  bằng phép tính.

Bài 2. (1,0 điểm)     

Cho phương trình x2-4⁢x-3=0  có hai nghiệm là x1,x2 .

Không giải phương trình, hãy tính giá trị của biểu thức A=(x1-x2)2 .

Bài 3. (1,0 điểm)

Để đánh giá thể trạng (gầy, bình thường, thừa cân) của một người, người ta thường dùng chỉ số BMI (Body Mass Index). Chỉ số BMI được tính dựa trên chiều cao và cân nặng theo công thức sau:

BMI(kg/m2)=c⁢â⁢n⁢nng⁢(kg)chi⁢ê⁢u⁢cao⁢(m)×chi⁢ê⁢u⁢cao⁢(m).

Đối với người trưởng thành, chỉ số này được đánh giá như sau: 

HHạnh và Phúc là hai người trưởng thành đang cần xác định thể trạng của mình.

a) Hạnh cân nặng 50 kg và cao 1,63 m. Hãy cho biết phân loại theo chỉ số BMI của Hạnh?

b) Phúc cao 1,73 m thì cân nặng trong khoảng nào để chỉ số BMI của Phúc ở mức bình thường ? (làm tròn kết quả đến chữ số thập phân thứ nhất)

Bài 4. (0,75 điểm)

          Giá bán một cái bánh cùng loại ở hai cửa hàng A và B  đều là 15 000 đồng, nhưng mỗi cửa hàng áp dụng hình thức khuyến mãi khác nhau.

          Cửa hàng A: đối với 3 cái bánh đầu tiên, giá mỗi cái là 15 000 đồng và từ cái bánh thứ tư trở đi, khách hàng chỉ phải trả 75% giá bánh.

          Cửa hàng B: cứ mua 3 cái bánh được tặng thêm 1 cái bánh cùng loại.

Bạn Hằng cần đúng 13 cái bánh để tổ chức sinh nhật thì bạn ấy nên mua bánh ở cửa hàng nào để tiết kiệm và tiết kiệm được bao nhiêu tiền so với cửa hàng kia?

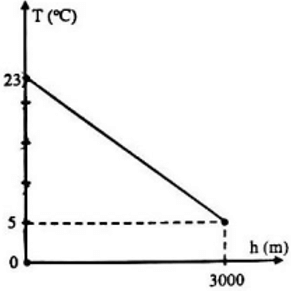
Một vận động viên khi leo núi nhận thấy rằng càng lên cao thì nhiệt độ không khí càng giảm. Mối liên hệ giữa nhiệt độ không khí T  và độ cao h  (so với chân núi) được cho bởi hàm số T=a.h + b  có đồ thị như hình vẽ bên (nhiệt độ T  tính theo C∘  và độ cao h  tính theo mét) Tại chân núi, người đó đo được nhiệt độ không khí là 23∘⁢C và trung bình cứ lên cao 100 m thì nhiệt độ giảm 0,6∘⁢C. a) Xác định a,b  trong công thức trên. b) Bạn Minh đang leo núi và dùng nhiệt kế đo được nhiệt độ không khí tại vị trí dừng chân là 23∘⁢C .  Hỏi bạn Minh đang ở độ cao bao nhiêu mét so với chân núi ?

Bài 6. (1,0 điểm)

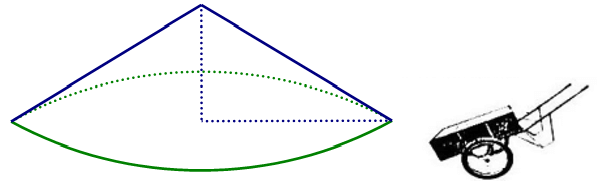
Một đống cát có dạng hình nón có chu vi đáy là 25,12 m và độ cao là 1,5 m.

a) Tính thể tích của đống cát trên ? Biết công thức tính chu vi đường tròn là C=2⁢π⁢R > và công thức tính thể tích hình nón là V=13⁢π⁢R2⁢h  (trong đó R là bán kính đường tròn đáy; h là chiều cao hình nón, lấy π=3,14) .

b) Người ta dùng xe cải tiến để vận chuyển đống cát đó đên khu xây dựng. Biết thùng chứa của xe cải tiến có dạng hình hộp chữ nhật có kích thước dài 1 m, rộng 6 dm và cao 3 dm. Trong mỗi chuyến xe, thùng xe có thể chứa nhiều hơn thể tích thực của nó là 10% để vận chuyển được nhiểu cát hơn. Hỏi cần ít nhất bao nhiêu chuyến xe cải tiến để chuyển hết đống cát trên?

Bài 7. (0,75 điểm)

          Đại hội Thể thao Đông Nam Á – SEA Games (South East Asian Games) là sự kiện thể thao được tổ chức 2 năm một lần với sự tham gia của các vận động viên trong khu vực Đông Nam Á. Việt Nam là chủ nhà của SEA Games 31 diễn ra từ này 12/5/2022 đến ngày 23/5/2022.

          Ở môn bóng đá nam, một bảng đấu gồm có 5 đội A, B, C, D, E thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại). Trong mỗi trận đấu, đội thắng được 3 điểm, đội hòa được 1 điểm và đội thua được 0 điểm.

a) Hỏi có tất cả bao nhiêu trận đấu đã diễn ra ở bảng đấu trên?

b) Khi kết thúc bảng đấu, các đội A, B, C, D, E lần lượt có điểm số là 10, 9, 6, 4, 0. Hỏi có bao nhiêu trận hòa và cho biết đó là trận hòa giữa các đội nào (nếu có)?

Bài 8. (3,0 điểm)

Cho tam giác ABC  có ba góc nhọn nội tiếp đường tròn (O)(AB<AC) . Gọi D là điểm trên cung nhỏ BC sao cho DB < DC .  Từ D  kẻ DE  vuông góc với BC  ( E thuộc BC  kẻ DF  vuông góc với AC (F∈A⁢C). Đường thẳng EF  cắt tia AB  tại K .

a) Chứng minh tứ giác CDEF  nội tiếp và D⁢F⁢E^=D⁢A⁢B^ .

b) Chứng minh tứ giác DKBE  nội tiếp và DB.DF = DA.DE.

c) Gọi I,J   lần lượt là trung điểm của AB , EF Chứng minh IJ vuông góc với DJ .

–HẾT–

Bộ Đề thi vào lớp 10 môn Toán TP.HCM năm 2021 có đáp án

Sở Giáo dục và Đào tạo TP.HCM

Kì thi tuyển sinh vào lớp 10

Năm học 2021

Môn thi: Toán (hệ Công lập)

Thời gian làm bài: 120 phút

Bài 1. (1,5 điểm)

Cho parabol (P) : y=14⁢x2  và đường thẳng (d):y=-12⁢x+2 .

a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Bài 2. (1,0 điểm)

Cho phương trình: 2⁢x2-5⁢x-3=0  có hai nghiệm là x1,x2 .

Không giải phương trình, hãy tính giá trị của biểu thức: A=(x1+2⁢x2)⁢(x2+2⁢x1) .

Bài 3. (0,75 điểm)

Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó.

Để xác định CAN, ta tìm số dư r trong phép chia X cho 10 và tra vào bảng 1.

Để xác định CHI, ta tìm số dư s trong phép chia X cho 12 và tra vào bảng 2.

Ví dụ: năm 2020 có CAN là Canh, CHI là Tí.

Bảng 1

Bảng 2

a) Em hãy sữ dụng quy tắc trên để xác định CAN, CHI của năm 2005?

b) Bạn Hằng nhớ rằng Nguyễn Huệ lên ngôi hoàng đế, hiệu là Quang Trung vào năm Mậu Thân nhưng không nhớ rõ đó là năm bao nhiêu mà chỉ nhớ là sự kiện trên xảy ra vào cuối thế kỉ 18. Em hãy giúp Hằng xác định chính xác năm đó là năm bao nhiêu?

Bài 4. (0,75 điểm)

Cước điện thoại y (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả hàng tháng, nó phục thuộc vào lượng thời gian gọi x (phút) của người đó trong tháng. Mỗi liên hệ giữa hai đại lượng này là một là số bậc nhất y =ax + b. Hãy tìm a, b biết rằng nhà bạn Nam trong tháng 5 đã gọi 100 phút với số tiền là 40 nghìn đồng và trong tháng 6 gọi 40 phút với số tiền là 28 nghìn đồng.

Bài 5. (1,0 điểm)

Theo quy định của cửa hàng xe máy, đề hoàn thành chỉ tiêu trong một tháng, mỗi nhân viên phải bán được trung bình một chiếc xe máy trong một ngày. Nhân viên nào hoàn thành chỉ tiêu trong một tháng thì nhận lương cơ bản là 8 000 000 đồng.

Nếu trong một tháng nhân viên nào vượt chỉ tiêu thì được thưởng thêm 8% tiền lời của số xe được bán vượt chỉ tiêu đó. Trong tháng 5 (có 31 ngày), anh Thành nhận được số tiền là 9 800 000 đồng (bao gồm cả lương cơ bản và tiền thưởng thêm tháng đó). Hỏi anh Thành đã bán được bao nhiêu chiếc xe máy trong tháng 5, biết rằng mỗi xe máy bán ra thì cửa hàng thu lời được 2 500 000 đồng.

Bài 6. (1,0 điểm)

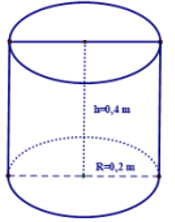
Anh Minh vừa mới xây một cái hồ trữ nước cạnh nhà có hình dạng hộp chữ nhật kích thước 2 m × 2 m × 1 m. Hiện hồ chưa có nước nên anh Minh phải ra sông lấy nước. Mỗi lần ra sông anh gánh được 1 đôi nước đầy gồm 2 thùng hình trụ bằng nhau có bán kính đáy 0,2 m, chiều cao 0,4 m.

a) Tính lượng nước (m³) anh Minh đổ vào hồ sau mỗi lần gánh (ghi kết quả làm tròn đến 2 chữ số thập phân). Biết trong quá trình gánh nước về thì lượng nước bị hao hụt khoảng 10% và công thức tính thể tích hình trụ là V=π⁢R2⁢h.

b) Hỏi anh Minh phải gánh ít nhất bao nhiêu lần để đầy hồ? Bỏ qua thể tích thành hồ.

Anh Minh vừa mới xây một cái hồ trữ nước cạnh nhà có hình dạng hộp chữ nhật kích thước 2 m × 2 m × 1 m. Hiện hồ chưa có nước nên anh Minh phải ra sông lấy nước. Mỗi lần ra sông anh gánh được 1 đôi nước đầy gồm 2 thùng hình trụ bằng nhau có bán kính đáy 0,2 m, chiều cao 0,4 m. a) Tính lượng nước (m3) anh Minh đổ vào hồ sau mỗi lần gánh (ghi kết quả làm tròn đến 2 chữ số thập phân). Biết trong quá trình gánh nước về thì lượng nước bị hao hụt khoảng 10% và công thức tính thể tích hình trụ là V=π⁢R2⁢h. b) Hỏi anh Minh phải gánh ít nhất bao nhiêu lần để đầy hồ? Bỏ qua thể tích thành hồ.

Bài 7. (1,0 điểm)

Sau buổi sinh hoạt ngoại khóa, nhóm bạn của Thư rủ nhau đi ăn kem ở một quán gần trường. Do quán mới khai trương nên có khuyến mãi, bắt đầu từ ly thứ 5 giá mỗi ly kem giảm 1 500 đồng so với giá ban đầu. Nhóm của Thư mua 9 ly kem với số tiền là 154 500 đồng. Hỏi giá của một ly kem ban đầu?

Bài 8. (3,0 điểm)

Cho đường tròn tâm O, bán kính R và điểm A nằm ngoài đường tròn sao cho OA > 2R. Từ A kẻ 2 tiếp tuyến AD ; AE đến đường tròn  ( O)  ( D ; E là 2 tiếp điểm). Lấy điểm M nằm trên cung nhỏ DE⏜  sao cho MD > ME. Tiếp tuyến của đường tròn (O) tại M cắt AD ; AE lần lượt tại I , J. Đường thẳng DE cắt OJ tại F.

a) Chứng minh: OJ là đường trung trực của đoạn thẳng ME và O⁢M⁢F^=O⁢E⁢F^ .

b) Chứng minh: tứ giác ODIM nội tiếp và 5 điểm I ; D ; O ; F ; M cùng nằm trên một đường tròn.

c) Chứng minh: J⁢O⁢M^=I⁢O⁢A^  và sin⁡I⁢O⁢A^=M⁢FI⁢O .

–HẾT–

Bộ Đề thi vào lớp 10 môn Toán TP.HCM năm 2020 có đáp án

Sở Giáo dục và Đào tạo TP.HCM

Kì thi tuyển sinh vào lớp 10

Năm học 2020

Môn thi: Toán (hệ Công lập)

Thời gian làm bài: 120 phút

Bài 1. (1,5 điểm)

          Cho parabol (P):y=-12⁢x2 và đường thẳng (d):y=x-4 .

a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P)  và (d)  bằng phép tính.

Bài 2. (1,0 điểm)

          Cho phương trình : x2-3⁢x-1=0  có hai nghiệm là x1,x2 .

Không giải phương trình, hãy tính giá trị của biểu thức : A=x1-1×2+1+x2-1×1+1 .

Bài 3. (0,75 điểm)

Quy tắc sau đây cho ta biết được ngày , tháng  năm 2019 là ngày thứ mấy trong tuần.

Đầu tiên, ta tính giá trị của biểu thức  ở đây được xác định bởi bảng sau:

Sau đó, lấy T chia cho 7 ta được số dư  r(0≤r≤6) . Nếu r = 0  thì ngày đó là ngày thứ Bảy. Nếu r = 1  thì ngày đó là ngày Chủ Nhật. Nếu r = 2  thì ngày đó là ngày thứ Hai. Nếu r = 3 thì ngày đó là ngày thứ Ba. … Nếu r = 6 thì ngày đó là ngày thứ Sáu. Ví dụ:   + Ngày 31/12/2019 có n=31,t=12;H=0⇒T=31+0=31;  số 31 chia cho 7 có số dư là 3, nên ngày đó là thứ Ba. a) Em hãy sử dụng quy tắc trên để xác định các ngày 02/9/2019 và 20/11/2019 là thứ mấy? b) Bạn Hằng tổ chức sinh nhật của mình trong tháng 10/2019. Hỏi sinh nhật của bạn Hằng là ngày mấy? Biết rằng ngày sinh nhật của Hằng là một bội số của 3 và là thứ Hai.

Bài 4. (0,75 điểm)

Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm (atmosphere). Bên dưới mặt nước, áp suất nước tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất y  (atm) và độ sâu x  (m) dưới mặt nước là một hàm số bậc nhất có dạng y = ax + b.

a) Xác định các hệ số a và b.

b) Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất 2,85 atm?

Bài 5. (1,0 điểm)

          Một nhóm gồm 31 bạn học sinh tổ chức một chuyến đi du lịch (chi phí chuyến đi được chia đều cho mỗi bạn tham gia). Sau khi đã hợp đồng xong, vào giờ chót có 3 bạn bận việc đột xuất không đi được nên họ không đóng tiền. Cả nhóm thống nhất mỗi bạn còn lại sẽ đóng thêm 18 000 đồng so với dự kiến ban đầu để bù lại cho 3 bạn không tham gia. Hỏi tổng chi phí chuyến đi là bao nhiêu?

Bài 6. (1,0 điểm)

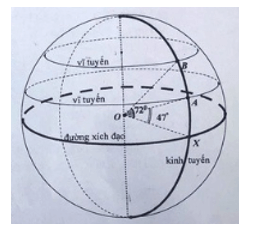
Cuối năm học, các bạn lớp 9A chia làm hai nhóm, mỗi nhóm chọn một khu vườn sinh thái ở Bắc bán cầu để tham quan. Khi mở hệ thống định vị GPS, họ phát hiện một sự trùng hợp khá thú vị là hai vị trí mà hai nhóm chọn đều nằm cùng trên một kinh tuyến và lần lượt ở các vĩ tuyến 47° và 72°.

a) Tính khoảng cách (làm tròn đến hàng trăm) giữa hai vị trí đó, biết rằng kinh tuyến là một cung tròn nối liền hai cực của trái đất và có độ dài khoảng 20 000 km.

b) Tính (làm tròn đến hàng trăm) độ dài bán kính và đường xích đạo của trái đất. Từ kết quả của bán kính (đã làm tròn), hãy tính thể tích của trái đất, biết rằng trái đất có dạng hình cầu và thể tích của hình cầu được tính theo công thức V=43⁢.3,14.R3 với R là bán kính hình cầu.

Bài 7. (1,0 điểm)

          Bạn Dũng trung bình tiêu thụ ca-lo cho mỗi phút bơi và 10 ca-lo cho mỗi phút chạy bộ. Hôm nay, Dũng mất 1,5 giờ cho cả hai hoạt động trên và tiêu thụ hết 1 200 ca-lo. Hỏi hôm nay, bạn Dũng mất bao nhiêu thời gian cho mỗi hoạt động?

Bài 8. (3,0 điểm)

          Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O) . Hai đường cao BD  và CD  của tam giác ABC  cắt nhau tại H . Đường thẳng AH  cắt BC  và (O)  lần lượt tại F  và  K (K≠A). Gọi L là hình chiếu D của  lên AB .

a) Chứng minh rằng tứ giác BEDC nội tiếp và D2=B⁢L.B⁢A .

b) Gọi J  là giao điểm của KD và (O), (J≠K).  Chứng minh B⁢J⁢L^=B⁢D⁢E^ .

c) Gọi I là giao điểm của BJ  và ED.  Chứng minh tứ giác ALIJ nội tiếp và I là trung điểm của ED .

–HẾT–